正相关样本下双指数分布位置参数的经验贝叶斯估计
黄金超,杨颖颖,郭 栋
(滁州职业技术学院 基础部,安徽 滁州 239000)
0 引 言
对单参数指数族未知参数的经验Bayes(EB)统计推断已有相当多的研究结果.如:基于独立同分布(iid)样本下,文献[1]~[4]讨论了单参数指数族EB估计和检验问题,并得到了一些有意义的结论;文献[5]~[6]在iid样本下分别讨论了双指数分布参数的EB检验和估计问题,但在相关样本下对双指数分布的参数EB估计问题没有进行相关讨论.在渗透理论、可靠性分析,以及某些多元分析等实际问题中,遇到的样本多具有相关性,常见的有正相关(PA)、负相关(NA).因此,在样本相关的情形下研究双指数分布参数的EB估计问题是非常有意义的.本文基于“平方损失”PA样本讨论双指数分布族数的EB估计,并构造一个渐近最优EB估计函数,在一定条件下获得的EB估计为渐近最优性,且收敛速度的阶为O(n-(rs-2)/2(s+2)),其中s>1,s∈N,1/2
下面给出PA样本随机变量(r.v.)序列的定义.
定义1随机变量X1,X2…,Xn称为正相关的(PA),如果对集合{1,2,…,n}任何两个不交的非空子集A1与A2都有:
Cov(f1(Xi,i∈A1),f2(Xj,j∈A2))≥0,
(1)
其中,f1和f2为任何两个使得协方差存在且对每个变元均非降或同时对每个变元均非升的函数,则称随机变量序列{Xj,j∈N}是正相关的(PA).如果对任何自然数n>2,X1,X2…,Xn都是正相关的(PA),则考虑如下双指数分布:
(2)
其中,x∈χ=(-∞,+∞),θ∈Ω=(-∞,+∞),Ω为位置参数空间.
与常见的指数分布族类似,双指数分布族是一类应用十分广泛的分布族.双指数分布族可用于构造保险精算模型,而各种经济模型经常构造双指数模型,双指数分布还用于工程技术.因此,在PA样本下研究双指数分布族位置参数的EB估计有着重要的理论与实践意义.
设G(θ)为参数θ的未知先验分布.随机度量X的边缘分布密度为:
(3)
其中,G(θ)为θ的未知先验分布.边缘分布函数记作F(x),即

(4)
取损失函数为:
L(θ,d)=(θ-d)2.
(5)
在平方损失式(5)下,θ的Bayes估计为:
(6)
其中,
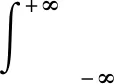

引理1[6]引理 1.1若f(x)>0,则θ的Bayes估计为:
其中,
(7)
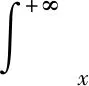
(8)
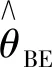
(9)

1 经验Bayes(EB)估计
设X1,X2,…,Xn和X为同分布PA样本,密度函数如式(3)所示.通常称X1,X2,…,Xn为历史样本,X为当前样本,令f(x)为X1的概率密度函数.本文假定:
f(x)∈CS,α,x∈R1,
(10)
其中,Cs,α为R1中一族概率密度函数,其s阶导数存在、连续,绝对值不超过α,且α为任意固定有界正数,s>1,s∈N.我们将
(11)
定义为F(x)的估计量,其中I[A]为A的示性函数.类似文献[6],定义g(x)的估计量为:
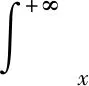
(12)
为估计f(x),引入核函数.令K(x)(r=0,1,…,s-1)为有界Borel可测函数,在(0,1)之外为0,且满足如下条件:
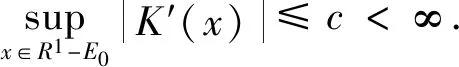
本文对PA序列的协方差作如下假定:
密度函数f(x)的核估计定义为:
(13)

定义θ的EB估计:
(14)
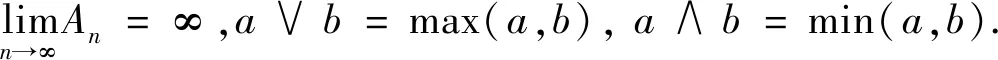
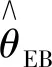
(15)

本文令c、c0、c1、c2…为不依赖n的正常数.
2 若干引理与主要结果
引理2[8]引理 1令X、Y是PA样本序列,且方差有限,则对任意的可微函数g1、g2有:
(16)
(17)
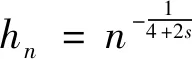
证明由Cr不等式可知:
(18)
由核函数性质可知:

(19)
由Taylor展开得:
(20)
将式(20)代入式(19)得:
(21)
由f(x)∈Cs,α和|K(t)|≤C可知:
当取hn=n-1/(2s+4)时,可知:
(22)
(23)
由|K2(v)|≤c,f(x)∈Cs,α可知:
(24)
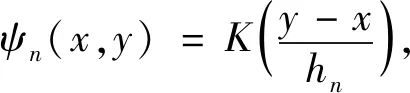
故由条件(D)和{Xn,n≥1}的弱平稳性可知:
(25)
所以,当hn=n-1/(2s+4)时,将式(24)和式(25)代入式(23)可得:
(26)
故有:
(27)
将式(22)和式(27)代入式(18)可得引理3的结论.

引理5[3]引理3对随机变量(Y,Z)和实数y,z≠0,0 证明由凸函数Jensen不等式可知: 引理7设g(x)和gn(x)分别由式(8)和式(12)定义,其中X1,X2…,Xn为PA样本序列,则对0 (28) 证明由定义(12),记 则 其中,Yi=ex-XiI[Xi>x]-eXi-xI[Xi≤x],Y1,Y2,…,Yn为PA样本序列,从而可知: (29) 所以,gn1(x)、gn2(x)分别为g1(x)、g2(x)的无偏估计.由Cr不等式可得: (30) 由Jensen不等式可知: (31) 其中, (32) 记φ(Xi)=Var[ex-XiI[Xi>x]],则 (33) 记g(x,y)=ex-yI[y>x],当x≠y时,g(x,y)为关于y可求偏导数,且 由引理2、条件(D)和{Xn,n≥1}的弱平稳性可知: (34) 将式(33)和式(34)代入式(32),再将式(32)代入式(31)可得: (35) 同理可证: (36) 将式(35)和式(36)代入式(30)引理得证. 则 (37) (Ⅰ)f(x)∈CS,α; 证明由引理4和条件(Ⅱ)可知: 故引理4的条件成立.因此,有: (38) 其中, 这里的I(x)为示性函数:I(x)=1,若x>0,否则I(x)=0. (39) 将式(39)代入A(n)可得: 由条件(Ⅱ)和(Ⅲ)可得: (40) (41) 将式(40)和式(41)代入式(38)可得: 取An=n1/2(s+2),可得: 易见: (Ⅰ)f(x)∈CS,α; 为第一类广义积分.而 由(Ⅰ)~(Ⅲ)式知,定理2的条件均满足. 本文在正相关(PA)样本下采用“平方损失”和密度函数核估计,研究双指数分布参数θ的经验Bayes (EB)估计问题,构造参数θ的 EB估计函数,并在适当的条件下证明了所提出的经验Bayes估计函数的渐近最优性,且收敛速度的阶为O(n-(rs-2)/2(s+2)),其中s>1,s∈N,1/2




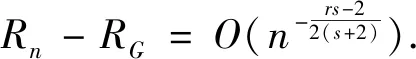
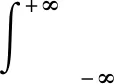



3 例 子


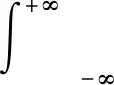

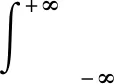
4 结 语

