第一类弱奇异Volterra积分方程解的渐近展开式

刘思靖, 王同科

(天津师范大学数学科学学院, 天津 300387)

1.引言

积分方程是近代数学的一个重要分支, 在数学、物理、力学中应用广泛[1-4].本文考虑第一类卷积核Volterra积分方程, 其形式如下

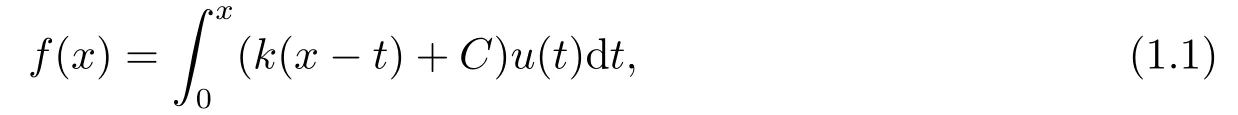
其中C为给定常数, 自由项f(x)和核函数k(x)已知.若k(x)中含有x−α,0<α<1或logx, 则方程(1.1)称为代数弱奇异或对数奇异Volterra积分方程.当核函数k(x) =x−α时, 该方程可转化为第二类Volterra积分方程, 其形式为[5]13

显然当C0时, 上式无法给出解的显式表达式.当k(x)=logx时, 其解为[5]13

其中γ=0.577216···为Euler常数(下同), 该解要求f′(0)存在, 且当x>0时,f(x)二阶可导.

积分方程可以用解析方法求解, 但仅对一些简单的方程有效, 如Polyanin等[5]给出了一些方程的解析解.更多的研究集中在方程的数值求解方面, 如HUANG等[6]使用Taylor展开对未知函数求和, 得到一个近似解; Mundewadi等[7]基于Hermite小波方法将Abel积分方程简化为代数方程求解; XIANG[8]使用Laplace变换导出带有高振荡核的Volterra积分方程解的表达式, 并利用Clenshaw-Curtis-Filon型方法求其近似解; YANG[9]通过Laplace变换将奇异的Volterra积分方程转化为代数方程, 结合Taylor展式及Laplace逆变换求出数值解.需要指出的是, Laplace变换作为一个重要的数学工具, 在各类线性微分和积分方程的求解中起着重要作用, 其难点在于逆变换的计算.

本文考虑自由项f(x)在x=0点含有代数和对数奇性, 并在此处成立以下的级数展开式

在(1.2)式中若αk取值为实数(包括无理数), 则称此级数为psi级数[10]; 若αk取值仅为有理数,称此级数为Puiseux级数[11].本文考虑αk为实数的一般情形.我们通过Laplace变换导出积分方程(1.1)的解在零点及无穷远点(仅对核函数代数奇异情形)渐近展开式的一般形式, 其在零点的展开式可以作为方程(1.1)当x比较小时的近似解; 其在无穷远点的展开式可以作为方程(1.1)当x比较大时的近似解.对这些展开式做Pad逼近[2]还可以提高近似解的精度.最后给出实例来说明展开式的正确性以及本文方法的有效性.

2.Laplace变换及其逆变换

本节为预备知识, 给出Laplace变换及其逆变换的各种类型渐近展开式.

定义1给定一个函数f(x), 它的Laplace变换定义为

其逆变换为[12]

引理1[13]设f(x)在零点存在形如(1.2)的psi级数展开式, 其中αk(k= 1,2,3,···)为实数,满足−1<α1<α2<···→∞,σk,j为非负整数.则F(s)在无穷远点的psi级数展开式为

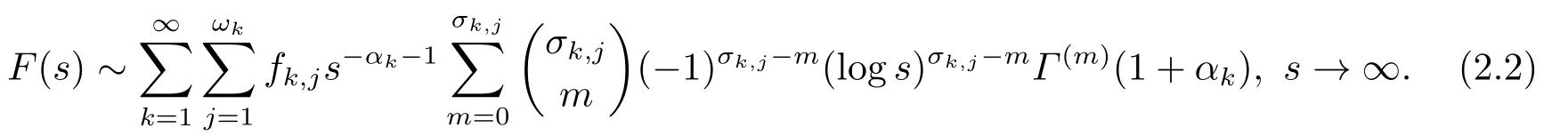
引理2[11]设F(s)在无穷远点成立psi级数展开式

(i) 若βk为实数, 并满足0< β1< β2< ··· →∞,µk,j为非负整数, 则F(s)的Laplace逆变换f(x)在x=0点的展开式为

(ii) 若βk(k=1,2,···)为实数, 并满足0≤β1<β2<···→∞,µk,j为负整数, 则

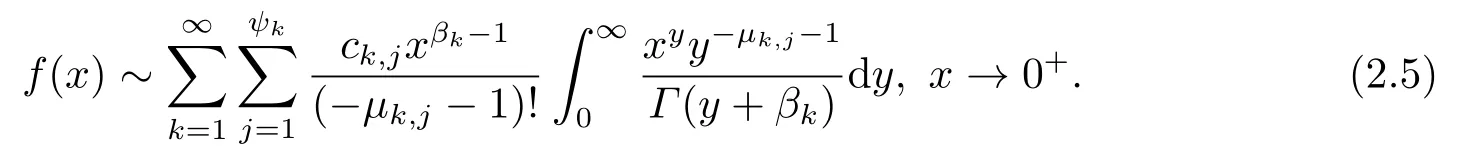
引理3[13]设F(s)当s →∞时一致趋向于0, 其在s=0点的psi级数展开式为

其中γk(k= 1,2,···)为实数并满足−N0< γ1< γ2< ··· →∞,ρk,j及N0为非负整数.进一步假设F(s)含有非零奇点si(i=1,2,··· ,M), 且成立如下的Laurent级数展开式

其中vi ≥0(i=1,2,··· ,M).则F(s)的逆变换f(x)在x=∞点具有如下形式的psi级数展开式

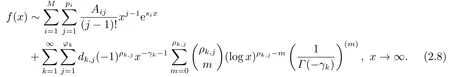
引理4设β ≥0, b为任意实数,λ为非负整数, 则有

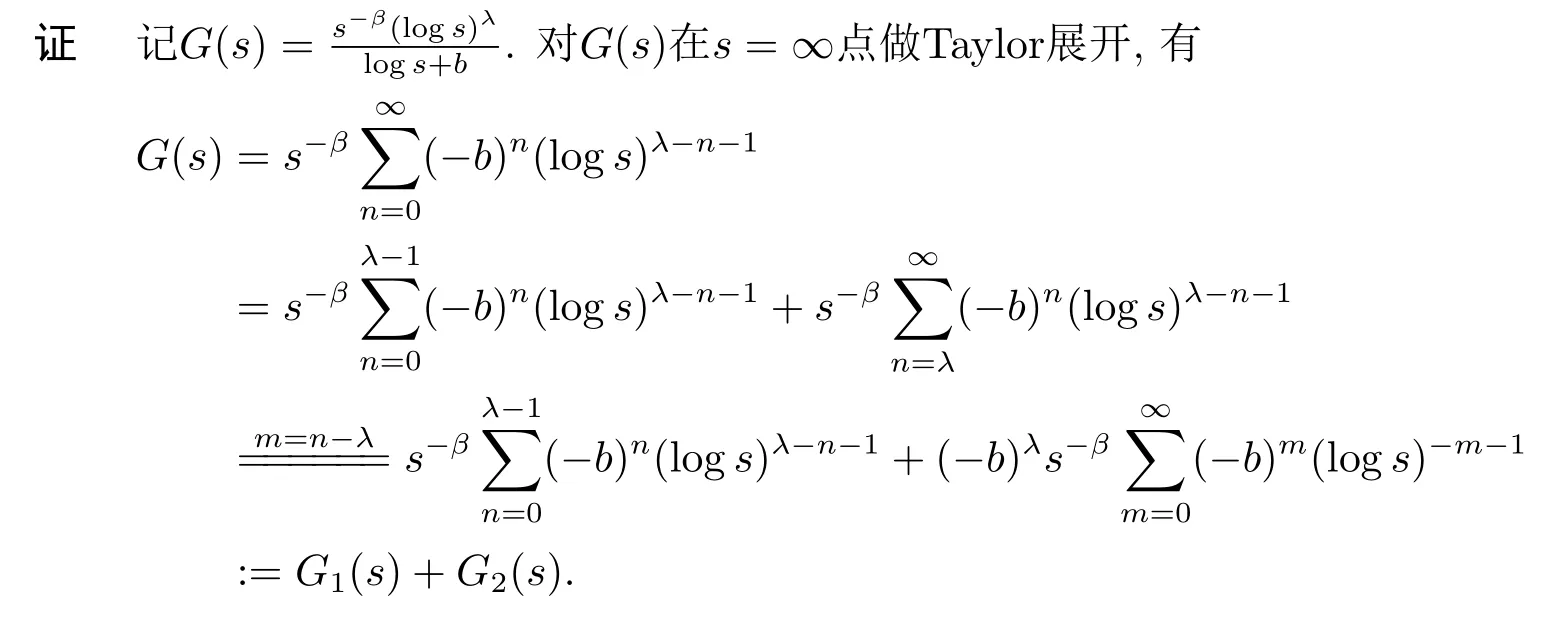
应用(2.5)式对G2(s)进行Laplace逆变换, 可得

再对G1(s)应用(2.4)式, 可知(2.9)式成立.

3.方程解的渐近展开式

对积分方程(1.1)两边作用Laplace变换, 应用卷积定理[12], 得

其中U(s) =L[u(x)],K(s) =L[k(x)],F(s) =L[f(x)].显然对U(s)求逆可得方程(1.1)的精确解u(x), 但通常情况下难以实现.下面针对一些重要的核函数求u(x)在零点和无穷远点的渐近展开式.

我们先求解在零点的渐近展开式.设f(x)在零点的psi级数为(1.2)式, 则其Laplace变换F(s)在无穷远点的psi级数为(2.2)式.当k(x)=x−αlogµx,0<α<1,µ为非负整数时, 有[13]

则由(2.2)式

对于这种一般情形,可以由数学软件求出U(s)在s=∞点的有限项级数展开式,进而由引理2或引理4求出u(x)在x=0点的有限项psi级数展开式, 下面讨论三种常用的重要情形.

(I)µ=0的情形

定理1设f(x)在零点的psi级数为(1.2)式, 且k(x)=x−α, 则方程(1.1)的解u(x)在x=0点的psi级数展开式为

证 当k(x)=x−α时,K(s)=Γ(1−α)sα−1.当s →∞时, 有

则U(s)在s=∞点的展开式为

则由引理2(i)可知, 积分方程(1.1)的解u(x)在x=0点的psi级数展开式为(3.3)式.

(II)α=0, µ=1的情形

定理2设f(x)在零点的psi级数为(1.2)式, 且k(x)=logx, 则方程(1.1)的解u(x)在x=0点的psi级数展开式为

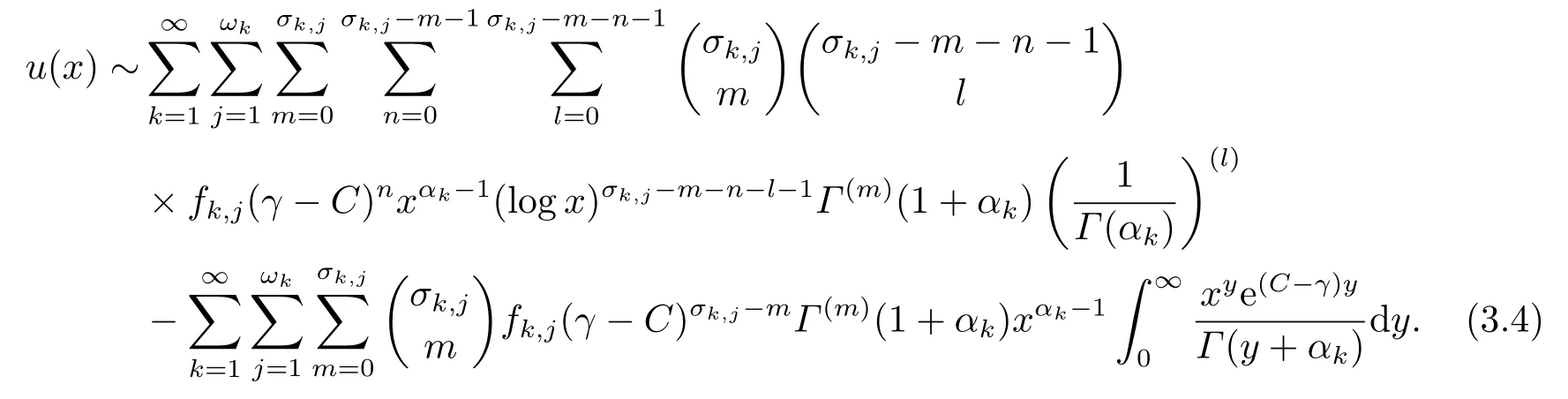
证当k(x) = logx时,K(s) =−s−1(logs+γ).则sK(s)+C=−(logs+γ −C), 从而U(s)在s=∞点可展开为

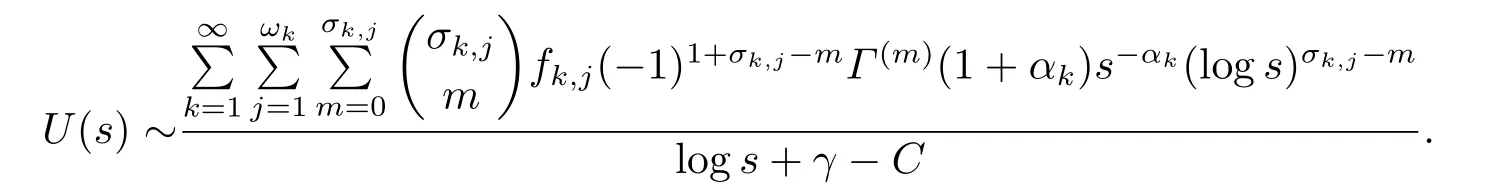
则由引理4可知, 积分方程(1.1)的解u(x)在x=0点的psi级数展开式为(3.4)式.

(III) 0<α<1, µ=1, C=0的情形

定理3设f(x)在零点的psi级数为(1.2)式, 且k(x) =x−αlogx, 则方程(1.1)(C= 0)的解u(x)在x=0点的psi级数展开式为

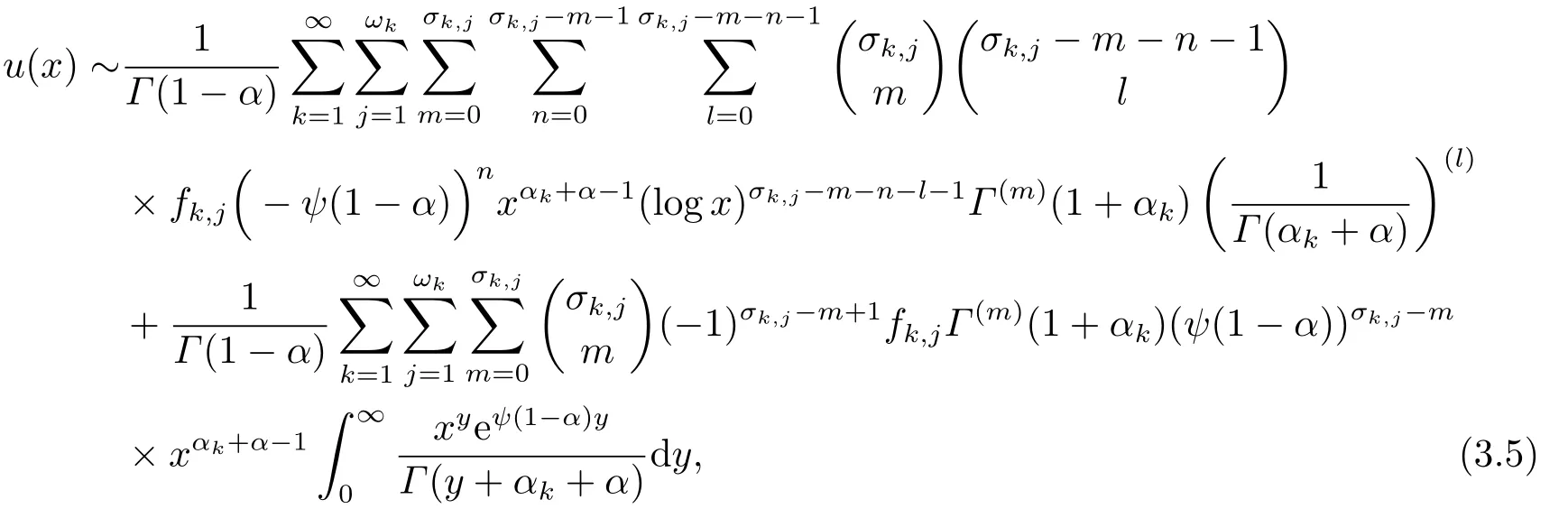
其中ψ(1−α)=Γ′(1−α)/Γ(1−α).

证当k(x)=x−αlogx时,K(s)=sα−1(Γ′(1−α)−Γ(1−α)logs).从而U(s)在s=∞点可展开为

则由引理4可知, 积分方程(1.1)的解u(x)在x=0点的psi级数展开式为(3.5)式.

由于我们假定f(x)在零点具有一般形式的psi级数展开式, 所以u(x)在x= 0点的展开式非常复杂.若f(x)不包含对数项, 即则(3.3)、(3.4)和(3.5)式可分别化简为

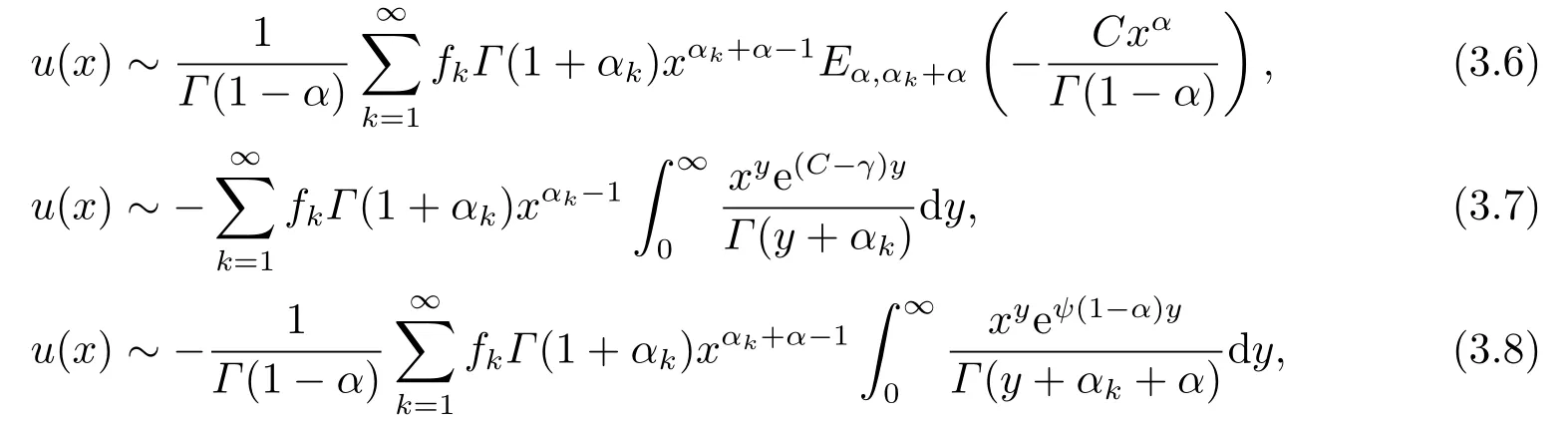
其中(3.6)式中的Mittag-Leffier函数En1,n2(z)定义为

注1Linz[14]仅给出了(3.6)式中的第一项, 此处我们给出了方程的解在x= 0点的无穷项级数展开式.由(3.3)和(3.6)知, 只要f(0)= 0(对应α1= 0), 则方程(1.1)的解u(x)在x= 0点一定奇异, 而这种奇异性质完全由(3.3)和(3.6)式刻画出来.在设计数值算法时, 我们应当考虑解的这种奇异性质.

注2若f(x)在零点的展开式为有限项, 则(3.4)和(3.7)式即为方程(1.1)的精确解.例如取f(x)=1,C=1, 则方程(1.1)为

由(3.7)式可得

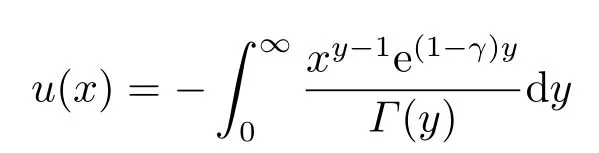
为方程(3.9)的精确解.

本小节针对三种常见的核函数给出了积分方程(1.1)的解在零点的渐近展开式, 这些展开式显式地给出了u(x)与f(x)之间的依赖关系, 刻画了u(x)在x= 0点的奇异性质.注意到(3.4)和(3.7)的展开式中含有特殊形式的无穷积分, 当C −γ <0时, 可通过Gauss-Laguerre求积公式来计算.

方程(1.1)的解在x= 0点的渐近展开式当x比较小时有比较高的精度, 通常我们仅取解的有限项级数展开式, 记为up,0(x).为了扩大级数的收敛域, 我们进一步求出up,0(x)的Pad逼近,记为ur,0(x).为了检验级数的逼近效果, 定义误差函数

让x由小变大通过计算一些eξ,0(x), 来判断级数解的逼近精度.

下面我们推导方程的解在无穷远点的渐近展开式, 只考虑µ=0和0<α<1的情形.

定理4设F(s)当s →∞时一致趋向于0, 且在零点的psi级数为(2.6)式.对于核k(x) =x−α, 考虑以下几种情形.

(I)F(s)除s=0外无其它奇点.

(i)C=0, 积分方程(1.1)的解在x=∞点的psi级数展开式为

(ii)C >0, 积分方程(1.1)的解在x=∞点的psi级数展开式为

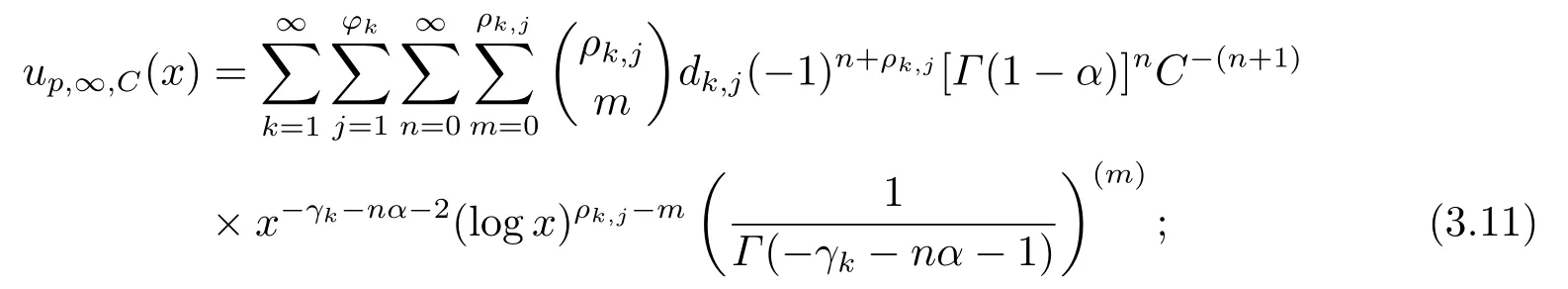
(iii)C <0, 积分方程(1.1)的解u(x)在x=∞点的psi级数展开式为

(II)F(s)有其它奇点, 形如(2.7)式.此时, 记h(s)=

(i)C ≥0, 积分方程(1.1)的解u(x)在x=∞点的psi级数展开式为

(ii)C <0, 积分方程(1.1)的解u(x)在x=∞点的psi级数展开式为

证当k(x)=x−α时,K(s)=Γ(1−α)sα−1.当s →0时, 若C=0, 则有

(I)(i)当F(s)除s=0点外无其它奇点,且C=0时,U(s)除s=0点外无其它奇点.由(3.1)式可知U(s)在s=0点的展开式为

由引理3可得u(x)在x=∞点的psi级数展开式up,∞,0(x), 如(3.10)式所示.

(I)(ii) 当F(s)除s= 0点外无其它奇点, 且C >0时,U(s)除s= 0点外无其它奇点.由(3.15)知U(s)在零点的展开式为

由引理3可得u(x)在x=∞点的psi级数展开式up,∞,C(x), 如(3.11)式所示.

(II)(ii) 当F(s)有非零奇点, 且C <0时,U(s)有奇点si(i= 0,1,··· ,M).不妨设U(s)的这M+1个奇点互异,其中s0为sK(s)+C的零点.则直接计算可得U(s)在s=s0点的Laurent级数展开式为

其中v0≥0为整数.将h(s)在si(i=1,2,··· ,M)点做Taylor展开, 有

由U(s)=F(s)h(s), 可得U(s)在s=si点的Laurent级数展开式为

其中vi ≥0为整数.分别对上述展开式做Laplace逆变换, 可得

注意到U(s)在零点的级数展开式仍为(3.16), 由引理3可知u(x)在x=∞点的级数展开式为up,∞,C(x)+us0(x)+即展开式(3.14)成立.其它情形显然成立.本节针对一些核函数求出了方程(1.1)的解在零点及无穷远点的psi级数展开式, 对于这些级数展开式进行收敛性分析是一项非常困难的工作.目前已知Hemmi等[10]针对非线性常微分方程的psi级数解讨论了收敛性.正如Olver[15]所言: 不管函数的渐近展开式是否收敛, 它们都可以在数值计算中发挥重要作用.一般来说, 我们应当使用交叉验证的方法判断这些级数的精度.例如, 对于解在零点的渐近展开式通过定义误差函数可以得到级数解的有效范围; 再如, 对于解在无穷远点的渐近展开式, 如果它和解在零点的展开式在某一个有限区间内匹配很好, 则可以认为两个展开式都正确, 而且x越大, 该展开式的逼近越精确.另外, 我们还可以使用数值方法来检验两种形式的渐近展开式的正确性和有效性.

4.数值算例

本节给出几个算例说明解的渐近展开式的正确性及有效性.

例1考虑第一类线性弱奇异Volterra积分方程

其精确解可由数学软件求出, 但表达式很复杂, 不再给出.对方程(4.1)进行Laplace变换, 得

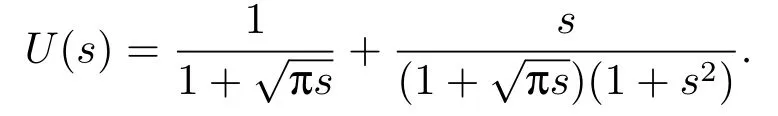
将U(s)在s=∞点进行级数展开, 由定理1或(3.6)式, 可得到u(x)在x=0点的psi级数展开式为

由此可知, 解u(x)在x= 0点弱奇异.由于U(s)有两个一阶极点s1= i和s2=−i, 分别将U(s)在这两点做Laurent级数展开, 可得

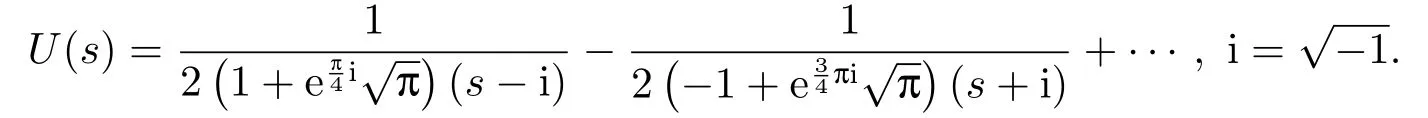
进一步将U(s)在s=0点进行级数展开, 由定理4, 可得u(x)在x=∞点的psi级数展开式为

对up,0(x)取到x30, 对up,∞(x)取到1/x10, 并对它们分别做Pad逼近, 结果为

对上述四个展开式up,i(x),ur,i(x)(i= 0,∞)分别在(0,200]上绘制绝对误差对数图形, 如图1所示, 其中ei= log10|u(x)−up,i(x)|;er,i= log10|u(x)−ur,i(x)|, i= 0,∞.从图1可以看出, 当x足够小时, 展开式up,0(x)及ur,0(x)都有着很高的精度; 当x逐渐增大时, 展开式up,∞(x)及ur,∞(x)的精度逐渐提高.尽管在零点及无穷远点的级数展开式及Pad逼近式的精度都很高, 但我们发现在图1左右两图中交点的误差还是Pad逼近后的精度高于原级数,这说明我们所做的Pad逼近能够提高级数的逼近精度, 并且由此我们还得到例1的解在全区间(0,∞)上的级数展开式, 即当x ≤9时, 用ur,0(x)近似u(x); 当x>9时, 用ur,∞(x)近似u(x), 则总体逼近精度可达到10−5量级.

图1 例1解的展开式绝对误差对数图形

例2考虑第一类线性弱奇异Volterra积分方程

由定理1, 可得到u(x)在x=0点的psi级数展开式为

在上式中n取到21, 求其Pad逼近, 得

由up,0(x)和ur,0(x)的表达式知该方程的解在x=0点代数且对数奇异.

由于U(s)有一个一阶极点则由定理4, 可得u(x)在x=∞点的psi级数展开式为

在上式中n取到10, 并进一步求出u(x)在x=∞点的Pad逼近式

本例无法求出精确解, 我们通过对Laplace变换U(s)在区间(0,90]上进行数值结果比对,部分结果在表1中列出, 其中uc(x)代表Laplace逆变换数值解, 由固定Talbot方法[16]得到.在表1中eξ,0=|uc(x)−uξ,0(x)|;reξ,∞=|uc(x)−uξ,∞(x)|/|uc(x)|, ξ=p,r.由于该问题的解不稳定, 当x足够大时, 数值增长很快, 我们取相对误差来估计精度.从表1可以看出, 当x足够小时,up,0(x)与Pad逼近ur,0(x)都有较高的精度, 还可发现Pad逼近ur,0(x)不但精度高而且收敛范围较大; 当x逐渐增大时,up,∞(x)与ur,∞(x)的精度逐渐提高, 但仍发现Pad逼近ur,∞(x)精度相对更高.从表1中还可发现当x= 20时,ur,0(20) 与ur,∞(20) 的精度接近, 均在10−7量级.由此可知, 当x ≤20时, 用ur,0(x)计算, 当x >20 时, 用ur,∞(x)计算, 则可得到在全区间(0,∞)上至少具有10−7精度的近似解表达式.

表1 例2计算结果对比

例3取f(x) =其中K0(x)为第二类零阶变形Bessel函数, 其在x= 0点的级数展开式为

考虑两种核函数k1(x)=logx,C1=1/2和k2(x)=x−1/2logx,C2=0.方程(1.1)可写为

对方程(4.3)进行Laplace变换, 得

上式中K(y), E(y)分别为第一类和第二类完全椭圆积分, 定义为

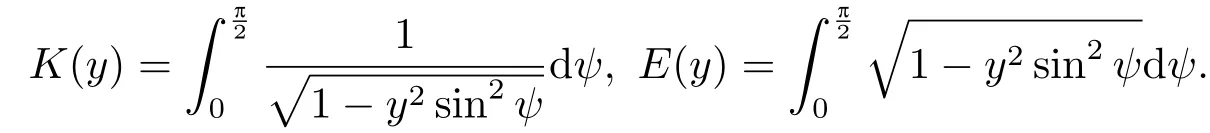
直接由Mathematica对Ui(s)(i=1,2)在s=∞点进行级数展开, 得

则由定理2和定理3可得ui(x)(i=1,2)在x=0点的展开式前几项为

定义误差函数ep,i(x) = log10|uc,i(x)−up,i(x)|, i= 1,2, 其中uc,i(x)代表Laplace逆变换数值解, 由固定Talbot方法[16]得到.对上述误差函数在(0,4]内绘图, 如图2所示.由图2可知展开式up,i(x)(i= 1,2)在零点附近具有很高的精度, 但随着x的增大展开式的精度逐渐下降, 需使用数值方法求解.由于此时已经分离出解的奇性, 利用该展开式, 高精度数值算法的设计将更加容易.

图2 例3展开式up,i(x)(i=1,2)的绝对误差对数图形

5.总结

本文对于第一类线性弱奇异Volterra积分方程, 用Laplace变换方法研究解在零点及无穷远点(仅对代数奇异核)的渐近展开式.这些展开式的作用体现在两个方面, 一是揭示了方程的解在零点及无穷远点的渐近性质; 二是这些展开式可以作为方程的解当自变量变小或变大时的近似解.最后通过一些例子说明了展开式的正确性和有效性.相比于其它求解方法, 本文方法不仅可以分离出解的奇异部分, 还可能在部分问题的计算中得到方程在全区间上的近似解.