轨迹法在解不定三角形问题中的应用
安徽省芜湖市第一中学 刘海涛 (邮编:241000)
在一轮复习的教学中,发现一些以解不定三角形为背景的取值范围或最值问题中,若考虑构造三角函数解题,往往计算量大,过程繁杂,学生容易出错,而从动点的轨迹方面入手,数形结合分析问题,可以巧妙求解,避免繁杂的运算过程,起到事半功倍的解题效果.下面通过八道解不定三角形问题,谈轨迹法在解不定三角形中的应用.
1 轨迹为线段模型
例1已知M是锐角△ABC的边AB上一点则AB的取值范围是_____.
解析在△ACM中,由余弦定理得AM2=CM2+AC2-2·CM·ACcos∠ACM=72,即,由正弦定理得,即如图1,过点C作CE⊥AB于点E,作CF⊥AC交AB于点F,由题不难明白点B的轨迹是线段EF(不含端点E、F),则AE<AB<AF.易知△ACE是以AC为底边的等腰直角三角形,△ACF是以AF为底边的等腰直角三角形,所以AE=综 上 ,得
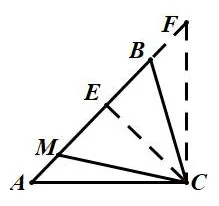
图1
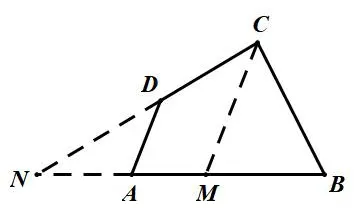
图图22
评注解答该题的关键是抓住锐角三角形这一条件,分别作出B、C为直角顶点的临界情况(以AC为底边的等腰直角△ACE,以AF为底边的等腰直角△ACF),得到点B的轨迹是线段EF(不含端点E、F),进而得到AE<AB<AF.
例2在平面四边形ABCD中,∠A=∠B=∠C=75o,BC=2,则AB的取值范围是______.
解析如图2,过点C作CM//DA交AB于点M,分别延长CD、BA交于点N,则可以理解为点A的轨迹是线段MN(不含端点M、N),则BM<AB<BN.在△BCN中,由正弦定理得即在 △BCM中,由正弦定理得即
评注从动点的轨迹入手,深入分析题目中四边形的结构特征,找到点A的运动轨迹为线段MN(不含端点M、N),分别分析点A位于M、N两点的临界情况,从而确定取值范围.该题也可以利用对角线AC将四边形分割为两三角形,将问题转化为关于∠BAC的三角函数,但是计算量大,过程复杂.
2 轨迹为外接圆模型
例3已知△ABC中则△ABC面积的最大值为____.
解析设△ABC的外接圆半径为R,由正弦定理,得即R=1.设边BC上的高为h,则如图3,圆O为△ABC的外接圆,点A的轨迹为优弧BC(不包含B、C两端点),显然当点A位于优弧BC的中点时,h取最大值为1+所以△ABC面积的最大值为
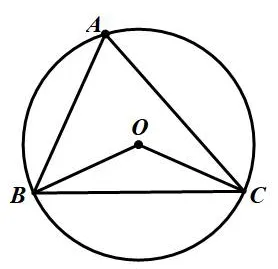
图3
评注利用外接圆找到动点A的轨迹为圆弧,数形结合,知点A位于优弧BC的中点时取到面积的最大值,解答过程巧妙自然容易理解掌握.该题也可以运用函数思想构造函数解题,得到再求出最大值,但是该法运算量大,容易出错.
例4已知锐角△ABC的内角A、B、C的对边分别为a、b、c,若则bc的取值范围是____.
解析设△ABC的外接圆半径为R,由正弦定理,得即R=1.如图4,圆O为△ABC的外接圆,A1C、A2B均为圆O的直径,则,则点A的轨迹为劣弧A1A2(不包含A1、A2两端点),数形结合不难明白动点A从点A1向点A2运动的过程中,边c长度递增,边b长度递减.在直角△A1BC中 ,b=2,c=1,则b-c=1;在 直 角△A2BC中,b=1,c=2,则b-c=-1.综上bc∈ (-1,1 ).
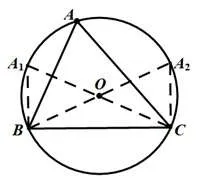
图4
评注相较于例3,例4中的三角形要求为锐角三角形,通过外接圆考虑角B、C分别是直角的临界情况,得到动点A的轨迹,数形结合分析点A运动的过程中边b、c的变化情况,问题迎刃而解,过程简捷,避免了繁杂的计算.
3 轨迹为隐圆模型
例5已知△ABC中BC=2,AB=AC,则△ABC面积的最大值为____.
解析如图5,以线段BC所在直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系xOy,则B(-1,0),C(1,0).设A(x,y)(y≠0),由AB=AC,得整 理 得 (x-2)2+y2=3,则点A的轨迹是以点(2,0)为圆心为半径的圆(除去与x轴的两个交点),则≤,故△ABC面积的最大值为.
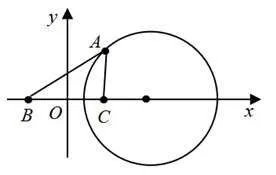
图5
评注该题看似与解析几何无关,实则为隐圆(阿波罗尼斯圆)问题,若解题时能看破这一点,建立坐标系则可轻松解题,省去繁杂的计算.该题也可以设AC=b,建立面积关于b的函数求解,但过程复杂,运算量大.
例6已知△ABC的内角A、B、C的对边分别为a、b、c,若a2+2b2+2c2=8,则 △ABC面积的最大值为____.
解析如图6,以点B为坐标原点,BC所在直线为x轴,建立平面直角坐标系xBy,则B(0,0),C(a,0),设A(x,y),由 题 得a2+2(x2+y2)+2(x-a)2+y2=8,整理得数形结合,有S△ABC=当且仅当,即
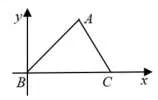
图6
评注首先固定边BC,将A视作定点,由条件式得为定值,发现该题的本质是隐圆问题,于是借助坐标系得出动点A的轨迹方程,轻松得出面积的最值.关于隐圆问题,在文献[1]和[2]中做了详细的介绍,读者可参考.
4 轨迹为椭圆模型
例7已知△ABC的周长为18,BC=8,则△ABC内切圆半径r的最大值为____.
解析容易知道S△ABC由题知AB+AC=18-8=10>BC,由椭圆的定义知,点A的轨迹为以B、C两点为焦点,10为长轴长的椭圆(除去椭圆长轴两端点).如图7,以线段BC所在直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系xOy,则点A的轨迹为轨迹方程为数形结合,知点A位于短轴端点时,S△ABC取最大值为
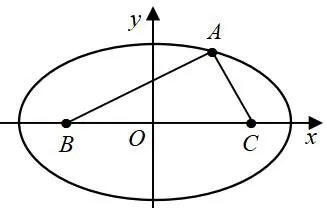
图7
评注首先通过S△ABC=9r将问题转化为三角形面积最大值问题,由条件不难发现AB+AC=10>BC,进而得到点A的轨迹为椭圆,数形结合便可得到答案.另外该题也用海伦公式S=将三角形面积转化为关于边b(或c)的函数求最大值.
例8已知△ABO(O为坐标原点)的重心、内心分别是G、I,且则cos∠OAB的最小值为____.
解析设A(x,y)(y≠0),则由得点I的横坐标为,又I为 △ABO的内心,所以=8>||
OB,由椭圆定义知点A的轨迹为以O、B为焦点的椭圆(除去长轴两端点),如图8,由椭圆的几何性质已知点A位于短轴端点时∠OAB取最大值,此时△ABO为等边三角形,则cos∠OAB的最小值为
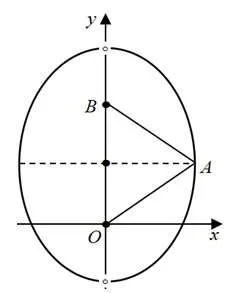
图8
评注该题是一道内涵丰富的解三角形问题,考查了重心、内心等性质,解答该题的关键在于得到|AB|+|AO|=8为定值,由椭圆定义知动点A的轨迹为椭圆,利用椭圆性质解答该题省去繁杂的计算过程,巧妙简捷.
以上8道求取值范围或最值问题,是笔者在一轮复习中为学生准备的解不定三角形例题,旨在帮助学生建立从动点轨迹的角度分析问题的解题意识,学会从不同角度思考问题,发散解题思维,形成解题策略,提高解题能力,发展数学核心素养[3].

