导数与三角“交会型”试题演绎出来的精彩

巨小鹏

(陕西省汉中市龙岗学校)

作为高考压轴题,承担着选拔人才功能的导数与三角函数结合的试题,能考查学生综合能力和素养.新高考的考查已经不仅仅局限于基本知识和基本技能,更重视对学生综合核心素养和关键能力的考查,题目会更加灵活多变,富有创新性和综合性.在有限的题目里融入数学文化、生活实际,那么知识之间的融合必然会更加精彩,将不同的知识点融合交会,提高了难度,也考查了学生的综合素养.导数与三角函数的精彩交会将是继指数函数、对幂函数综合交会之后的又一题型,于是周期性、有界性和放缩就被融入进来,在这个过程中,单调性、最值、极值、零点、取值范围、恒成立和证明不等式等成了精彩交会的热点.

1 恒成立问题

不等式恒成立问题常见方法:1)分离参数a≤f(x)恒成立(a≤fmin(x))或a≥f(x)恒成立(a≥fmax(x));2)数形结合;3)讨论最值fmin(x)≥0或fmax(x)≤0恒成立;4)直接讨论参数.

例1(2015 年湖南卷文21)已知a＞0,函数f(x)＝aexcosx(x∈[0,＋∞),记xn为f(x)从小到大的第n(n∈N*)个极值点.

(1)证明:数列{f(xn)}是等比数列;

(2)若对一切n∈N*,xn≤|f(xn)|恒成立,求a的取值范围.

在解决数列与函数的综合问题时,如果是证明题,要根据数列的定义明确证明的方向,如果是不等式恒成立问题,要使用不等式恒成立的各种不同解法(如变量分离法、最值法、因式分解法等)进行求解.总之解决这类问题要把数列看作特殊函数,并把它和不等式的知识巧妙结合起来综合处理.

2 不等式证明问题

例2(2020年全国Ⅱ卷理21)已知函数f(x)＝sin2xsin2x.

(1)讨论f(x)在区间(0,π)的单调性;

(2)证明:|f(x)|≤

(3)设n∈N*,证明:

(3)结合(2)的结论有

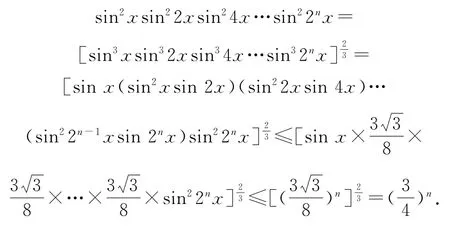
导数是研究函数的单调性、极值(最值)有效的工具,而函数是高中数学中重要的知识,对导数应用的考查主要从以下几个角度进行:1)导数的几何意义,往往与解析几何、微积分相联系;2)利用导数求函数的单调区间,判断单调性或根据单调性求参数;3)利用导数求函数的最值(极值),解决生活中的优化问题;4)考查数形结合思想的应用.

例3(2019 年天津卷理20)设函数f(x)＝excosx,g(x)为f(x)的导函数.

(1)求f(x)的单调区间;

(2)当x∈]时,证明:

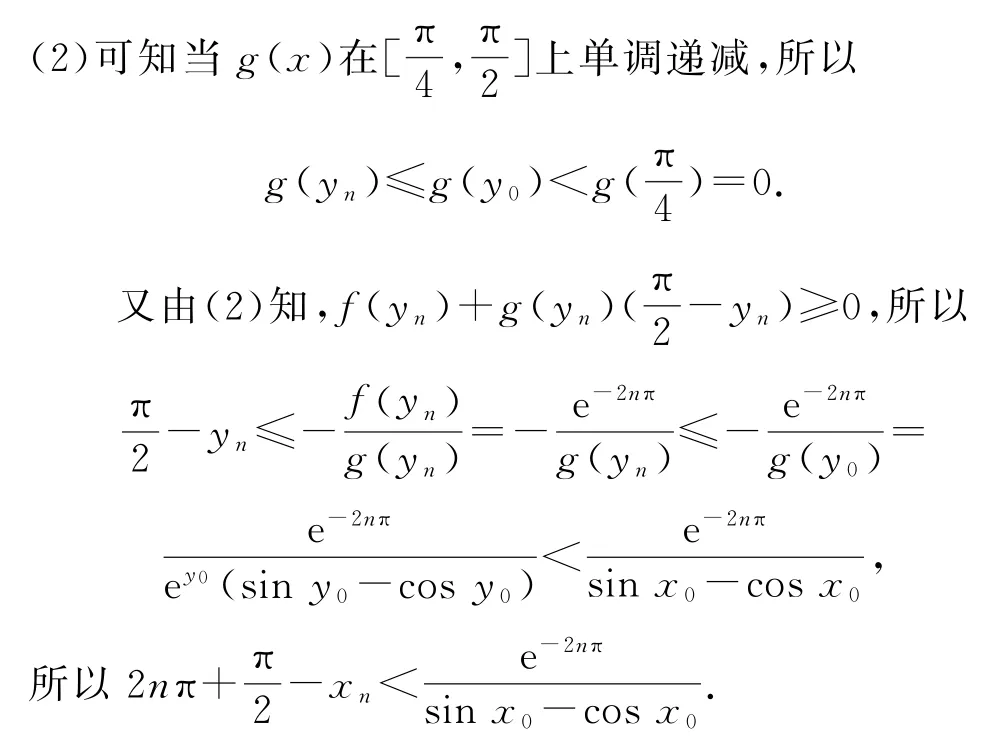
1)利用导数证明不等式或解决不等式恒成立问题关键是把不等式变形后构造恰当的函数,然后用导数判断该函数的单调性或求出最值,以达到证明不等式的目的;2)利用导数解决不等式恒成立问题,应特别注意区间端点是否能取到;3)学会观察不等式与函数的内在联系,学会变主元构造函数,再利用导数证明不等式.

3 极值问题

例4(2017年山东卷理20)已知函数f(x)＝x2＋2cosx,g(x)＝ex(cosx－sinx＋2x－2),其中e＝2.71828…是自然对数的底数.

(1)求曲线y＝f(x)在点(π,f(π))处的切线方程;

(2)令h(x)＝g(x)－af(x)(a∈R),讨论h(x)的单调性并判断有无极值,有极值时求出极值.

(1)y＝2πx－π2－2(求解过程略).

(2)由题意可得

则h′(x)＝2(ex－a)(x－sinx),令m(x)＝x－sinx,则m′(x)＝1－cosx≥0,所以m(x)在R 上单调递增.又因为m(0)＝0,所以当x＞0 时,m(x)＞0,当x＜0时,m(x)＜0.

当a≤0时,ex－a＞0.若x＜0,h′(x)＜0,h(x)单调递减;若x＞0,h′(x)＞0,h(x)单调递增,所以当x＝0时,h(x)取得极小值h(0)＝－2a－1.

当a＞0时,由h′(x)＝0,得x1＝lna,x2＝0.

当0＜a＜1时,lna＜0,当x∈(－∞,lna)时,h(x)单调递增;当x∈(lna,0)时,h(x)单调递减;当x∈(0,＋∞)时,h(x)单调递增,所以h(x)极大值为h(lna)＝－a[ln2a－2lna＋sin(lna)＋cos(lna)＋2],极小值为h(0)＝－2a－1.

当a＝1 时,lna＝0,所以h(x)在R 上单调递增,无极值.

当a＞1时,lna＞0,同理,当x＝0时,h(x)取得极大值h(0)＝－2a－1,h(x)取得极小值h(lna)＝－a[ln2a－2lna＋sin(lna)＋cos(lna)＋2].

此题考查导数的几何意义、应用导数研究函数的单调性与极值、分类讨论思想.恰当分类讨论是关键,当一次求导不能解决问题时,可以再次求导.易错点是分类讨论不全面、不彻底、不恰当,或对复杂式子变形能力差,从而造成不能完整解答出来.

4 零点问题

对函数零点的考查主要有验证零点的存在性、判断零点的个数以及已知零点个数求参数的取值范围.

例5(2019年全国Ⅰ卷文20)已知函数

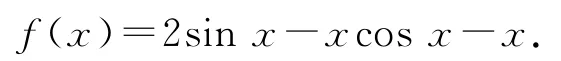
(1)证明:f′(x)在区间(0,π)存在唯一零点;

(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.

综上,f′(x)在区间(0,π)存在唯一零点.

(2)方法1若x∈[0,π]时,f(x)≥ax,令

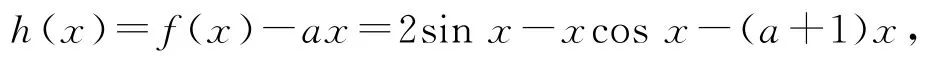
则h′(x)＝cosx＋xsinx－1－a,由(1)可知,

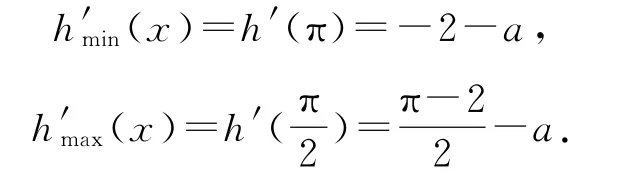
当a≤－2 时,h(x)在[0,π]上单调递增,所以h(x)≥h(0)＝0,此时f(x)＞ax恒成立.

综上,a的取值范围为(－∞,0].

方法2由(1)可知,f′(x)在区间(0,π)存在唯一零点,设为x0,则f(x)在(0,x0)上单调递增,在(x0,0)上单调递减.又因为f(0)＝0,f(π)＝0,所以当0≤x≤π时,f(x)≥0,又当a≤0,0≤x≤π 时,ax≤0,故f(x)≥ax;当a＞0 时,f(π)＝0≤aπ,f(x)≥aπ不恒成立.

综上,a取值范围为(－∞,0].

本题利用导数讨论函数零点个数、根据恒成立的不等式求解参数范围.对于此类端点值恰为恒成立不等式取等的问题,通法是采用构造函数的方式,将问题转变成求函数的最值,进而通过导函数的正负来确定所构造函数的单调性,从而得到最值.结合第(1)问的结论分析不等式结构,往往会有出其不意的结果,比如方法2,利用必要性探路,先猜后证,避免了分类讨论.我们发现通法中分类讨论是通法必不可少的,原因就在于三角函数具有周期性和有界性.

三角函数与指数函数、对数函数、幂函数等综合的问题,难点在于三角函数求导后依然是三角函数.除了以上几种类型,还有已知极值点或者零点(个数)求参数取值范围问题、零点不存在问题、最值问题等.这些题看似是由不同的函数进行融合,但可以利用导数的优越性、三角函数的特殊性对函数的性质进行再次研究,其实最终还是万变不离其宗,学生做题时要善于提炼方法,进行变式训练,以提升自身的核心素养.

(完)