强基计划数学备考系列讲座(2)
——复数与方程

王慧兴

(清华大学附属中学)

强基计划高校校考试题与高考试题突出互补性,本文对这种互补性进行例析.

1 知识技能

复数的知识要点归纳如表1所示.

表1

2 要点解析

1)重要恒等式

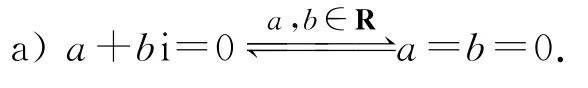
b)共轭与模的活化恒等式:＝|z|2.

c)平行四边形恒等式:|z1＋z2|2＋|z1－z2|2＝2(|z1|2＋|z2|2).

d)拓展:|z1－z2|2＋|z2－z3|2＋|z3－z1|2＋|z1＋z2＋z3|2＝3(|z1|2＋|z2|2＋|z3|2).

e)深化:a3＋b3＋c3－3abc＝(a＋b＋c)(a＋ωb＋ω2c)(a＋ω2b＋ωc)(ω为1的虚立方根).

2)特殊复数(如表2)

表2

3)欧拉公式

最“美”公式eπi＋1＝0(恰好包含数学中五个特殊、关键的数).

4)复数模不等式

a)‖z1|－|z2‖≤|z1＋z2|≤|z1|＋|z2|,右式取“＝”成立的条件是z1＝kz2(k＞0),左式取“＝”的条件是z1＝－kz2(k＞0).

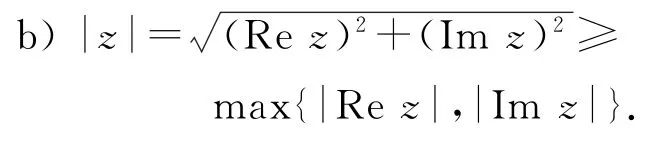
5)旋转计算

在平面上把点B(z1)绕点A(z0)逆时针旋转一个角度θ,得点C(z2),对应复数等式为

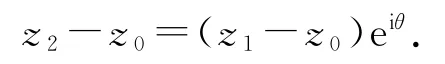
6)复数开方

给定整数n≥2,复数z＝r(cosθ＋isinθ)(r＞0)的n次方根是

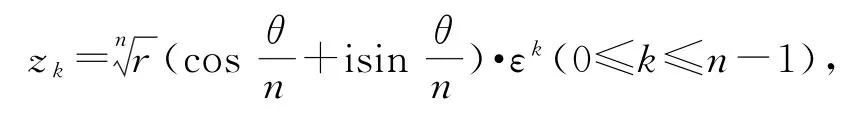
其中ε＝cos是1的一个n次方根,复数z0,z1,…,zn－1在复平面上对应表示的点均匀分布在圆上.

7)单位根及其性质(如表3)

表3

8)复数与方程(如表4)

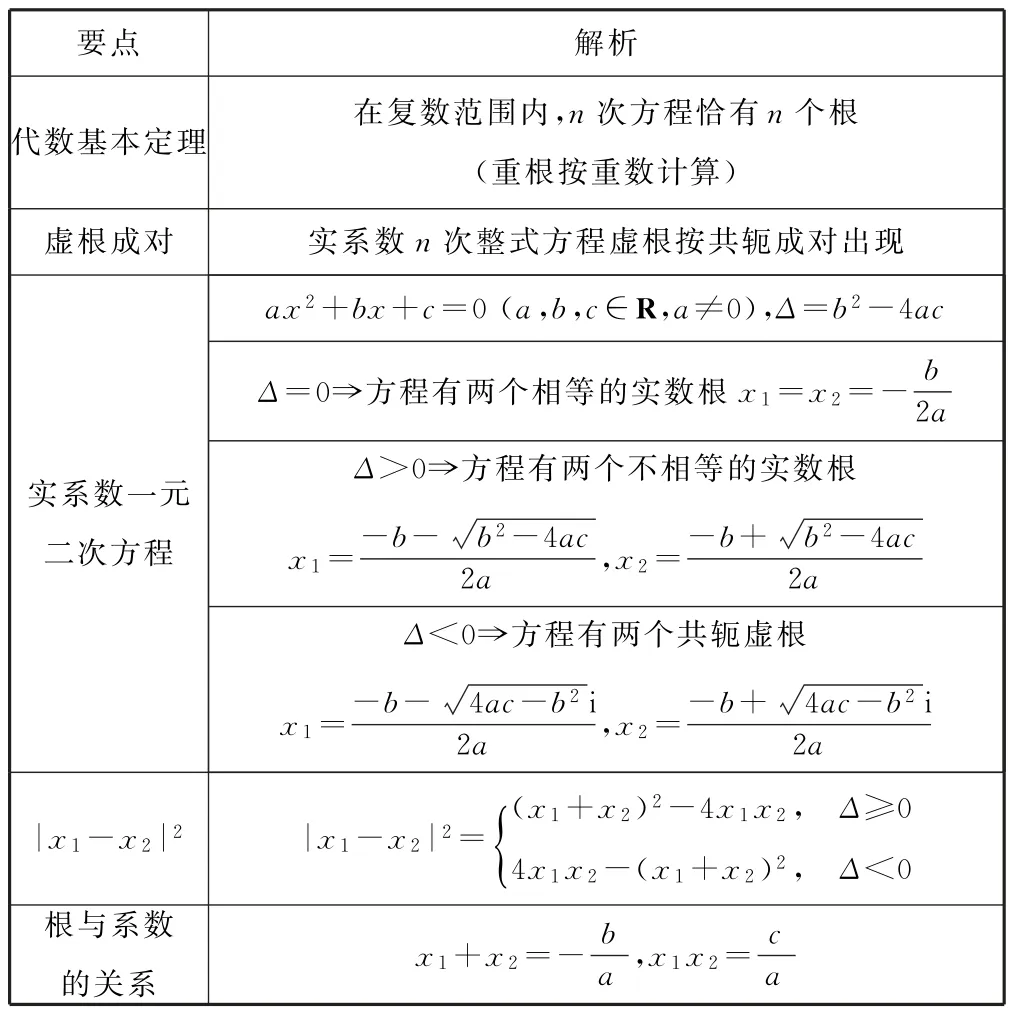
表4

9)复数与三角

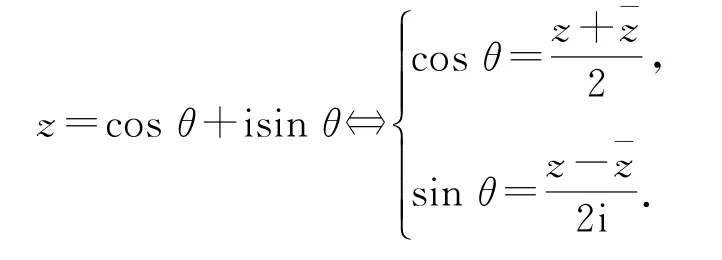
10)复数与多项式

a)多项式插值公式:任给两组复数u0,u1,u2,…,un以及v0,v1,v2,…,vn,则存在至多n次多项式P(z)满足:P(uj)＝vj(j＝0,1,2,…,n),即

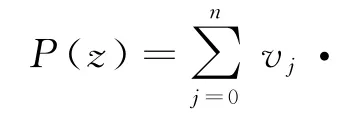
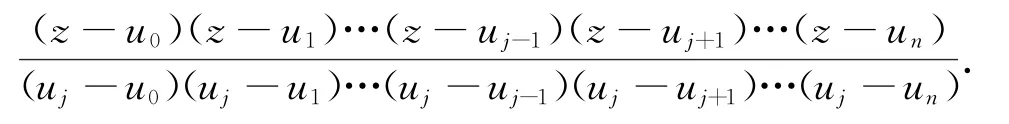
b)因式定理:多项式f(x)被x－a除得的余式是f(a),则(x－a)|f(x)⇔f(a)＝0.

c)整系数整式方程有理根包围圈:整系数整式方程a0xn＋a1xn－1＋…＋an－1x＋an＝0(aj∈Z,0≤j≤n,a0≠0)的有理根x＝r∈u|an,v|a0,u∈N*,v∈Z,(u,v)＝1}.

d)R[x]中不可约多项式只有一次多项式与二次不可约多项式x2＋ax＋b(a2－4b＜0).

e)已知f(x)∈R[x],则f(x)≥0(x∈R)⇔存在g(x),h(x)∈R[x],使得f(x)＝(g(x))2＋(h(x))2.

11)复数与几何(如表5)

表5

12)等幂和算法

给定a1,a2,…,ak－1,ak,记

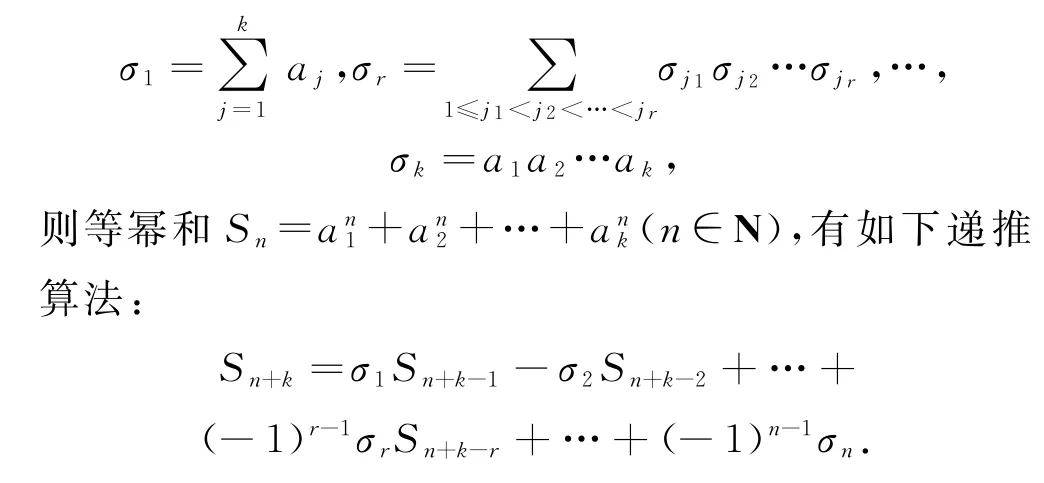
3 典例精析

3.1 复数基本运算

例1求复数z＝并求最小正整数n,使得

3.2 复数与三角

复数与三角、反三角关联的途径主要是复数的三角形式、指数形式以及乘除、乘方与开方运算,n次单位根是建立三角恒等式的一个视角.

例2(清华大学)求复数z＝2＋2e0.4πi＋e1.2πi的模.

3.3 不等式与最值

复数与不等式、最值的关联主要是模与辅角.

例5已知复数z满足|z|＝1,求f＝|z3－3z＋2|的最大值.

按题意,z＝x＋yi(x,y∈R),则x2＋y2＝1,所以

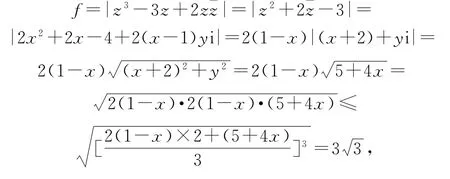
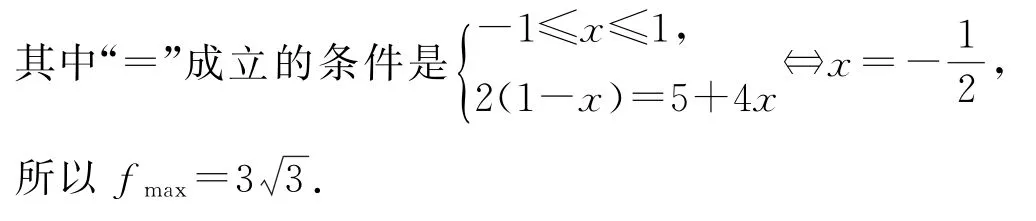
例6已知复数a,b,c,满足|a|2＋|b|2＋|c|2＝1,求证:|a3＋b3＋c3－3abc|≤1.

3.4 复数与方程

复数与方程相互交融,关联广泛.

证明目标等价于2cosθ∈{－2,－1,0,1,2},所以只需证明2cosθ是某个整系数方程的有理根,为此,先证引理.

引理任取n∈N*,存在首一n次多项式p(x)∈Z[x],使得2cosnθ＝p(2cosθ).

引理证明当n＝1 时,取首一1 次多项式p(x)＝x,满足2cosθ＝p(2cosθ);当n＝2时,取首一2次多项式p(x)＝x2－2,得

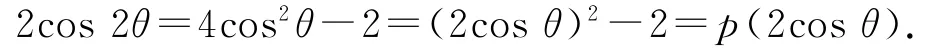
假设对n＜k＋2(k∈N*)都已存在首一n次多项式pn(x)∈Z[x],满足2cosnθ＝pn(2cosθ),由

取首一k＋2次多项式pk＋2(x)＝xpk＋1(x)－pk(x)∈Z[x],得

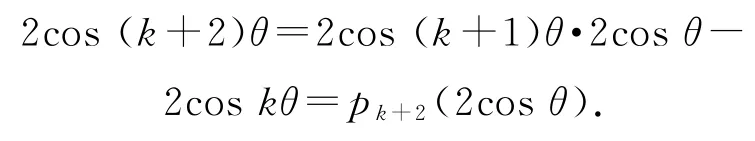
综上,由数学归纳法,引理得证.

由已知,2cosθ∈Q,再由引理,存在首一整系数多项式p(x),使得x＝2cosθ是一个整系数整式方程p(x)＝0的有理根,故2cosθ∈[－2,2]∩Z＝{－2,－1,0,1,2},即cosθ∈{－1,－

3.5 复数与几何

通过复数运算探究几何问题是几何分析的重要方法.

例9(北京大学)单位圆内接五边形的所有边长与对角线的平方和的最大值是( ).

A.15 B.20 C.25 D.以上答案都不对

用复数计算.设内接于单位圆的五边形P1P2P3P4P5各顶点对应复数Pk(zk),则|zk|＝1(k＝1,2,3,4,5),所以

例11在△ABC中,∠ACB＝30°,点M,I分别是△ABC的外心和内心,在边AC和BC上分别取点D,E,使 得AD＝BE＝AB,求证:MI⊥DE,且MI＝DE.

证明如图1所示,以图形所在平面为复平面,其中内心I为原点,同时以P表示点P对应的复数,则D＝,所以

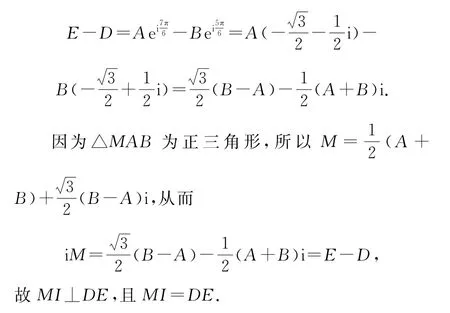
图1

3.6 多项式问题

例12设a,b,c为互异实数,P(x)∈R[x],已知P(x)除以x－a余式为a,P(x)除以x－b余式为b,P(x)除以x－c余式为c,求P(x)除以(x－a)·(x－b)(x－c)的余式.

方法1记P(x)＝(x－a)(x－b)·(x－c)u(x)＋r(x),其中r(x)∈R[x]是至多二次的多项式,所以按题意,r(a)＝P(a)＝a,r(b)＝P(b)＝b,f(c)＝P(c)＝c,所以r(x)＝x.

方法2由插值公式,得

故得恒等式

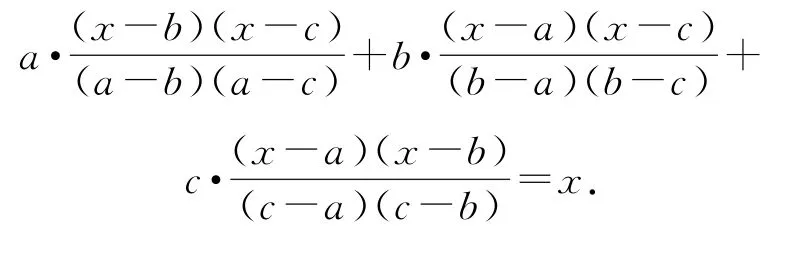
例13给定不同整数m1,m2,…,mn,求证:存在一个整系数n次多项式f(x)同时满足以下两个条件:

(1)f(mi)＝－1(1≤i≤n);

(2)f(x)不能分解为两个次数都不小于1的整系数多项式之积.

证明一方面,n次整系数多项式f(x)＝(xm1)(x－m2)…(x－mn)－1,满足条件(1).

另一方面,下用反证法证f(x)满足条件(2).假设f(x)不满足条件(2),则存在两个次数都不小于1的整系数多项式g(x),h(x),使得f(x)＝g(x)·h(x),因为f(mi)＝－1(i＝1,2,…,n),所以g(mi)·h(mi)＝－1(i＝1,2,…,n),从而g(mi)＋h(mi)＝0(i＝1,2,…,n),但多项式g(x)＋h(x)的次数小于n,所以g(x)＋h(x)＝0,从而f(x)＝－(g(x))2,这与f(x)是首一多项式矛盾.

综上,f(x)＝(x－m1)(x－m2)…(x－mn)－1是满足题设的整系数多项式.

例14(清华大学)以和为两根的有理系数多项式次数最小值是_________.

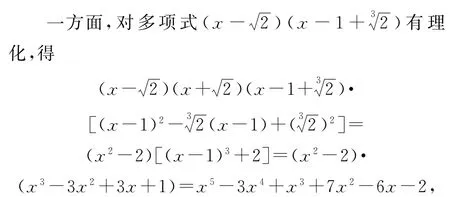
所以m(x)的次数d≤5.

另一方面,下证m(x)的次数d≥5.

假设存在一个次数不超过4的有理系数多项式m(x)＝ax4＋bx3＋cx2＋dx＋e(系数是不全为零的有理数),满足

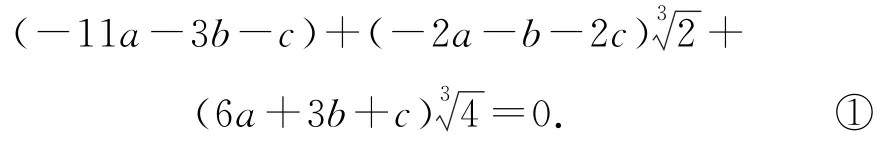
等式①中的有理数a,b,c可视为整数,先证一个引理.

引理a＋＝0(a,b,c∈Q)⇒a＝b＝c＝0.

引理的证明分以下两种情形.

情形一,c＝0,得

从而a＝b＝c＝d＝e＝0,矛盾,故m(x)的次≥5.

综上,m(x)的次数等于5.

下面证明最小的正整数n≥5,为此我们用反证法证明满足条件的n≥5.

当n＝4 时,假设存在有理数ai,bi(i＝1,2,…,n)满足x2＋x＋4＝,则

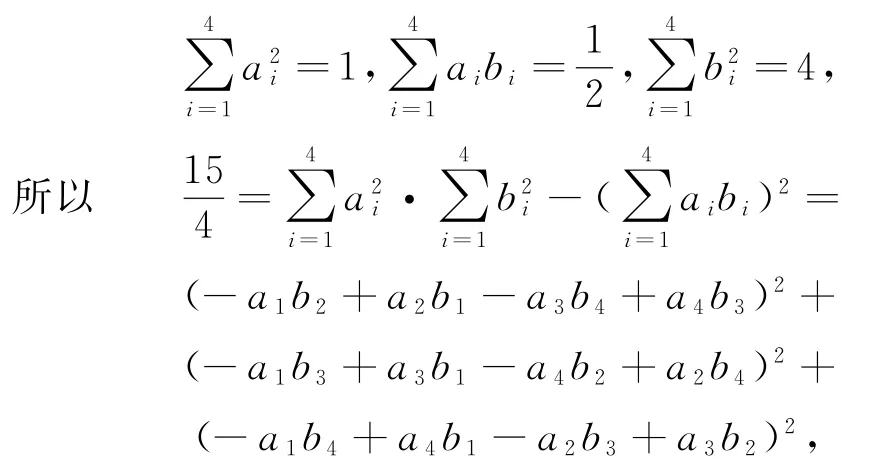
存在整数a,b,c,d满足a2＋b2＋c2＝15d2,模8得

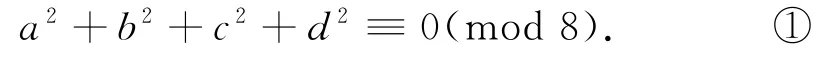
不妨设a,b,c,d中有k(1≤k≤4)个奇数,注意到“奇数的平方模8余1,偶数的平方模8余0或4”.若k＝4,则①即4≡0(mod8),矛盾! 若k＝3,则3＋(2p)2≡0(mod8),导致3≡0(mod4),亦矛盾! 若k＝2,则2＋(2p)2＋(2q)2≡0(mod8),导致2≡0(mod4),亦矛盾! 若k＝1,则1＋(2p)2＋(2q)2＋(2r)2≡0(mod8),导致1≡0(mod4),亦矛盾!

综上,n≠4,从而n≥5,故所求最小正整数n＝5.

4 实战演练

1.下面两个命题:甲,设a,b,c∈C,如果a2＋b2＞c2,则a2＋b2－c2＞0.乙:设a,b,c∈C,如果a2＋b2－c2＞0,则a2＋b2＞c2.则这两个命题的正误是_________.

4.已知复数z满足|z|＝1,求f＝|z2－z－2|的最大值与最小值,并给出对应的复数z.

5.关于x的方程x2－(2i－1)x＋(3m－i)＝0(m∈R)有实根,求m的值,并解方程.

6.已知整系数四次方程x4＋px3＋qx2＋rx＋s＝0的四个根在复平面内对应的点恰好是一个正方形的四个顶点,求这个正方形面积的最小值.

7.已知z∈C满足11z10＋10iz9＋10iz－11＝0,求证:|z|＝1.

8.求一个以x＝为唯一实数根的三次整系数多项式p(x).

9.方程z10＋(13z－1)10＝0有10个虚根,记为zj(j＝1,2,3,4,5),求f＝的值.

10.模为1的复数z1,z2,z3满足z1＋z2＋z3≠0,求.

11.求最小实数λ,使得对满足z1＋z2＋z3＝0以及|zj|＜1(j＝1,2,3)的复数z1,z2,z3,都有

12.设整数k不能被5整除,求证:多项式x5－x＋k不能分解为两个次数较低的整系数多项式;如果k是5的倍数,有什么结果?

13.给定凸四边形ABCD(如图2),若在四边形ABCD内有个点M,使得△AMB和△CMD均为等腰三角形(AM＝MB,CM＝MD),并且∠AMB＝∠CMD＝120°.试证:存在一个点N,使得△BNC和△DNA都是正三角形.

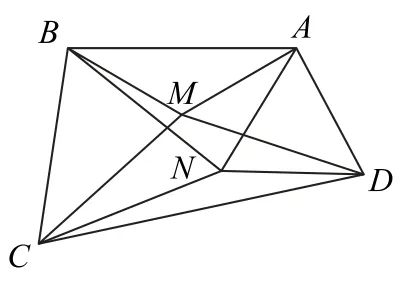
图2

14.给定一个正整数n,设n个实数a1,a2,…,an满足下列n个方程:

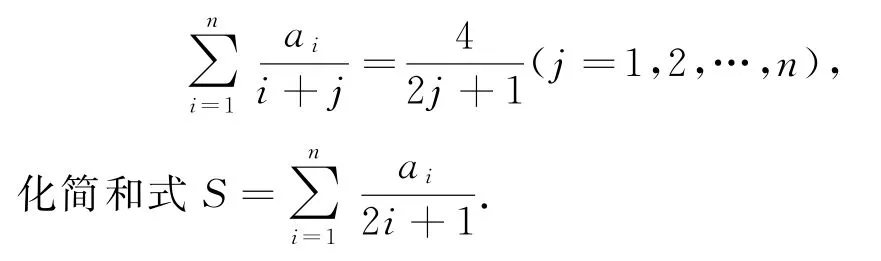
15.设n次多项式f(x)满足f(k)＝(k＝0,1,2,…,n),求f(n＋1).

16.已知复系数n次多项式f(z)＝c0zn＋c1zn－1＋…＋cn－1z＋cn(c0≠0),求证:必存在一个复数z0满足|z0|≤1,使得|f(z0)|≥|c0|＋|cn|.

(完)