巧用换元法 妙证不等式

王 宠 陈 超

(中国人民大学附属中学丰台学校)

在证明不等式的过程中,将不等式中的变量进行适当代换,使不等式得以证明,这种方法称为不等式证明中的换元法.不等式证明中的换元法是换元思想的重要体现.

换元法没有固定模式,常用的方法是三角换元法和代数换元法,其中三角换元法有一定的规律性.若问题中含有“x2＋y2＝r2,x2＋y2≤r2,”,可以考虑用“sinα,cosα”进行代换,尤其是r＝1时,这样代换的优势更为明显,进行这些代换的理论依据是sin2α＋cos2α＝1以及圆x2＋y2＝r2的参数方程为y＝rsinα,x＝rcosα;若问题中含有“|x|≤a”,可以考虑设“x＝asinα”或“x＝acosα”,其理论依据是|sinα|≤1,|cosα|≤1;类似地,对于“和“”可分别进行“x＝rtanα”和“x＝rsecα”代换.需要特别指出的是,当时,tanα可取全体实数,所以tanα可以代换任意实数.

对于代数换元法,虽然它的规律性不像三角换元法那么强,但是也有一些可以遵循的规律.如果题目中出现类似“已知a＞b＞c＞0”的条件,这时可以令x＝a－b,y＝b－c,z＝c,从而将原来关于a,b,c的式子转化为关于x,y,z的式子,并且此时x,y,z只需为正实数即可.如果题目中出现类似“a,b,c是三角形的三边”的条件,此时可以令x＝,从而得到a＝y＋z,b＝x＋z,c＝x＋y,并且此时x,y,z只需为正实数即可.

尽管换元法没有固定的模式,但有一个原则是必须遵守的,那就是进行变量代换时,新变量的变化范围必须确保原来变量的变化范围不发生变化,这是换元法的重点,也是难点.下面结合一些具体的题目,谈一谈换元法在不等式证明中的应用.

例1求证:函数f(x)＝在x∈[0,1]上的最小值是1,最大值是

分析看到x和,注意到二者的平方和等于1,所以可以进行三角换元,令x＝cosα.因为题中要求x∈[0,1],所以α∈[0,],从而sinα,那么接下来就需要利用三角函数的相关知识来处理问题了.

证明令x＝cosα,α∈那么sinα,从而

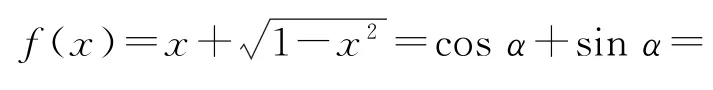
例2已知x2＋y2≤1,求证:

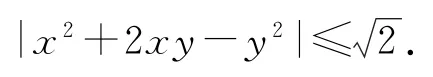
分析x2＋y2≤1可理解为它所确定的平面区域为圆形区域{(x,y)|x2＋y2≤1},这样的x和y可以表示为x＝rcosα,y＝rsinα,其中r∈[0,1],α∈[0,2π).

证明令x＝rcosα,y＝rsinα,其中r∈[0,1],α∈[0,2π).于是

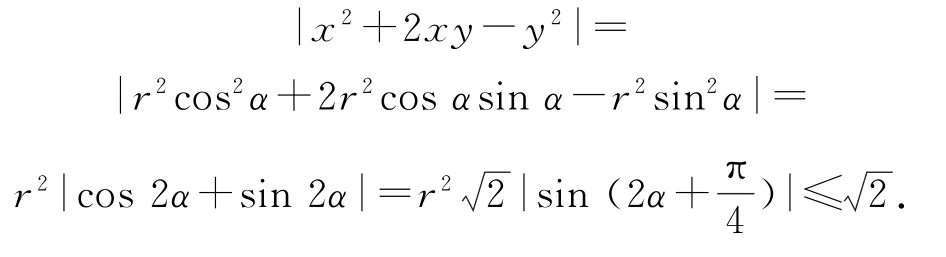
例3已知0＜x＜1,求证:

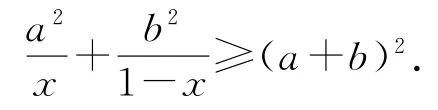
分析注意到当0＜x＜1时,0＜1－x＜1,并且x＋(1－x)＝1.联想到sin2α＋cos2α＝1,作变换x＝cos2α或sin2α,简化运算.

证明考虑到0＜x＜1,令x＝sin2α,α∈(0,,则1－x＝cos2α,从而

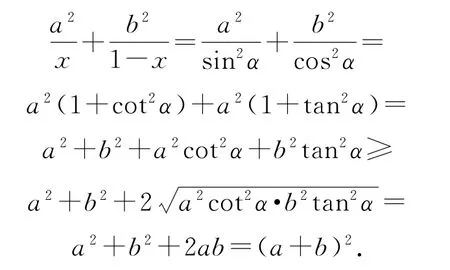
例4已知|x|≤2,求证:|3x－x3|≤2.

分析由|x|≤2,可知||≤1,因此可以考虑对作“sinα,cosα”代换.

证明考虑到|x|≤2,令x＝2sinα,α∈[0,2π).从而

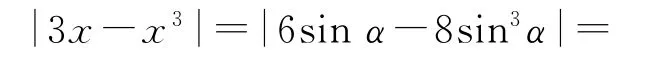
2|3sinα－4sin3α|＝2|sin3α|≤2.

例5已知a＞b＞c,求证:

分析因为a－c＝(a－b)＋(b－c),并且a＞b＞c,这时可以考虑设x＝a－b,y＝b－c,此时x和y均为正实数.

证明因为a＞b＞c,所以a－b＞0,b－c＞0,a－c＞0.令x＝a－b,y＝b－c,则x＞0,y＞0,并且a－c＝x＋y.从而原不等式转化为即(x＋y≥4,亦即≥4.

而上述不等式成立是显然的,并且当且仅当x＝y,即2b＝a＋c时取等号.

综上,原不等式成立.

补充本题所证结论可推广为一般情形:若n∈N,n≥2,a0＞a1＞a2＞…＞an,则

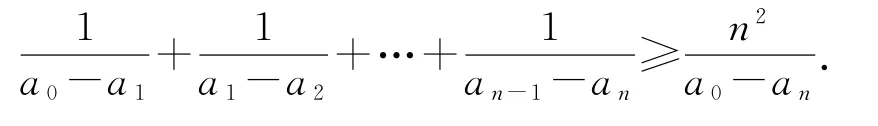
例6已知a,b,c是三角形的三边长,求证:

而上述不等式成立是显然的,并且当且仅当x＝y＝z,即a＝b＝c时取等号.

综上,原不等式成立.

例7已知a,b,c为正实数,并且满足a2＋b2＋c2＝1,求证:

分析注意到待证不等式形式较为复杂,考虑通过代数换元简化其形式.

证明令.因为a,b,c为正实数,所以x＞0,y＞0,z＞0,并且a2＝xz,b2＝xy,c2＝yz,因此xz＋xy＋yz＝1.从而原不等式转化为x＋y＋z≥,而上述不等式成立是显然的.事实上,有

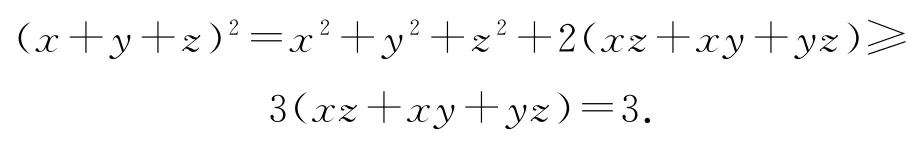
综上,原不等式成立.

例8已知a,b,c为正实数,求证:的最小值为

分析对于分式,通过换元可以使分母的形式变得简单,这样处理起来会方便很多.

证明令x＝a＋2b＋c,y＝a＋b＋2c,z＝a＋b＋3c.因为a,b,c为正实数,所以x＞0,y＞0,z＞0,并且a＝5y－x－3z,b＝x＋z－2y,c＝z－y.从而

综上,命题得证.

例9求证:

分析由于a∈R,所以可以考虑利用公式1＋tan2α＝sec2α换元.式中里面的“4”提示我们可以令a＝2tanα.当然,本题也可以用代数换元法来证明.

由函数的相关知识可知函数f(t)＝t＋在[2,＋∞)上单调递增,所以当t＝2时,f(t)有最小值为.因此原不等式成立.

通过以上几道例题,相信大家对利用换元法证明不等式有了一个较为笼统的认识.在利用换元法证明不等式的过程中,我们要善于观察,通过引入新的变量,对题目进行转化,使隐含的条件显露出来,将已知和结论关联起来,以便迅速找到解题思路.不等式的证明方法繁多,只有不断总结和思考,才能融会贯通.

链接练习

链接练习参考答案

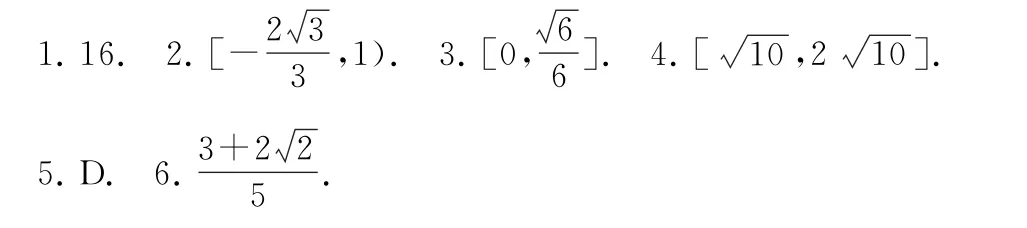
(完)