反证法及其应用

彭长军

(甘肃省嘉峪关市第二中学)

1 概念剖析

1.1 定义

反证法是从要证明结论的否定出发,以有关的定义、公理、定理为依据,结合命题的条件进行推理,直到推出矛盾,从而断定命题结论的否定不能成立,也就断定了命题成立.

1.2 反证法的基本思想

反证法的基本思想是否定结论就会导致矛盾,它可以用下面的程序来表示:

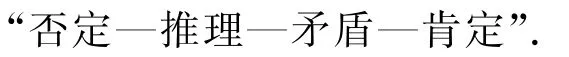
“否定”——假设所要证明的结论不成立,而结论的反面成立.

“推理”——从已知条件和假设出发,引用一系列的论据进行推理.

“矛盾”——通过推导,推出与实际不符,与公理、定理、定义、题设等矛盾.

“肯定”——由于推理过程正确,故矛盾是由假设所引起的,因此假设是错误的,从而肯定原结论是正确的.

1.3 反证法的步骤

否定结论—推出矛盾—否定假设—肯定结论,其中推出矛盾是关键.

1.4 应用反证法的原则

正难则反,即如果一个命题的结论难以直接证明可考虑用反证法.

1.5 宜用反证法证明的命题

适合用反证法的常见题型:1)易导出与已知矛盾的命题;2)一些基本定理;3)“否定性”命题;4)“唯一性”命题;5)“必然性”命题;6)“至少”“至多”型命题.

1.6 需要注意的两点

1)反证法与分析法的区别.

分析法是从命题的结论出发,寻求使结论成立的(充分)条件;而反证法则是从结论的反面出发,推出矛盾.

2)应用反证法证明命题时,反设必须恰当,如“都是”的否定是“不都是”,“至少一个”的否定是“不存在”等.

在这里,我们也要把反证法和证明命题的“逆否命题”为真命题区分开来,两者都是从“否定”结论开始,但证明命题的“逆否命题”为真命题时是从结论的否定出发,经过推理,推出条件的否定,如证明命题“若x2＋y2＝0,则x＝y＝0”时,可以证明它的逆否命题“若x,y中至少有一个不为0,则x2＋y2≠0”.此时,显然要从结论的否定出发,即若x,y中至少有一个不为0,不妨设x≠0,则x2＞0,所以x2＋y2＞0,即x2＋y2≠0.于是命题得证.

2 典例剖析

2.1 结论是肯定型命题的证明

例1若a,b是自然数,且a与b的积是奇数,用反证法证明a与b都是奇数.

证明假设a,b不都是奇数,则a,b中必存在着偶数,不妨设a为偶数,则ab必为偶数,这与题设ab为奇数相矛盾,故a与b都是奇数.

【跟踪训练】若p∈Z,且p2是偶数,求证:p也是偶数.

证明假设p是奇数,则p＝2k－1(k∈Z),所以p2＝4k2－4k＋1为奇数,这与p2是偶数矛盾,故p是偶数.

例2已知函数f(x)在R 上单调递增,a,b是实数,证明命题“如果f(a)＋f(b)＞f(－a)＋f(－b),那么a＋b＞0”.

证明假设a＋b≤0,即a≤－b,则由f(x)在R上单调递增,知f(a)≤f(－b),同理,f(b)≤f(－a),所以f(a)＋f(b)≤f(－a)＋f(－b),这与已知条件f(a)＋f(b)＞f(－a)＋f(－b)矛盾,故原命题成立.

例3已知p＞0,q＞0,且p3＋q3＝2,求证:p＋q≤2.

证明假设p＋q＞2,则p＞2－q,p3＞(2－q)3＝8－12q＋6q2－q3,所以p3＋q3＞6q2－12q＋8,即2＞6q2－12q＋8,q2－2q＋1＜0,亦即(q－1)2＜0,这与(q－1)2≥0矛盾,故p＋q≤2.

【跟踪训练】若a＞0,b＞0,a3＋b3＝2.求证:a＋b≤2,且ab≤1.

证明假设a＋b＞2,则a3＋b3＝(a＋b)(a2－ab＋b2)＝(a＋b)[(a＋b)2－3ab]＞2(22－3ab),即2＞2(4－3ab),所以

另一方面,2＝a3＋b3＝(a＋b)(a2＋b2－ab)≥(a＋b)(2ab－ab)＝(a＋b)·ab＞2ab,所以

显然,①与②矛盾,故a＋b≤2.

假设ab＞1,则

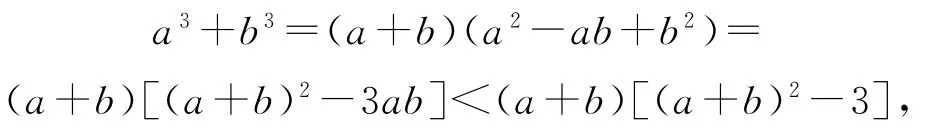
因为a3＋b3＝2,所以(a＋b)3－3(a＋b)－2＞0,即

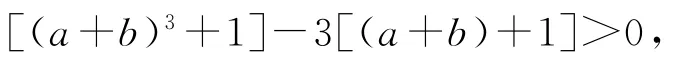
所以(a＋b＋1)[(a＋b)2－(a＋b)＋1]－3(a＋b＋1)＞0,所以(a＋b＋1)[(a＋b)2－(a＋b)－2]＞0,从而(a＋b＋1)2(a＋b－2)＞0,a＋b＞2,这与a＋b≤2矛盾,所以假设不成立,故ab≤1成立.

综上,a＋b≤2,且ab≤1.

例4已知定义在实数集R 上的函数f(x),对任意x,y都有f(x＋y)＋f(x－y)＝2f(x)f(y)成立,且方程f(x)＝0存在最小正根c.求证:

(1)f(0)＝1,且f(x)是偶函数;

(2)|f(x)|≤1.

证明(1)令x＝y＝0,得f(0)＝[f(0)]2,所以f(0)＝0 或1.若f(0)＝0,则∀x＞0,y＝0,有2f(x)＝0,即f(x)＝0,则f(x)无最小正根,则0为方程f(x)＝0的根,这与方程f(x)＝0存在最小正根c矛盾,所以f(0)≠0,故f(0)＝1.又令x＝0,得

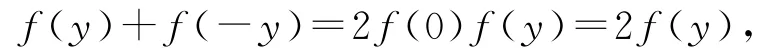
即f(－y)＝f(y),所以f(x)是偶函数.

(2)当x＝y时,f(2x)＋f(0)＝2f2(x),即f(2x)＝2f2(x)－f(0)＝2f2(x)－1,又f(c)＝0,于是,假设存在实数x0使得|f(x0)|＞1,则逆用对应法则,有

又由f(c＋x0)＋f(c－x0)＝2f(c)f(x0)＝0,得f(c＋x0)＝－f(c－x0),所以

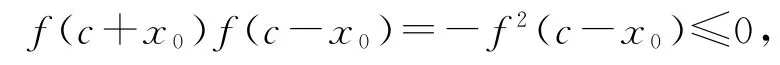
这与上式矛盾.故对任意x∈R,都有|f(x)|≤1.

2.2 结论是否定型命题的证明

A.有3个 B.有0个

C.至少一个 D.至多一个

例7已知a,b,c都是小于1 的正数,求证:(1－a)b,(1－b)c,(1－c)a不能都大于

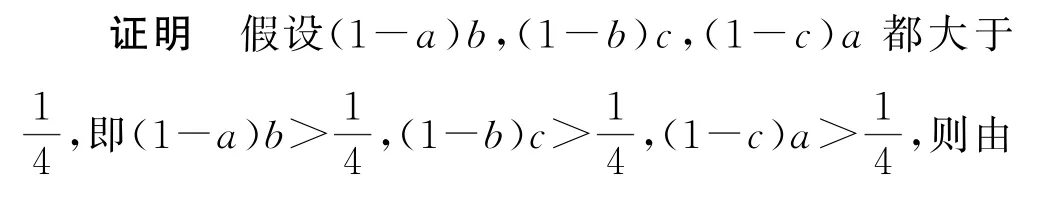
由a,b,c成等差数列,得

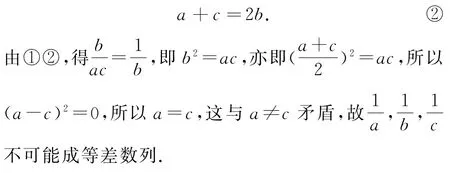
例9等差数列{an}的前n项和为Sn,a1＝1＋S3＝9＋

(1)求数列{an}的通项an与前n项和Sn;

(2)设bn＝,求证:数列{bn}中任意不同的三项都不可能成为等比数列.

例10直线y＝kx＋m(m≠0)与椭圆Wy2＝1相交于A,C两点,O是坐标原点.

(1)当点B的坐标为(0,1),且四边形OABC为菱形时,求AC的长;

(2)当点B在W上且不是W的顶点时,证明:四边形OABC不可能为菱形.

(1)因为四边形OABC为菱形,所以AC与OB互相垂直且平分.于是可设A(t,),代入椭圆方程,得＝1,即t＝,所以

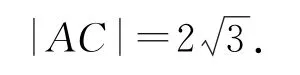
(2)假设四边形OABC为菱形,则AC⊥CB,因为点B不是W的顶点,所以k≠0.由

消y并整理,得(1＋4k2)x2＋8kmx＋4m2－4＝0.

2.3 结论中含有“至少”或“至多”型命题的证明

例11已知函数f(x)对其定义域内的任意两个实数a,b,当a＜b时,都有f(a)＜f(b),证明:函数f(x)至多有一个零点.

证明假设函数f(x)有两个不同的零点x1,x2,且x1＜x2,则由零点的定义,知f(x1)＝0,f(x2)＝0,所以

又由题设条件知,当x1＜x2时,有f(x1)＜f(x2),这与式①矛盾,因此假设不成立,故函数f(x)至多有一个零点.

例12设有实系数二次方程ax2＋2bx＋1＝0与cx2＋2dx＋1＝0,若a,bd,c成等差数列,求证:上述两个方程中至少有一个方程有实根.

证明假设两个方程都无实根,则

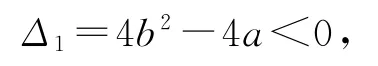
且Δ2＝4d2－4c＜0,即a＞b2,且c＞d2,则

由a,bd,c成等差数列,得a＋c＝2bd,这与式①矛盾,因此假设不成立,故原命题得证.

例13若实数b1,b2,c1,c2满足b1b2＝2(c1＋c2),求证:实系数一元二次方程x2＋b1x＋c1＝0和x2＋b2x＋c2＝0中至少有一个方程有实数根.

【跟踪训练】(1)设实系数二次方程ax2＋bx＋c＝0与dx2＋ex＋f＝0,且ac,be,df成等比数列,求证:上述两个方程中至少有一个方程有实根.

(2)已知a≥－1,求证x2＋4ax－4a＋3＝0,x2＋(a－1)x＋a2＝0,x2＋2ax－2a＝0这三个方程中至少有一个方程有实数根.

例14设f(x)＝2x2＋ax＋b,求证:|f(1)|,|f(2)|,|f(3)|中至少有一个不小于1.

证明因为f(1)＝a＋b＋2,f(2)＝2a＋b＋8,f(3)＝3a＋b＋18,设

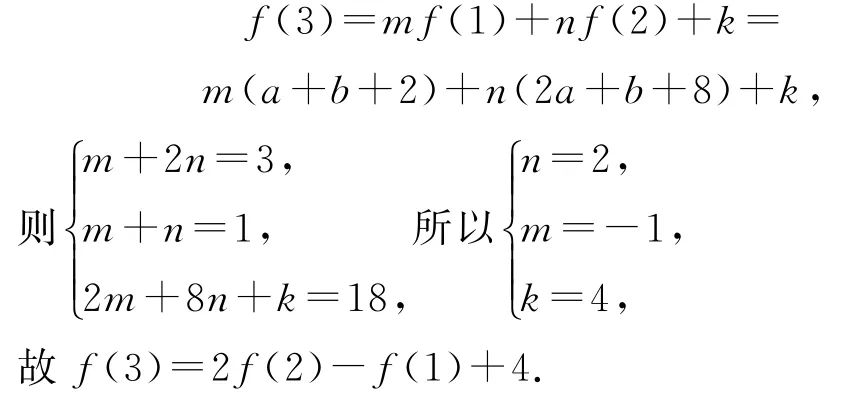
假设|f(1)|,|f(2)|,|f(3)|都小于1,则

由f(3)＝2f(2)－f(1)＋4,得f(1)－2f(2)＋f(3)＝4,而|f(1)|＋2|f(2)|＋|f(3)|≥|f(1)－2f(2)＋f(3)|＝4,这与①矛盾,所以假设不成立,故原不等式成立.

注本例也可这样得到矛盾:假设|f(1)|,|f(2)|,|f(3)|都小于1,则f(1),f(2)∈(－1,1),所以f(3)＝2f(2)－f(1)＋4∈(1,7),这与假设|f(3)|＜1矛盾,所以假设不成立,故原不等式成立.

2.4 结论是判断或确定型命题的证明

例16(2021年浙江卷8)已知α,β,γ是互不相同的锐角,则在sinαcosβ,sinβcosγ,sinγcosα三个值中,大于的个数的最大值是( ).

A.0 B.1 C.2 D.3

例17如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,试判断△A2B2C2的形状.

由条件知,△A1B1C1的三个内角的余弦值均大于0,所以△A1B1C1是锐角三角形.

假设△A2B2C2是锐角三角形,则由

3 小结

反证法是从结论的反面出发,即假设命题不成立(在原命题的条件下,结论不成立),经过一系列正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立.

当一个命题用直接法不易证明时,可考虑用反证法,尤其是结论中出现“至多”“至少”“唯一”或结论是否定形式的命题,最适宜用反证法证明.

用反证法证明命题的关键是:在正确的推理下得出矛盾,矛盾可以是与已知条件矛盾,与假设矛盾,与定义、公理、定理矛盾,与自身矛盾,与事实矛盾等,但推导出的矛盾必须是明显的.

用反证法证明命题时,第一步否定结论必须恰当,这是证明命题的出发点,在这个基础上,经过推理推出矛盾是关键.否定结论的实质就是假设结论的反面成立,为了能更好地否定结论,我们必须要熟记一些常见的否定表示(如表1).

表1

(完)