立足数学核心素养 分析中考压轴题



【摘 要】 本文用核心素养的三个水平分析压轴题,建议数学试题命制中可融入核心素养制作多维细目表,用核心素养三个水平来调控试题的难度,也可评定结构不良试题的得分.启发教师在教学中应培养学生数学正迁移能力,精准把握学情,来逐层落实数学核心素养.
【关键词】 核心素养;三个水平;正迁移;逐层
《普通高中数学课程标准(2017年版)》提出发展学生的六个数学核心素养,切实提升思维品质和关键能力.中考数学最后一题,又称为压轴题,有区分选拔功能.笔者立足这六个数学核心素养来分析2018—2020这三年的陕西省数学中考最后一题(第25题),揭示命题特点,给出命题建议和教学建议.
1 相关概念知识
喻平教授[1]分析了布鲁姆评价模型、PISA数学素养评价框架、SOLO分类评价理论,提出将数学核心素养划分为三个水平,从低到高依次是知识理解、知识迁移和知识创新.同时,参考李先东老师和吴增生老师[2]對初中数学核心素养的三个水平的划分标准,对各试题进行素养观察.数学抽象A、逻辑推理R、数学建模M、数学运算C、直观想象I、数据分析D,A1,A2,A3分别对应数学抽象的三个水平,其他素养类似.
2 对近三年陕西省数学中考第25题评析
2.1 2018年第25题试题呈现及分析
问题提出
(1)如图1,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为;(2分)
问题探究
(2)如图2,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值;(3分)
问题解决
(3)如图3,AB,AC,BC是某新区的三条规划路,其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB,AC路边分别建物资分站点E,F.也就是,分别在BC、线段AB和AC上选取点P,E,F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE,EF和FP.为了快捷环保和节约成本要使得线段PE,EF,FP之和最短,试求PE+EF+FP的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)(7分)
核心素养水平分析:
(1)如图4,能画出外接圆,则达到直观想象素养水平1的要求;三步演绎推理出结果,标定为逻辑推理素养水平1.分值标定为I1-1,R1-1.
(2)如图5,能发现当射线MO与⊙O相交时,PM最大,则达到直观想象素养水平2的要求;能严谨地论证为什么此时MN最大,则达到逻辑推理素养水平2的要求.分值标定为I2-2,R2-1.
(3)如图6,若能在陌生情境中跨学科联想到物理中的“光行最短”原理,将边AB和AC看作平面镜,点光源P发出的光线经过两次反射回到点P,进而在BC上找一点P,构造将军饮马模型,且发现当连接AO时AP最小,如图7,此时线段MN最小,则达到直观想象素养水平3和数学建模素养水平3的要求,其中也考查了数学抽象素养水平3;能严谨地证明为什么线段MN是PE+EF+PF的最小值,和证明为什么当连接AO时AP最小,则达到逻辑推理素养水平3的要求;能在较复杂的情境中选择合适的运算方法,并体会代数推理,则达到数学运算素养水平3的要求.分值标定为I3-2,A3-1,R3-1,M3-1,C3-2.
2.2 2019年第25题试题呈现及分析
问题提出
(1)如图8,已知△ABC,试确定一点D,使得以A,B,C,D为顶点的四边形为平行四边形,请画出这个平行四边形;(2分)
问题探究
(2)如图9,在矩形ABCD中,AB=4,BC=10,若要在该矩形中作出一个面积最大的△BPC,且使∠BPC=90°,求满足条件的点P到点A的距离;(5分)
问题解决
(3)如图10,有一座草根塔A,按规定,要以塔A为对称中心,建一个面积尽可能大的形状为平行四边形的草根景区BCDE.根据实际情况,要求顶点B是定点,点B到塔A的距离为50米,∠CBE=120°,那么,是否可以建一个满足要求的面积最大的平行四边形景区BCDE?若可以,求出满足要求的平行四边形BCDE的最大面积;若不可以,请说明理由.(塔A的占地面积忽略不计)(5分)
核心素养水平分析:
(1)能在熟悉的情境中画出平行四边形,则达到直观想象素养水平1的要求.分值标定I1-2.
(2)如图11,能构造出以边BC为直径的圆,则达到直观想象素养水平2的要求;如果能用准确的数学语言演绎推理出所有满足条件的点P,且论证在OB>AB的条件下,⊙O一定与AD相交于点P,则达到逻辑推理素养水平2的要求.分值标定为I2-3,R2-2.
(3)能由平行四边形的性质推理出∠BE′D=60°,且严谨地论证EF≤E′A,标定为逻辑推理素养水平2;构造出⊙O,如图12,发现当E′为中点时,面积最大,标定为直观想象素养水平3;计算得到结果,则达到数学运算素养水平2的要求.分值标定为R2-1,C2-2,I3-2.
2.3 2020年第25题试题呈现及分析
问题提出
(1)如图13,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是;(3分)
问题探究
(2)如图14,AB是半圆O的直径,AB=8.P是AB上一点,且PB=2PA,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长;(4分)
问题解决
(4)如图15,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).
①求y与x之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.(5分)
核心素养水平分析:
(1)能在熟悉的几何情境中写出证明过程,则达到逻辑推理素养水平1的要求.分值标定R1-3.
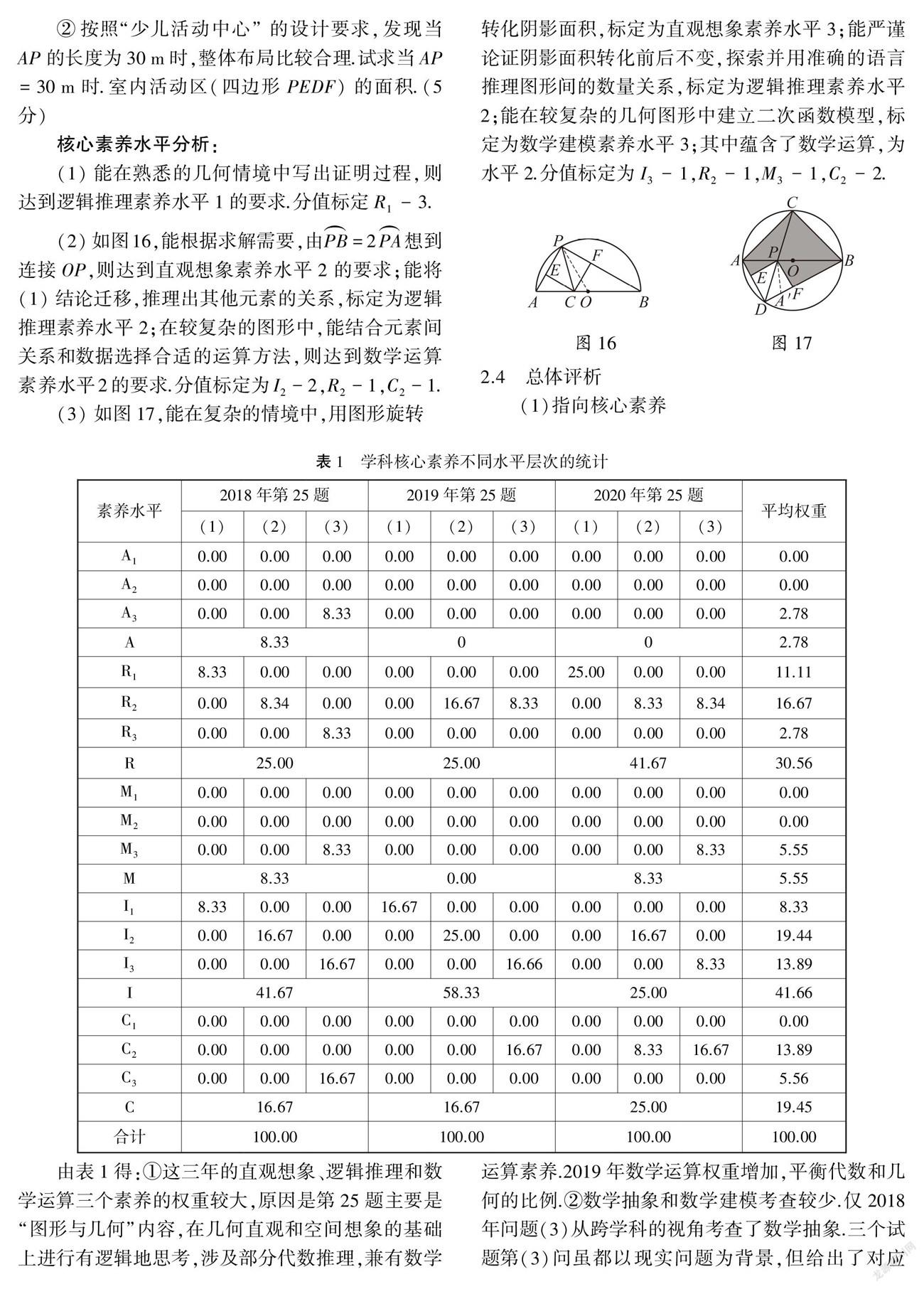
(2)如图16,能根据求解需要,由PB=2PA想到连接OP,则达到直观想象素养水平2的要求;能将(1)结论迁移,推理出其他元素的关系,标定为逻辑推理素养水平2;在较复杂的图形中,能结合元素间关系和数据选择合适的运算方法,则达到数学运算素养水平2的要求.分值标定为I2-2,R2-1,C2-1.
(3)如图17,能在复杂的情境中,用图形旋转转化阴影面积,标定为直观想象素养水平3;能严谨论证阴影面积转化前后不变,探索并用准确的语言推理图形间的数量关系,标定为逻辑推理素养水平2;能在较复杂的几何图形中建立二次函数模型,标定为数学建模素养水平3;其中蕴含了数学运算,为水平2.分值标定为I3-1,R2-1,M3-1,C2-2.
2.4 总体评析
(1)指向核心素养
由表1得:①这三年的直观想象、逻辑推理和数学运算三个素养的权重较大,原因是第25题主要是“图形与几何”内容,在几何直观和空间想象的基础上进行有逻辑地思考,涉及部分代数推理,兼有数学运算素养.2019年数学运算权重增加,平衡代数和几何的比例.
②数学抽象和数学建模考查较少.仅2018年问题(3)从跨学科的视角考查了数学抽象.三个试题第(3)问虽都以现实问题为背景,但给出了对应的几何图形,免去了从实际问题抽象出几何图形的过程,可能由于脱离几何图形来描述现实情境容易产生歧义.2020年问题(3),若题目中不给定变量x和y,直接让求阴影面积的最大值,则要求考生在体会图形的形成过程中,来找到决定阴影面积的关键量是线段AP的长度,自己引入变量来列关系式,这样会考查到数学抽象素养.
(2)关注内在迁移
这三道压轴题的五个核心素养水平2的总权重为50%,考查知识迁移最多.2018年问题(1)中顶角为120°的等腰三角形的线段和角之间的数量关系是解决(3)要用到的.问题(2)中圆内部一点到圆上的距离,什么时候最短或最长:该点和圆心的连线与圆的交点就是最短位置或最长位置,点在圆外也是一样的,这样(2)的活动经验可以来解决(3).2019年问题(1)中根据平行四边形的性质画图,(2)中寻找并求出△BCP面积最大值的数学活动经验,可以迁移解决(3).2020年问题(2)、(3)均用到了(1)的图形和结论,(2)中圆周角定理的推论也是求解(3)要用到的.每个试题的三问之间考查了学生的数学迁移能力.试题的三问从易到难,层层递进,是一个有机的整体.考查考生是否能识别三问之间的共同要素逐步求解问题(3).
在设计各小问时,如果后一问用到前一问的结论,考查较简单;若后一问用到前一问的解题思路和活动经验,相对提升了难度,整个图形的元素关系发生较大改变,相应的核心素养水平要求更高.
3 命题建议
3.1 融入核心素养制作多维细目表
这三个试题主要载体是特殊四边形和三角形內容,蕴含数形结合思想,指向直观想象和逻辑推理;2020年增加了函数,指向数学建模和数学运算.可见,“四基”影响着核心素养的内容(即考查哪个核心素养).由于核心素养的三个水平分别对应知识理解、知识迁移和知识创新三种不同的能力,可以用三个水平来调控试题的难度和区分度.一般地,同一个知识内容,核心素养水平级越高,考查的素养类别越多,试题难度就越大.如2018年的第25题第(3)问是这三个试题中难度最大的,考查了五个素养,且均为水平3.基于以上分析,可以制定表2,保证压轴题的综合性和区分度.
3.2 用“三个水平”评价结构不良试题
可命制结构不良试题[3],如当试题的问题部分的内容缺失或冗余时,让考生通过补充问题或删减多余的问题内容,来提出新问题并解答;或让考生改变题目条件,写出能产生的新结论.对于结构不良试题的评分,可分析所提出的新问题或新结论是对应核心素养的哪个水平,水平越高赋分越高.
4 教学启示
4.1 “逐层”落实数学核心素养
初中数学分为“数与代数”“图形与几何”“概率与统计”和“综合与实践”四个领域,具体地,“数与代数”领域主要指向数学抽象、数学建模、代数推理和数学运算;“图形与几何”内容主要指向直观想象和逻辑推理;“概率与统计”主要指向数据分析.而数学核心素养被划分为知识理解、知识迁移和知识创新三个水平层次,教师应针对每个领域知识,系统地分析教材内容,依托数学内容环环相扣的特点来循序渐进地逐层发展学生的数学核心素养.教师在备课中应分析学生已有的与该章节内容有关的数学核心素养水平级情况,再结合每节教学内容,进一步思考应设置怎样的学习驱动任务,让学生达到相应的核心素养的哪个层级,最终提高数学核心素养水平.4.2 培养数学正迁移能力[4]
一方面,当学习A和学习B有共同要素时,迁移就能发生.学习者能否识别概括出共同要素很关键,故可通过提高学习者的概括能力来培养数学正迁移能力.另一方面,当学习者大脑中有一个稳定清晰的数学认知结构时,面对新任务,就能唤醒已有的数学知识和经验来解决问题.如2018年第25题,对于最短路径,初中阶段数学相关依据是“两点之间,线段最短”和“垂线段最短”,物理中有“光行最短”原理,在“将军饮马”模型的构造中关联着等腰三角形的性质.考生若能将以上知识及其关系清晰地有逻辑性地存储在大脑中,形成自己的认知结构,题目便能求解.教师应挖掘知识间的内在逻辑关系,把知识点放在知识结构中去认识,基于单元整体乃至整个初中学段的课程的角度设计教学案例,来完善学生的认知结构.
参考文献
[1]喻平.学科关键能力的生成与评价[J].教育学报,2018,14(2):34-40.
[2]李先东,吴增生.核心素养视角下对数学测评的研究[J].数学教育学报,2017,26(5):36-43.
[3]任子朝,赵轩.数学考试中的结构不良问题研究[J].数学通报,2020,59(2):1-3.
[4]喻平.数学教学心理学[M].北京:北京师范大学出版社,2018:108-111.
作者简介 成鸣娟(1988—),女,陕西渭南人,中教一级,硕士;参与完成两项西安市教育规划课题,主持完成一项陕西省教育规划课题“初中生数学迁移能力的培养研究”,多次被评为“希望杯”全国数学竞赛优秀辅导员;发表多篇论文.

