“比”的历史及其教学启示
王智洋,刘思璐


摘要:从概念产生的角度看,比的意义体现在描述和测量、物物交换、合成与分配、自然与美学四个方面,不仅源自古人对物质生活的需求,还有对精神世界的熏陶。从概念发展的角度看,“比较”“大小关系”和“同类量”是比的定义的“源”,而“除法”“分数”和“非同类量”是比的定义的“流”。比的概念的历史为教学提供了诸多启示:创设教学情境,揭示比的意义;厘清教学主线,阐明比的定义;明晰广度和深度,提升对比的认识;渗透数学文化,达成德育之效。
关键词:HPM;比的意义;比的定义;数量关系
随着越来越多的数学教育工作者意识到数学史的教育价值,HPM(History and Pedagogy of Mathematics的简称,意为数学史与数学教育)研究已经成为数学教育研究的一个重要领域。其中,教育取向的数学史研究是HPM领域的基础性研究,是课例研究的第一步,决定着课例的成败。
“比”是小学数学数与代数学习领域“数量关系”主题下的重要概念,被安排在第三学段(5—6年级)教学。比的知识承接除法、分数的知识,也是学习比例、函数等相关知识的基础。《义务教育数学课程标准(2022年版)》(以下简称“新课标”)要求:“在实际情境中理解比的含义,能解决简单的问题。”比的概念的教学中,學生要理解比的意义,了解比的定义,形成比的概念,即要认识到“为什么要学习比”以及“什么是比”。
现行各版本小学数学教材都通过不同类型的生活情境来体现比的意义。为了选择合适的教学情境,厘清教学主线,实施“发生教学法”,教师需要深入了解比的概念的产生和发展过程。此外,各版本教材上关于比的定义的叙述不尽相同,且较为抽象,给学生的学习和教师的教学造成了困扰。鉴于此,本文拟通过历史文献(包括英美早期数学教科书)的考察,追溯比的概念的产生和发展脉络,为教学提供启示。
一、比的意义的来源
比是数量之间的关系,其意义主要来自四个方面:描述和测量的需要、物物交换的需要、合成与分配的需要以及自然与美学现象。
(一)描述和测量的需要
生活中,各种各样的单位无处不在,我们常用“米”来描述大楼的高矮,用“斤、两”来称量物品的轻重……单位制在我们描述和测量时,发挥着重要作用。事实上,其中蕴藏着比的意义,单位制其实是比的概念形成和发展的最终产物。
最初人们并没有单位的概念,对未知事物进行描述时,只能通过将其与已知事物进行比较来实现。美国数学史家史密斯提到,人类历史早期产生了两个有关比的概念:古人在描述部落规模时,会指出一个部落的人数是另一个部落的两倍多;在形容皮制带子的长度时,会指出一根皮制带子只有另一根的一半长。
随着人类文明的进步,为了建造生活中需要的住房、生产工具等,人们需要对材料的形状、大小等进行测量,自然想到用已有工具的形状、大小等进行测量,这样就得到了最初对长度、重量和容量的度量。苏联学者鲍尔加尔斯基在《数学简史》中介绍了一种传统的长度测量方法——借助人体的部件。 例如,为了测量长度,成年男子的步长被当作最常用的测量单位。如果测量一些体积不大的物体,人们会动用自己的手和脚,将手指的厚度、大拇指关节的长度、手掌的宽度、大拇指与食指或者中指顶端之间的距离等作为测量单位。利用身体的部件进行测量不仅可以较为准确地实现测量目的,还十分便利,随时随地都可以进行。直到今天,我们在生活中依然频繁使用这种测量方法。
之后,由于社会的发展,人们对度量单位的要求更为精确,于是度量单位制度逐渐形成。鲍尔加尔斯基还介绍了古巴比伦建立的公制度量单位制度,其进制是六十。直到今天,依然有六十进制的痕迹存在,如划分时间和角度的方法,即1小时等于60分钟、1°等于60′。这样的度量单位制度能够准确地表达任意的数量,满足商业、农业和建筑业的需要,推动了古巴比伦文明的发展进程,也大大造福了后世。
除了在古代的西方,在古老的中华大地上也建立起了度量衡单位制度,该制度产生于四五千年前的原始社会末期。度量衡是测量长短、容积、轻重的统称,其中“度”指测量长短,“量”指测量容积,“衡”指测量轻重。众所周知,秦始皇统一中国后所做的重要的贡献之一便是统一度量衡。汉承秦制,《汉书·律历志》中有“以一黍之广度之,一为一分”的记载,意思是横排100粒黍的长度记为汉代的一尺(约为今天的23厘米)。书中还详细记载了度量衡的单位、进位以及量器的形状、材质等。这些发明即便在今天,仍不失其耀眼的光辉,在世界度量衡史上也是绝无仅有的。
(二)物物交换的需要
经济的发展离不开生产和交易。在社会分工形成之后,自然产生了以物易物的需求。而在交换过程中,双方为实现公平,必须制订一个交换规则,这便产生了比的意义。
中国汉代数学典籍《九章算术》的第二章《粟米》中记载着以下问题:“若粟率五十,粝米率三十。今有粟一斗,欲为粝米,问得几何?答曰:为粝米六升。术曰:以粟求粝米,三之,五而一。”《粟米》一章主要是为了处理抵押交换的问题,其中用到的方法称为“今有术”,是将所有物的数量乘所有物的率作为分子,将所求物的率作为分母,得到的分数即为所求物的数量,相当于现在教材中解比例问题的“知三求一”。“今有术”涉及比和比例的性质,也揭示了比的概念是在物物交换的过程中产生的。
随着人类文明的进步,货币逐渐产生并充当物物交换的媒介。18世纪出版的英国数学教科书中提到,用一种商品交换另一种商品,或用商品交换货币,或用货币交换商品时,为了使得交易过程更加便利,产生了比的概念。人们可以在一个地方用一笔钱换一张支票,然后在另一个地方将支票兑换成对应的货币,即现在的“外汇兑换”。货币的产生和发展不仅让交易的范围扩大,也极大地增加了交易的便利性和安全性,而这本质上得益于比的概念。
(三)合成与分配的需要
合金产物的硬度和耐用性都高于组成金属,如今已广泛应用于各个领域,其合成的原理也离不开比的概念。早在3000多年前的商朝,中国的青铜工艺就已经非常发达了。公元前6世纪左右锻铸的越王勾践的青铜剑就是一把合金宝剑,出土后仍然锋利无比。斐波那契在《计算之书》的第十一章《论合金钱币的配制》中提到:“当钱币由银和铜混合配制而成时,无论面值多少,它都被称作合金钱币。所谓‘含银2盎司的钱币,意指每磅钱币中含有2盎司的银。”书中介绍了配制合金钱币的三种方法,第一种方法是用一定量的银或铜合铸而成,第二种是由任意给定的钱币加入银或铜合铸而成,第三种是由给定的若干种钱币合铸而成。关于以上三种方法,书中一共展示了七类不同的问题。其中第一类(由给定量的银和铜铸成钱币)如下:“某人有7磅银,欲铸含银2盎司的钱币,他想知道需要加入多少盎司的铜。”解决该问题所用到的方法被称为“商议法(method of negotiations)”,具体过程是:将每磅含银量和含铜量写在第一行,将所有银的数量写在每磅含银量的下方;然后将对角位置的每磅含铜量和所有银的数量相乘,除以每磅含银量,即得所加铜的数量(如下图1所示)。
《论语·季氏》中有云:“不患寡而患不均。”资源和利益的分配是自古以来始终困扰人们的难题。从数学的角度出发,利用除法运算可以平均分配,但是有时,平均分配未必公平。《九章算术》的第三章《衰分》中有这样一个问题:“已知羊吃的食物是马的一半,马吃的食物是牛的一半。问:总共五斗粟如何在这三种牲口间分配?”考虑到羊、马、牛三种动物的差异,平均分配显然不合情理,书中应用“衰分术”解决这个问题。“衰分术”为:将每项之和作为分母,每一项乘分配的总数作为分子,所得的分数即为分得数。本题中,羊、马和牛的食量分别是1、2、4,各项加起来是7,作为分母,将每一项乘以5作为分子,故分给羊、马和牛的粟以斗为单位分别是57、107和207。
(四)自然与美学现象
比的意义除了从生活需求中产生,还蕴藏于奇妙和谐的自然界之中。
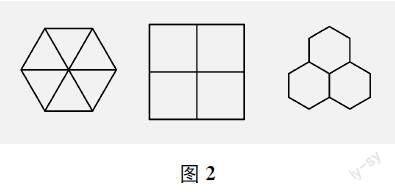
古希腊的毕达哥拉斯学派在悦耳的音乐中,觉察了“和声”,并注意到在用三根弦发音时,如果这三根弦的长度之比为3∶4∶6,就会得到和声的谐音。在许多其他场合,他们也发现了同样的数量关系。例如,立方體的面数、顶点数、棱数分别为6、8、12,它们的比化简后也是3∶4∶6。再如,用正多边形覆盖平面时,只有图2所示的三种情况,所用正多边形的边数分别为3、4、6。根据类似的观察,他们确信,整个宇宙的现象完全依附于某种数值的相互关系,也就是存在着“宇宙的和谐”。
此外,毕达哥拉斯学派还观察到正五角星中有不少黄金比,故视正五角星为神物,将其作为学派的徽章。“黄金比”是意大利著名科学家、艺术家达·芬奇冠以的美称,他在画作中也经常使用黄金比。19世纪末,德国心理学家费希纳做了一个实验:制作了十个长宽比不同的矩形,让592位参观者在其中选择最美的,结果565人认为长宽比为黄金比的矩形是“最美矩形”。可见,黄金比是具有普遍审美价值的。 黄金比揭示了一种和谐的线段比例,因而在古今中外大量的艺术、建筑作品和日常生活中都被广泛应用。
二、比的定义的发展
(一)从国内现行教材中比的定义说起
比就像空气,无处不在,但要具体说出它的定义却是难事。翻开国内主要的几个版本的小学数学教材,有关比的定义的叙述分别如下。(1)沪教版:“a、b是两个数或两个同类的量,为了把b和a相比较,将a与b相除,叫作a与b的比(ratio)。记作a∶b,或写成ab,其中b≠0。a叫作比的前项,b叫作比的后项。 前项a除以后项b所得的商叫作比值。”(2)人教版:“两个数的比表示两个数相除。‘∶是比号。在两个数的比中,比号前面的数叫作比的前项,比号后面的数叫作比的后项。比的前项除以后项所得的商,叫作比值。”(3)苏教版:“两个数相除又可以叫作两个数的比。‘∶是比号,比号前面的数叫作比的前项,比号后面的数叫作比的后项,比的前项除以后项所得的商叫作比值。”(4)北师大版:“两个数相除,又叫作这两个数的比。如,6÷4写作6∶4。6是这个比的前项,4是这个比的后项,1.5是6∶4的比值。”
可见,四个版本教材中,比的定义均基于除法运算,揭示了比和除法之间的统一性。苏教版和北师大版给出的“两个数相除又叫作两个数的比”,意指比和除法是完全一样的,只是名称不同。人教版给出的“两个数的比表示两个数相除”,透露出比的范围相较于除法更宽泛。比、除法以及分数三者之间差异模糊,容易使学生在学习时产生困惑,不理解学习比的必要性。
另外,四个版本教材都规定了比的对象是两个“数”,沪教版教材还补充了两个同类的“量”。同时,人教版教材与苏教版教材采用了“路程与时间之比”的情境,这把比的对象扩大为两个不同类的“量”。
(二)梳理比的定义的发展
比与除法、分数有什么区别?比的对象到底有什么要求?为解决这两个问题,我们翻阅了《几何原本》和大量西方早期教科书。
1.欧氏定义
欧几里得在《几何原本》第五卷中明确给出了比的定义:“当一个较小的量能量尽一个较大的量时,我们把较小量叫作较大量的一部分;当一个较大的量能被一个较小的量量尽时,我们把较大量叫作较小量的倍量;两个同类量彼此之间的一种大小关系叫作比。”
以《几何原本》第五卷命题1的图示(见图3)为例来理解这个定义,EG为较小量,AB为较大量,则EG为AB的一部分,AB为EG的倍量,AB与EG的大小关系为比。
欧几里得认为,比是两个同类量之间的一种大小关系,而这种大小关系特指倍数关系。“量尽”一词,不仅体现了比的“描述和测量”意义,也从“形”的角度帮助我们理解比的概念。《几何原本》中许多命题的图示中都有类似于图3的线段比。
2.比较定义
19世纪的英美教科书基本沿用了《几何原本》中的定义,即比是两个同类量之间的一种大小关系,但叙述更为具体,内容也更加丰富。如J.Day在《代数引论》中写道:
我们经常会把已知的数量与不等于它的其他数量进行比较。那么,如何进行比较?自然就产生了两种比较方式,可以考虑两个数量中一个比另一个多了多少,或者一个是另一个的多少倍。在寻找答案的过程中,我们发现了两个数量的比,分别为“算术比(arithmetical ratio)”和“几何比(geometrical ratio)”。
比是指一个量与另一个量的大小关系。首先这两个量要是相同类型的,否则无法判断。例如,把英尺(长度单位)和磅(重量单位)放在一起比较是荒谬的。
“算术比”表示的比较,旨在发现一个量比另一个量多了多少,即他们的差,最早用“..”表示。a与b的算术比,记为a..b。例如,6..3=3。既然两个量的算术比即两个量的差,而“差”似乎是更好的表达方式。因此,“算术比”逐渐被“差”代替,记号“..”也被“-”代替。“几何比”表示的比较,旨在发现一个量是另一个量的多少倍,简称为比。a与b的比,记为a∶b。例如,6∶3=2。
书中指出比是两个同类量之间大小关系的比较,并交代了两种比较方式——“算术比”和“几何比”,从感知的角度形象地给出了比的定义。
3.形式定义
比的定义叙述在20世纪的英美教科书中发生了较大变化,主要有两种类型:(1)除法定义:“两个数的比是第一个数除以第二个数,通常用a∶b表示,由于比实际上是除法,所以也写成ab。显然,两个不同性质的数量之间没有比,而在同一种类的两个单位之间有比,例如1英尺∶1英寸=12。”(2)分数定义:“两个数a和b的比是分数ab(b≠0)。每两个同类量的比是这些量的数值之比。”
以上两种定义的对象都是两个“数”或两个同类的“量”。其中,除法定义用两个数的除法运算(过程)来定义比,与国内现行教材给出的定义一致;分数定义则从运算结果的角度来定义比。两种定义都表达了比的形式,揭示了比与除法、分數的紧密联系。
(三)厘清比的定义的源流
欧氏定义和比较定义表明,比的“源”是“比较”,是一种“大小关系”,包含了“算术比”与“几何比”两种关系;随着定义的发展,“算术比”逐渐被“差”代替,“几何比”演化成了今天教材中的“比”。这一过程体现了数学是动态发展的,数学追求精确性与严谨性等科学精神。除法定义和分数定义只是“流”,除法和分数是比较大小关系(倍数关系)的一种手段及其结果:可以通过除法对“比”进行运算,得到用分数表示的“比值”。也就是说,关系才是比的内容和本质,除法、分数只是比的形式和现象。比可以推广到三个、四个乃至更多个数量之间的倍数关系,还可以扩展为两个变量之间的函数关系,这些含义较之除法和分数要深刻得多。
关于数和量的关系,数是量的抽象(去掉一切物理属性)。通俗来说,量属于形象具体的现实世界,而数则被抽象到了数学内部,“量=数·单位”。从比的概念产生历程我们可以发现,比来源于生活,即产生于数学外部,所以,比较两个量的大小关系是自然的,由此,同种类型的量成了最直观的前提。随着数学的发展,正如毕达哥拉斯学派提出的“万物皆数”,两个量的比逐渐抽象成了两个数的比,于是两个“非同类量”的比也就能理解了。但与同类量之比不同,非同类量的比值有量纲。也就是说,不仅其数值要比,而且其单位也要比。考虑到数与单位本质上是乘法关系,非同类量的比不能是“算术比”,因为非同类量之间的加减运算(如“1米-1秒”)无论如何都是没有意义的,而非同类量之间的乘除运算(如“1米÷1秒=1米/秒”)可能具有(或被赋予)意义。综上,同类量之比是比的概念之“源”,非同类量之比是“流”,数之比起着纽带作用。从同类量之比到非同类量之比的发展,满足从数学外部到数学内部再到数学外部的顺序,体现了数学来源于生活又应用于生活。
这里值得一提的是,新课标特别强调了计数单位的概念,比如“在理解整数、小数、分数意义的同时,理解整数、小数、分数基于计数单位表达的一致性”(由此就可形成“数=个数·计数单位”的认识),这有助于勾连数和量及其运算的联系,体现数和量及其运算的一致性。
三、教学启示
从概念产生的角度看,比的意义体现在描述和测量、物物交换、合成与分配、自然与美学四个方面,不仅源自古人对物质生活的需求,还有对精神世界的熏陶。从概念发展的角度看,“比较”“大小关系”和“同类量”是比的定义的“源”,而“除法”“分数”和“非同类量”是比的定义的“流”。进一步来看,毕达哥拉斯学派所谓的“万物皆数”指世间万物都可以表示成两个整数之比,但无理数的发现却让其存在漏洞;倘若将“万物皆数”的口号赋予新的含义,改成“万物皆比”,便能将比的意义体现得淋漓尽致。
比的概念的历史为今日教学提供了诸多启示。
其一,创设教学情境,揭示比的意义。阅读有关比的概念的史料,积累丰富的素材,并对多种素材进行分类或加工,可以围绕多个主题创设不同种类的教学情境,从而引导学生归类和总结,揭示比的多种意义。
其二,厘清教学主线,阐明比的定义。学生的认知往往具有历史相似性。若在情境引入中直接采用非同类量的例子,是不符合历史发展规律的,可能会增加学生的困惑。先给出“同类量之比”的定义,再抽象成“数之比”,最后引出“非同类量之比”,这是符合历史发展顺序的教学思路。
其三,明晰广度和深度,提升对比的认识。横向来看,生活中到处都是比,通过情境创设可以让学生感受到数学与生活息息相关。纵向来看,比有着除法、分数所不具备的深刻含义和思想,可以为后面比例、三连比、函数的学习做铺垫。
其四,渗透数学文化,达成德育之效。东西方不同文化背景下比的产生与发展,可以让学生感受到古今中外数学文化的多元性,激发其学习兴趣,树立其动态的数学观。同时,测量、交换、分配等方面的应用,可以让学生感受到数学之于公平要求、理性精神和规则意识等的重要性,数学中蕴含着对美的刻画。

