一类带对数非线性源项的p-Laplace抛物方程解的存在性与爆破
温兰, 杨晗
( 西南交通大学数学学院, 四川成都 611756)
1.引言
本文研究如下带对数非线性源项的p-Laplace抛物方程的初边值问题
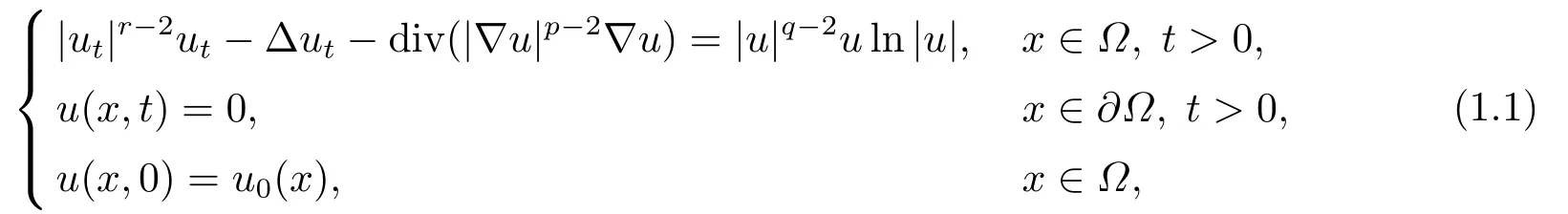
其中r >1, p>2, q >2,u0(x)∈(Ω),Ω是Rn(n ≥1)中具有光滑边界∂Ω 的有界区域.当方程(1.1)中r =2, p=2时, XU和SU[1]研究如下半线性伪抛物方程的初边值问题:
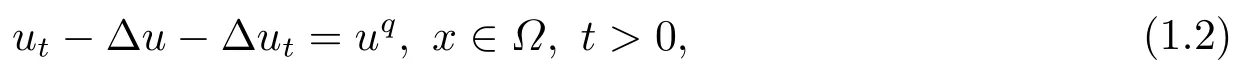
利用势井方法得出方程整体解的存在性并得到解在有限时刻的爆破.近年来, 含对数非线性源项的抛物方程已引起大量学者的研究.CHEN等[2]中研究了带对数非线性源项的伪抛物方程初边值问题:
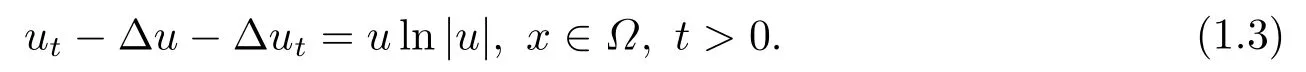
因对数非线性u ln|u|不满足Payne和Sattinger[3]中提出的多项式增长条件, 此时经典势井方法不完全适用.文[2]通过势井方法及对数索伯列夫不等式证明方程整体解的存在性, 并用凸方法证明解在无穷时刻爆破.通过比较得出多项式非线性项对此类伪抛物方程解在有限时刻的爆破有更为重要的影响.随后, 文[4-5]中将上述带对数非线性源项的方程拓展到p-Laplace情形.LE等[5]中研究了如下含对数非线性源项的p-Laplace伪抛物方程的初边值问题:
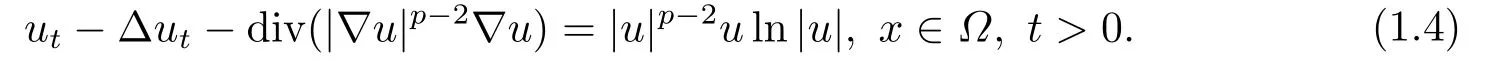
利用势井方法及对数索伯列夫不等式证明了当p > 2时方程整体解的存在性, 并用凸方法得出此时解在有限时刻的爆破.而CAO等[6]中利用Galerkin方法证明了当1 < p < 2时方程整体解的存在性并得出此时解在无穷时刻的爆破.当p-Laplace项与对数非线性项的指数不同时, 对数索伯列夫不等式不再完全适用.文[7-9]中主要研究下述带对数非线性源项的p-Laplace伪抛物方程的初边值问题:
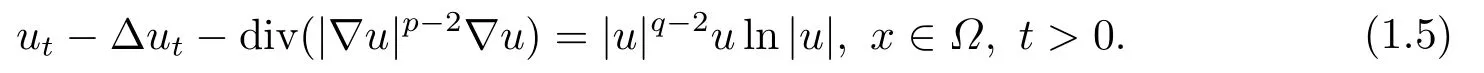
HE等[7]用Galerkin方法证明当2 < p < q < p(1+)时, 方程局部弱解的存在唯一性, 并结合势井方法证明了方程整体解的存在性, 最后得出解的(Ω)范数在有限时刻的爆破.而DAI等[8]对上述结果进行推广主要得出在不同的初始能量下弱解在有限时刻爆破的上界及下界.
对于拟线性情形, Pucci和Serrin[10]中研究如下方程的初边值问题,
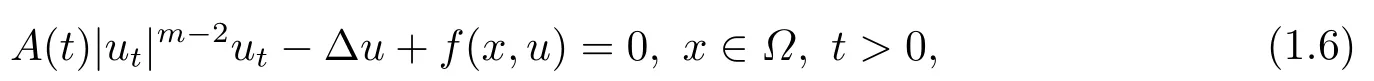
其中m > 1, A ∈C(J →RN×N), f ∈C(Ω×RN→RN)且满足(f(x,u),u) ≥0, 得出方程强解的整体存在性和当t →∞时强解的渐近稳定性.当上述方程(1.6)中f(x,u) = −|u|p−2u时,PANG等[11]中用Galerkin方法证明了当p > 2时初值在稳定集中时方程整体解的存在性, 再通过构造辅助泛函得出当1 基于上述结论, 本文研究方程(1.1)初边值问题, 主要考虑非线性项指数之间的竞争与∆ut项对方程解的存在性和爆破的影响.首先用Galerkin方法证明当非线性项指数满足适当条件时方程局部解的存在性; 然后结合势井方法证明初值在稳定集中时方程整体解的存在性;最后通过构造辅助泛函证明解在有限时刻的爆破. 本文结构安排如下: 第二部分介绍一些符号和引理; 第三部分给出局部解和整体解存在性; 第四部分证明解在有限时刻爆破. 其中N代表Nehari流形, d为势井深度.类似文[7]中引理1和引理2证明可知: 集合N非空, 常数d存在且大于0.由(2.5)和(2.6)可得 定义以下稳定集和非稳定集 下面给出证明过程所需引理, 详细证明过程可参考文[9]. 成立, 则称u 在有限时刻爆破. 这节将给出当非线性项指数满足适当条件时方程(1.1)局部解和整体解的存在性. 由(3.14)-(3.16), 存在T >0, ∀t ∈[0,T]有 由引理2.5并结合(3.17)可得 由此可得 结合(3.25), (3.29)可得χ1=|u|q−2u ln|u|. 设Au = −div(|∇u|p−2∇u), 易证A为严格单调半连续有界的强制性算子(可参考文[12]).则由(3.27)结合单调算子理论可得 由gjm(0)=ξjm, 当m →∞时, u0m强收敛到u0, 因此有 则对于充分大的m, 有 由此可得, 对于充分大的m, um(0)∈W. 下证对于充分大的m, ∀t ∈[0,T], 有um(t)∈W成立. 若不成立, 则存在t0∈[0,T]使得um(t0) ∈∂W, 此时有um(t0) ∈(Ω), 且J(um(t0)) =d或I(um(t0)) = 0.若J(um(t0)) = d, 而由(3.43)得J(um(t0)) < d, 矛盾; 若I(um(t0)) = 0,此时um(t0) ∈N, 由d的定义可得J(um(t0)) ≥d, 显然与(3.43)矛盾.故对于充分大的m,∀t ∈[0,T], 有um(t)∈W成立. 因um(t)∈W, 有I(um)>0, 结合方程(2.5)和(3.43), 对于充分大的m, 有 由此可得 对于任意T >0, t ∈[0,T]成立.再结合定理3.1的证明, 定理3.2得证. 将方程(1.1)两边同乘以u,并在Ω上对x积分,因I(u)<0,结合(2.5)和引理2.3,由Hlder不等式及Young可得 令ε充分小有 注4.1对于J(u0) < 0情形, 在(4.1)中令H(t) = −J(t)同样可得出解的(Ω)范数在有限时刻的爆破, 证明过程大致同上, 在此省略.2.准备工作

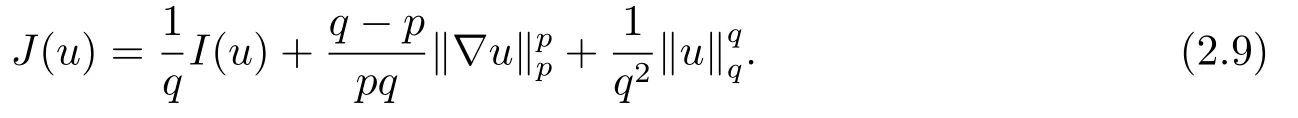
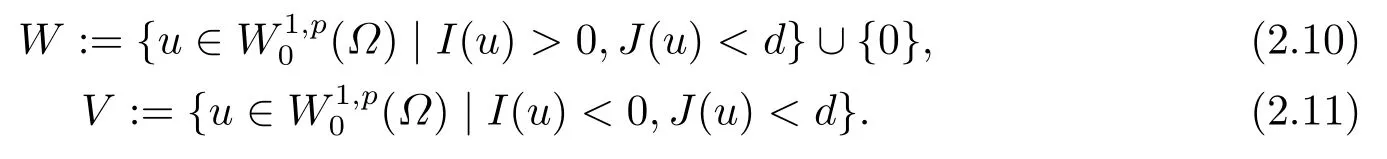

3.解的存在性





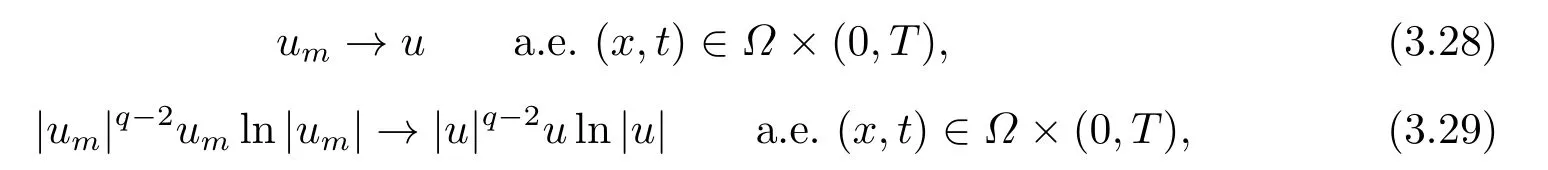

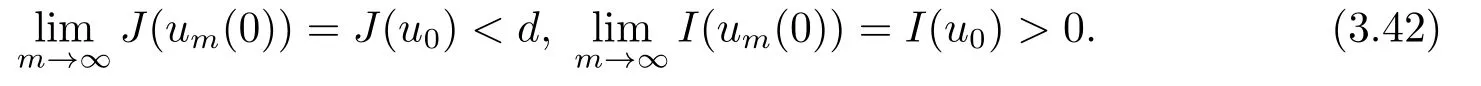
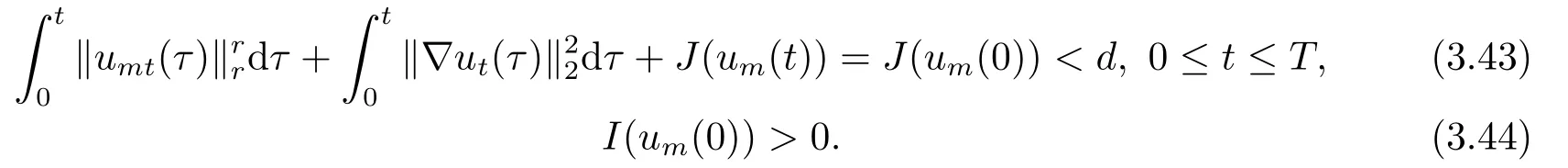
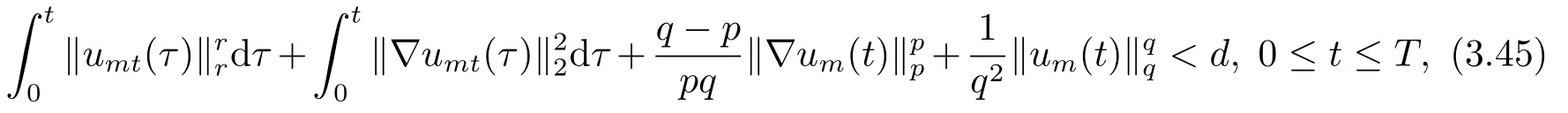

4.爆破