线性半向量二层规划问题的割平面方法

袁梓翠, 吕一兵, 万仲平

(1.长江大学信息与数学学院, 湖北荆州 434023;2.武汉大学数学与统计学院, 湖北武汉 430072)

1.引言

二层规划是一类具有递阶结构的优化问题.由于能够恰当描述实际问题中的层次关系, 二层规划展现出了广泛的应用前景, 同时各种二层规划问题也越来越引起研究者的关注.

半向量二层规划是上层为单目标, 下层为多目标的一类二层规划问题[1].由于半向量二层规划可以较为全面地反映决策者的意愿, 因此越来越引起研究者的关注.

在半向量二层规划问题的最优性条件方面, LIU和WAN[2]利用标量化方法将悲观半向量二层规划问题转化为一个非光滑单层约束优化问题, 同时基于Mordukhovich广义微分, 研究了悲观半向量二层规划问题的最优性条件; Dempe[3]等基于非光滑优化问题的最优性条件, 得出了半向量二层规划问题的一阶最优性必要条件.

在半向量二层规划问题的算法设计方面, 基于线性多目标规划的边缘罚函数方法, 任爱红[4]等将一类半向量二层规划问题转化为带互补约束的单层优化问题, 并在偏静态条件下构造了半向量二层规划的精确罚问题, 并给出了罚函数算法; 刘君娥[5]等利用线性规划的对偶理论,将乐观线性半向量二层优化问题转化为不可微单层优化问题, 通过构建单层问题的松弛问题得到原线性半向量二层规划问题最优值的一个下界; 吕一兵等[6]以下层互补约束为罚项, 构造了线性半向量二层规划问题的罚问题.通过分析罚问题最优解的特征, 设计了一种求解其全局最优解的极点搜索算法; 另外, 吕一兵等[7]以下层问题最优性条件代替下层问题, 进而构造了半向量二层规划问题的罚问题, 并设计出相应的罚函数算法.

值得指出的是, 目前有关半向量二层规划问题的算法研究更多的局限于得到问题的局部最优解.在笔者前期相关研究工作中[6], 设计了线性半向量二层规划问题全局最优解的极点搜索方法, 但是该极点搜索方法需要得到约束域(多面体)的全部顶点.不同于文[6]中的极点搜索方法, 本文将设计线性半向量二层规划问题的割平面方法, 以得到问题的全局最优解.本文所设计的割平面方法的思路为, 首先利用加权法将下层向量优化问题转化为单目标优化问题, 同时基于下层问题的K-K-T最优性条件, 将原问题转化为相应的单层规划问题; 然后通过分析所构造单层规划问题最优解的特征, 同时基于割平面思想, 设计了一种求解线性半向量二层规划问题全局最优解的算法; 最后利用算例对所设计算法的可行性进行分析.值得指出的是, 由于所设计的割平面算法只需求解一系列线性规划问题, 因此具有较好的应用前景.

2.线性半向量二层规划数学模型与预备知识

本文所考虑的线性半向量二层规划问题, 可以表述为,

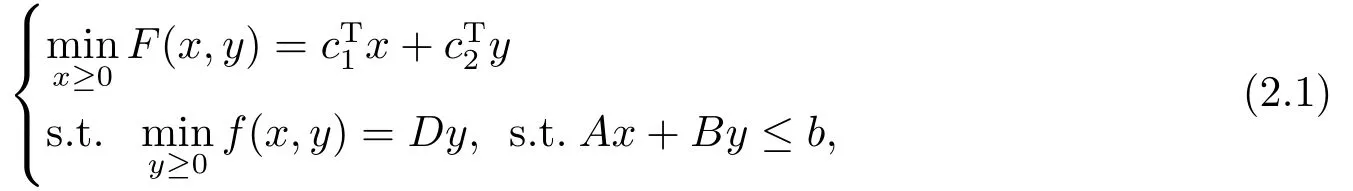
其中, x ∈Rn,y ∈Rm,A ∈Rp×n,B ∈Rp×m,c1∈Rn,c2∈Rm,D ∈Rl×m,b ∈Rp.记z ={(x,y)|Ax+By ≤b,x ≥0,y ≥0} 为上述问题的约束域, T = {x ∈Rn|∃y ∈Rm,Ax+By ≤b,x ≥0,y ≥0}为约束域z 在上层决策空间的投影.对于给定的x ∈T, z(x)={y|(x,y)∈z}为下层问题的可行集.记P(x)为如下下层问题,

的若有效解集.由上述记号,问题(2.1)的可行集可以表述为:IR={(x,y)|(x,y)∈z,y ∈P(x)}.

定义2.1(x∗,y∗)∈IR为问题(2.1)的全局最优解,如果对任意的(x,y)∈IR,有F(x∗,y∗)≤F(x,y).

为了保证问题(2.1)存在最优解, 在接下来的内容中, 假设如下条件成立:

(H1)z为非空紧集, 且P(x)∅.

对于给定的上层决策变量x ∈T, 下层问题(2.2)为线性多目标规划问题.由多目标规划的相关理论[8,9], y为问题(2.2)的若有效解, 当且仅当存在λ ∈Ω =使得y为如下问题(2.3)的最优解,

其中λ为给定的下层目标函数权重系数, 反映了上层决策者对下层各目标的偏好.

值得指出的是, 半向量二层规划问题(2.1)本质上属于下层有不唯一最优解的二层规划问题.对于该类二层规划问题, 其最优解定义一般有“乐观最优解”和“悲观最优解”.在上述问题(2.3)中, λ反映了上层决策者对下层各目标的偏好, 即上层决策者可以影响或支配下层决策者.这就意味着, 本文主要考虑问题(2.1)的“乐观最优解”.

问题(2.3)为单目标优化问题.关于线性多目标规划问题(2.2)的弱有效解集与单目标规划问题(2.3)的最优解集之间的关系, 有如下结果:

命题2.1[8]对于给定的(x,λ) ∈T ×Ω, ψ(x,λ)为问题(2.3)的最优解集, 则有P(x) =ψ(x,λ):=∪{ψ(x,λ)|λ ∈Ω}.

基于上述命题2.1, 可以将问题(2.1)转化为如下问题(2.4),

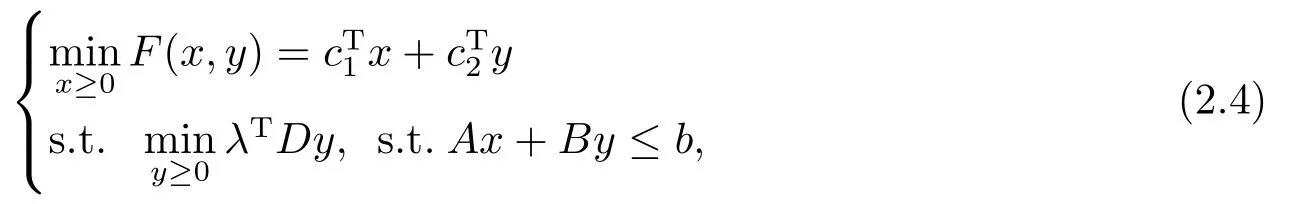
其中, λ ∈Ω为给定的下层目标函数权重系数.

对于上述问题(2.4), 基于下层问题的K-K-T 最优性条件, 可以将问题(2.4)转化为如下非凸、不可微优化问题,

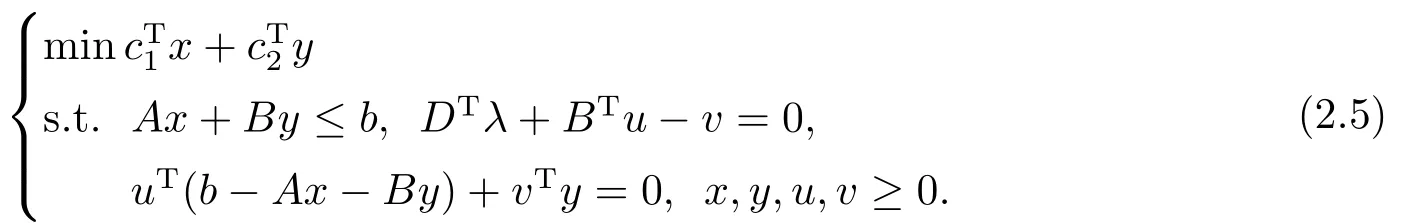
其中u ∈Rp,v ∈Rm为相应的Lagrange乘子, λ为给定的下层目标函数的权重系数.

在下面的内容中, 将着重分析上述单层规划问题(2.5)最优解的相关特征, 同时基于割平面思想, 设计一种求解线性半向量二层规划问题全局最优解的割平面算法.

3.理论与算法

综上所述, 可设计如下求解线性半向量二层规划问题的割平面算法.

割平面算法:

在上述算法中, 引入顶点对应的割平面, 每次割去z中都不含问题(2.1)可行解的部分, 而剩下的部分z1是非退化的多面体; 再从新的约束域出发, 在z1中重复以上步骤.每重复一次都将割去z的一个顶点, 由于z的顶点个数是有限的, 因此经过有限次循环后可以找到一个顶点是原问题的全局最优解.

4.算例

为验证所设计算法的可行性, 利用上述算法求解如下线性半向量二层规划问题[6], 其中x ∈R,y ∈R2.

5.小结

本文研究了线性半向量二层规划问题全局最优解的求解问题.基于线性半向量二层规划问题的最优解可在其约束域的顶点处取得这一特征, 通过构造割平面, 设计了求解其全局最优解的割平面方法.由于所提出算法只需求解一系列线性规划问题, 因此具有较好的应用前景.

值得指出的是, 本文所设计的割平面算法中, 割平面的构造依赖于相邻顶点的获取, 因此如能将高效的多面体相邻顶点的获取方法与本文所设计的割平面方法相结合, 有望极大提升割平面算法的计算效率.