关联调用核心知识 理性构建基本图形①
——一道尺规作图题的解法探究赏析及教学价值导向

陶家友

(江苏省南京市溧水区石湫中学 211222)

2021年南京中考第25题是考察用两种不同的方法过圆外一点作圆的切线的尺规作图题，对于初中学段加强尺规作图的教学进行了很好的评价引领.现将本题的解法探究赏析及教学价值导向呈现如下.

(南京2021年中考第25题)如图1，已知P是⊙O外一点．用两种不同的方法过点P作⊙O的一条切线．

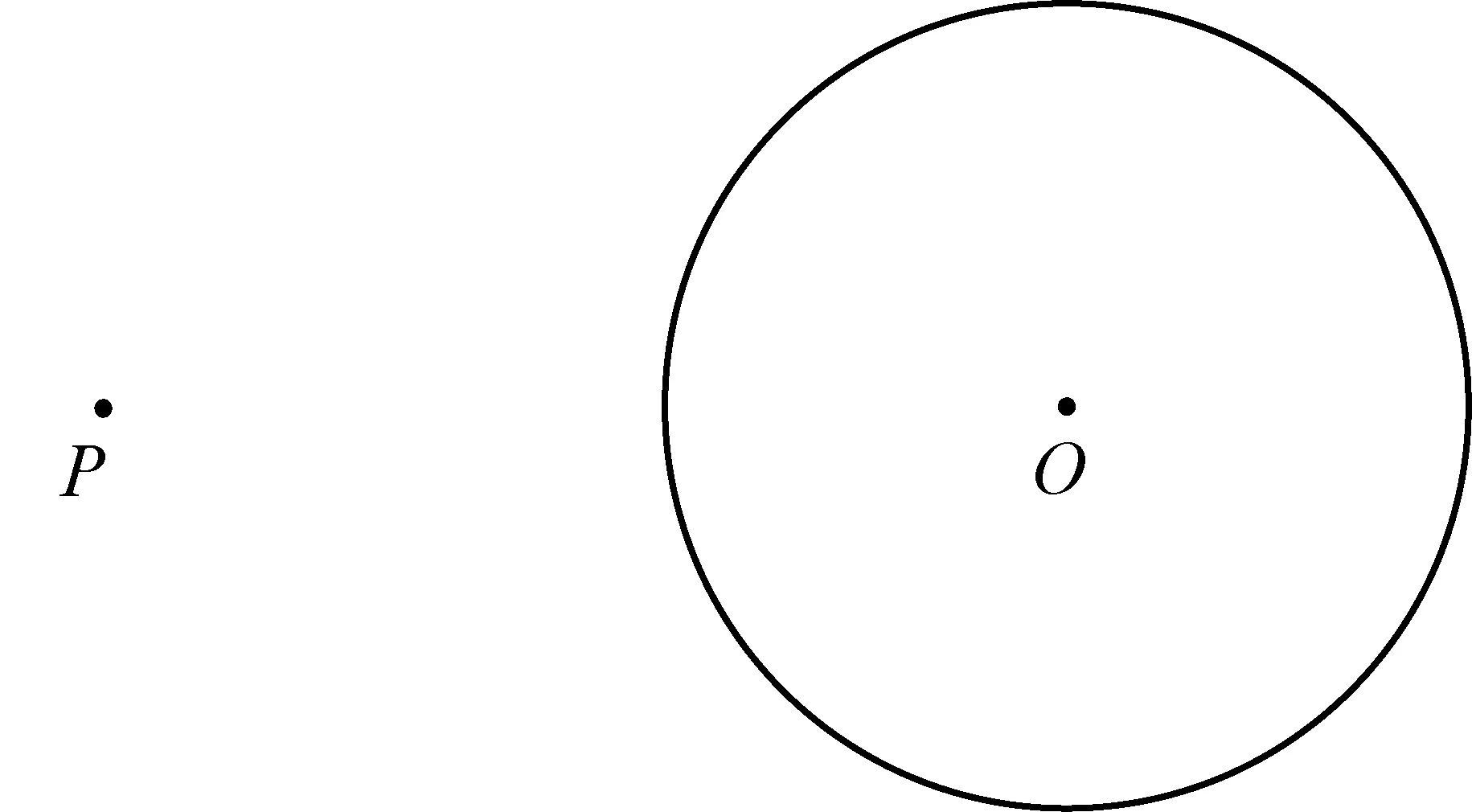
图1

要求：(1)用直尺和圆规作图；(2)保留作图的痕迹，写出必要的文字说明．

1 特色解读

1.1 题目表述简洁，选材背景熟悉，体现人文关怀

作为全卷倒数第3题，学生的第一印象往往是“艰涩”“不易下笔”等，有一些畏难心理.但此题一改常态，题目表述简明，作切线的背景学生也很熟悉， 在学习圆的切线长这一课时，学生经历过从圆外一点作圆的切线的探究活动过程，积累了一些数学活动经验.因此较容易想到本题的一种作法，这样就大大减少了学生心理上的焦虑和恐惧，增加了答题的信心和勇气.较为熟悉的试题能使学生在答题时降低未知因素的干扰，能比较真实地展示出学生的思维水平，有助于稳定学生的考试情绪，增强考试信心，既提升了试题的效度和信度，也传达出命题者对学生的人文关怀.

1.2 解法开放多样，关注核心知识，凸显思维品质

尺规作图题要求保留作图痕迹及必要的文字说明能充分暴露学生思考的方向和推理的路径.本题明确了用尺规从圆外一点作圆的一条切线的作图的要求，但具体怎样作图，学生关联调用自己所熟知的核心知识，理性构建已掌握的基本图形来解决问题.由于不同学生的思维水平以及熟练掌握的模型具有明显的个性差异，因此他们会从不同的角度出发，调用不同的核心知识，给出很多不同的解决方法.

本题的作法具有开放性和多样性，涵盖了初中阶段大部分核心知识，如：等腰三角形、菱形、圆周角、全等及相似、勾股定理、射影定理等，由中考阅卷统计出学生有十几种解答方法，异常精彩；但其中个体差异较大，较多学生只会利用解法1中的核心知识“直径所对的圆周角是直角”来作切线，因此本题对学生的模型思想、综合运用所学知识解决新问题的能力以及学生发散性思维的水平进行了较为充分地考查.

2 解法赏析

学生对尺规作图题的思考过程跟G·波利亚的怎样解题的步骤大致相同，第一步是弄清题意，假设已经作出切线，在纸上作出草图，并在草图上标注已知的量以及要满足的条件，完成对题目的理解；第二步是拟定计划，就是思考怎样去把这个图形确定下来，即要使PQ是圆的切线，就要满足∠PQO=90°，那具备什么条件就可以产生直角尤为关键.学生迅速在头脑里搜索“直角”这个关键词，闪现的“念头”迸发精彩……

2.1 思路1：直接造因法

如何构造产生直角呢？首先思索初中有哪些核心知识或者定理的结论是直角，然后设法满足该定理的题设，从而得到直角的结果，这个种“因”收“果”的思路可称为“造因法”.

解法1利用核心知识“直径所对的圆周角是直角”构造直角．

简析：要使∠PQO=90°，∠PQO的度数及所对得边是确定的，“定边定角”问题学生比较自然联想到用构造直径所对的圆周角来得到直角.

作法：如图2，连接PO，以PO为直径作⊙A，⊙O与⊙A交于点Q，则PQ即为所求作的切线．

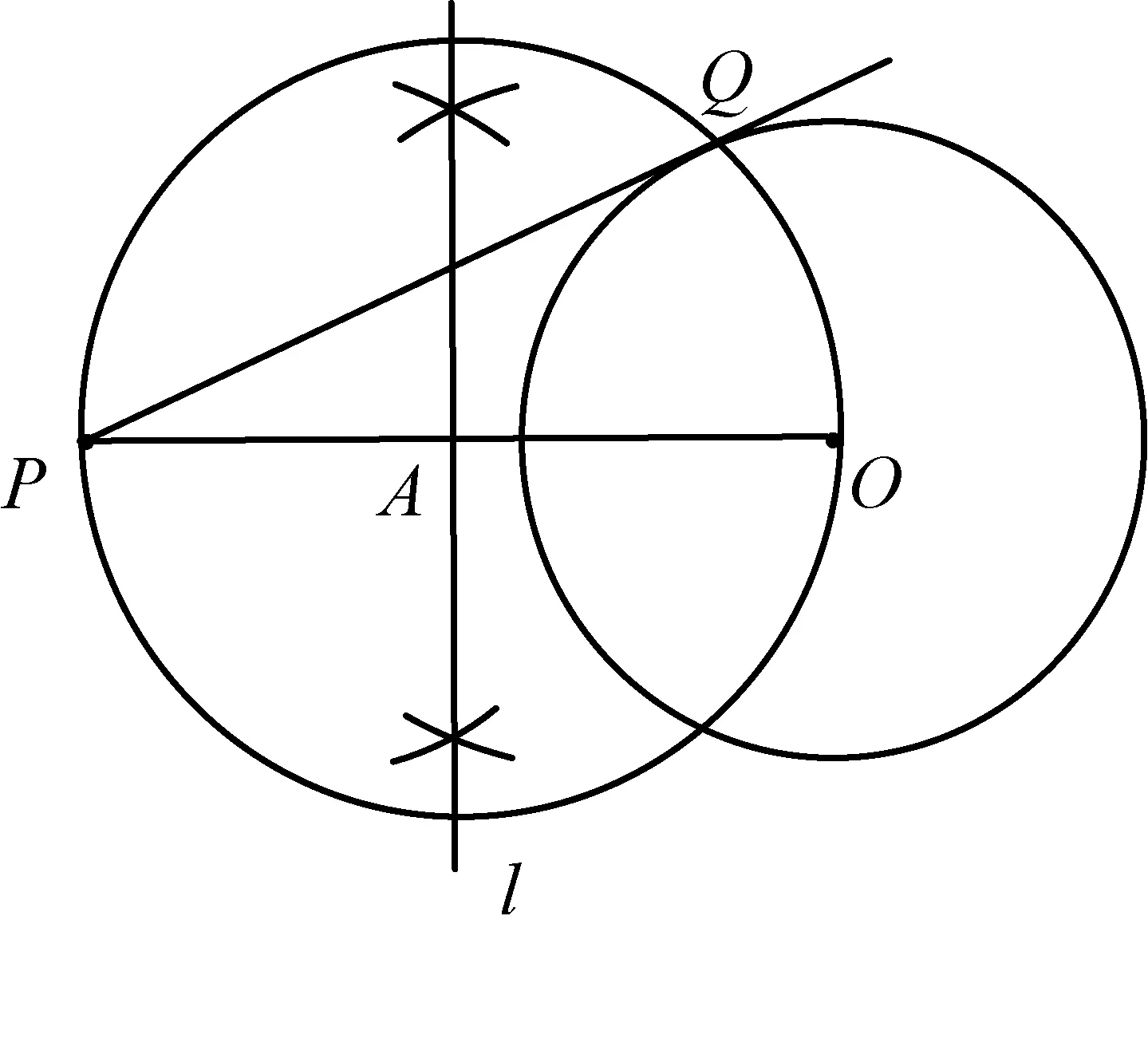
图2

解法2利用常用模型“如果三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形”构造直角．

简析：学生关联熟练掌握的定理“直角三角形斜边上的中线等于斜边的一半”，联想到它的的逆命题是构造直角三角形的常用方法.

作法：如图3，连接PO，作PO的垂直平分线l交PO于点A，以A为圆心，AO长为半径作弧交⊙O于点Q，则PQ即为所求作的切线．

图3

解法3利用核心知识“等腰三角形的三线合一”构造直角．

简析：用“等腰三角形的三线合一”来构造直角是重要且常用的方法.

作法：如图4，以O为圆心，2OA长为半径作弧，以P为圆心，PO长为半径作弧，两弧交于点B，连接OB与⊙O相交于点Q，连接PQ，则PQ即为所求作的切线．

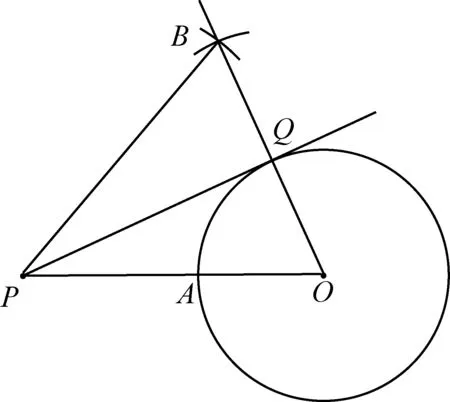
图4

解法4利用核心知识“菱形的对角线互相垂直”构造直角．

简析：关联了等腰三角形之后继续搜索，利用四边形的性质呢？进而想到用“菱形的对角线互相垂直”构造直角．

作法：如图5，以O为圆心，2BC长为半径作弧，以P为圆心，PO长为半径作弧，两弧交于点B，分别以B、O为圆心，PO为半径作弧，两弧交于点C，连接PC、OB相交于点Q，则PQ即为所求作的切线．

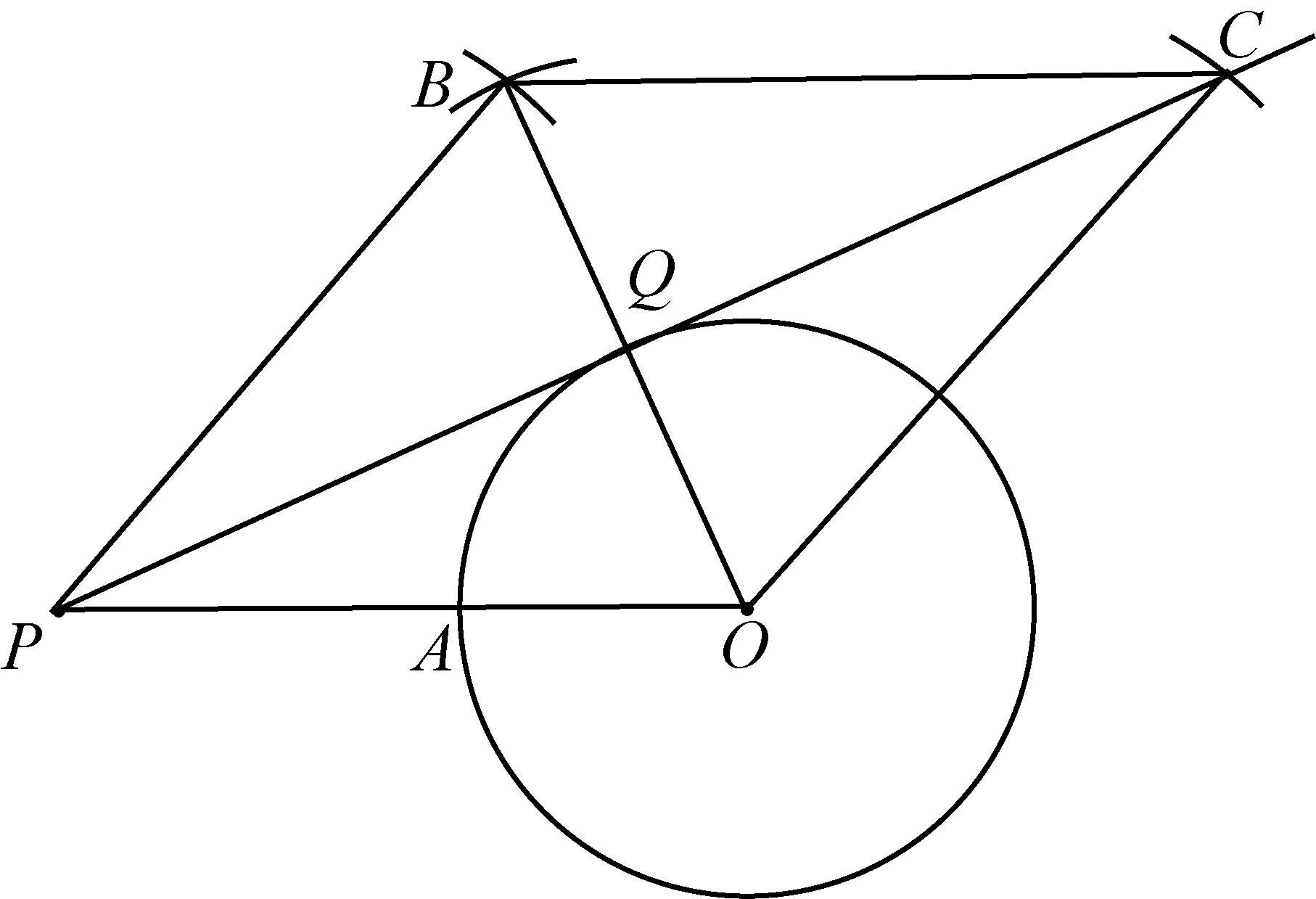
图5

解法3与解法4有什么共同之处？构造的等腰三角形及菱形都是轴对称图形，本质上是利用轴对称的性质：对称点的连线被对称轴垂直平分，那当然也可以构造筝形．

解法5利用常用结论“筝形的对角线互相垂直”构造直角．(作法略)

2.2 思路2：间接复制法

没用联想到相关知识来构造直角，是不是可以先作一个直角，然后在指定位置把直角复制过来？怎么复制呢？尝试通过图形的变换，即用全等或相似的方法.

解法6利用圆现有的点作出直角，再用“全等”在指定位置复制直角．

简析：在PO与⊙O的交点A处作一个直角，结合图形再通过SAS构造“镖形”全等来巧妙地复制直角.

作法：如图6，连接PO交⊙O于点A，过点A作l⊥OP，以O为圆心，OP长为半径作弧交l于点B，连接OB交⊙O于点Q，连接PQ，则PQ即为所求作的切线.

图6

解法7利用圆上任意一点作出直角，再用“全等”在指定位置复制直角．

简析：由解法6追问：为什么一定要在点A处作直角呢？其它任意一点也可以吗.这样具有一般性，更为本质.“镖形”全等演变为“旋转型”全等或“轴对称”全等.

作法：如图7，在⊙O上任取点A，连接OA，过点A作l⊥OA，以O为圆心，OP长为半径作弧交l于点B，连接OB，作∠POQ=∠BOA，OQ交⊙O于点Q，连接PQ，则PQ即为所求作的切线．

图7

解法8利用“相似”复制直角．

简析：既然通过全等变换可以复制直角，那通过相似是不是也可以呢？先构造以2PO为直径所对的圆周角来得到直角，再通过位似复制直角.

作法：如图8，以O为圆心，OP长为半径作圆，连接PO并延长分别交小圆大圆于点A、B、C，以C为圆心，AB长为半径作圆交大圆于点D，过点O作OQ⊥PD交PD于点Q，连接PQ，则PQ即为所求作的切线．

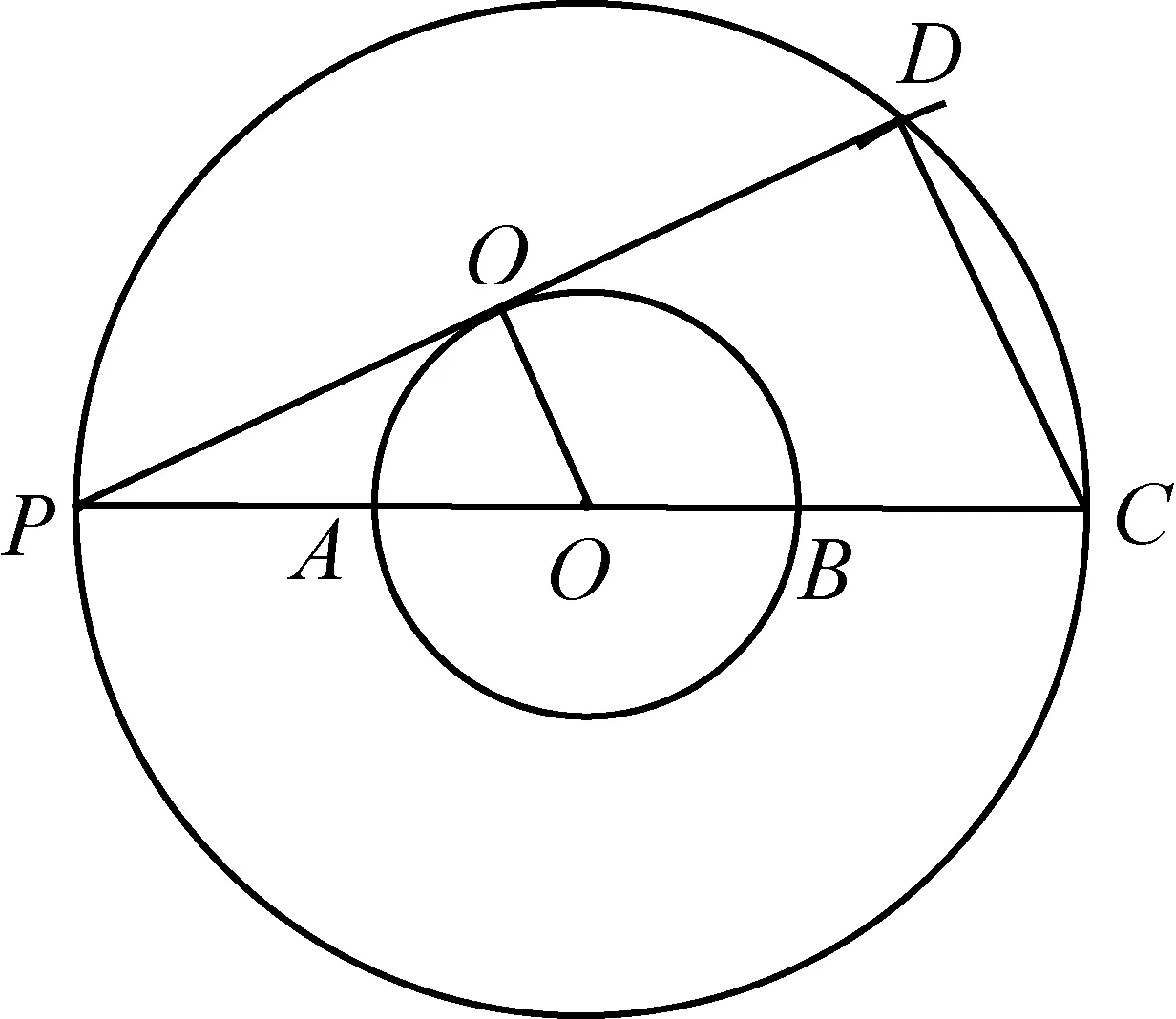
图8

解法8通过位似放大来构造直角，当然通过位似缩小也可以.

2.3 思路3：定量刻画法

解法9利用核心知识勾股定理直接确定切线长．

简析：在作法探析中，从“确定”的眼光审视Rt△POQ，⊙O的半径确定、点P的位置确定，从而PO的长度确定，根据勾股定理得出切线长PQ也确定，

作法：如图9和10，作∠BMC=90°，在MB上截取MD=OA，以D为圆心，OP长为半径作弧，交MC于点E．以P为圆心，ME长为半径作弧交⊙O于点Q，连接PQ，则PQ即为所求作的切线．

图9

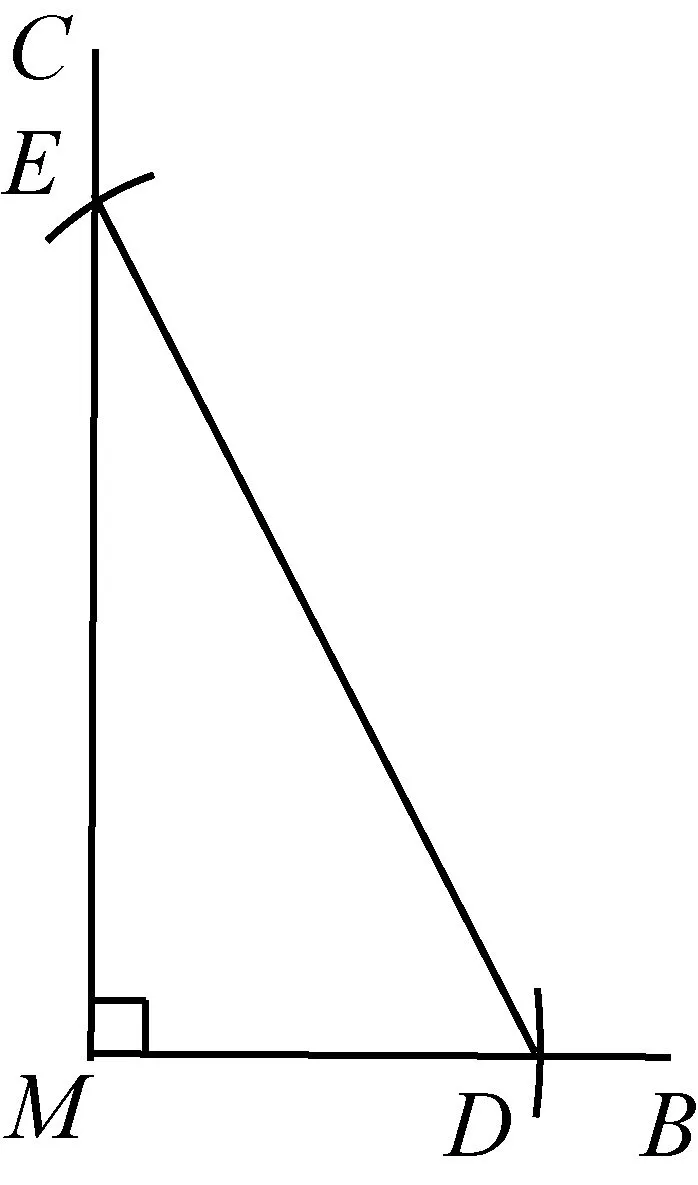
图10

解法10利用核心知识射影定理和切割线定理确定切线长．

简析：切线作法探析过程中，除了想到直角，还能自然联想到什么基本图形？常见的切割线的图形不难想到，那又如何根据割线来确定切线呢？构造射影定理的念头自然迸发.

作法：如图11，连接PO，并延长分别交⊙O于点A、B，以PB为直径作⊙M，过点A作AC⊥PB交⊙M于点C，连接PC，以P为圆心，PC长为半径作弧交⊙O于点Q，连接PQ，则PQ即为所求作的切线．

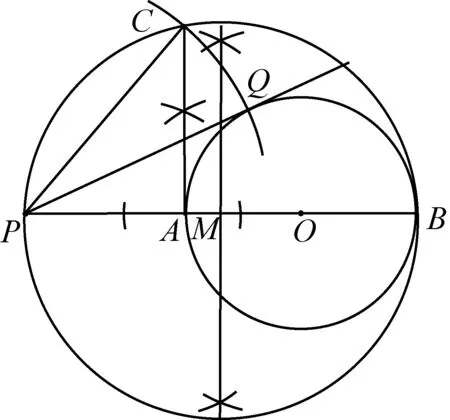
图11

学生大多作出了过圆心的割线，那任意一条割线也是可以的，更具一般性.

解法11利用“全等”确定点和圆心连线与切线的夹角．

简析：解法9从“确定”的眼光通过勾股定理确定切线长，那图中还有哪些量确定，能不能换个思路？容易想到确定的直角三角形中不但边确定，角也是确定的.因此只需确定点和圆心连线与切线的夹角即可.

作法：如图12和13，作∠BMC=90°，在MB上截取MD=OA，以D为圆心，OP长为半径作弧，交MC于点E．以P为顶点作∠OPQ=∠MED，则PQ即为所求作的切线．

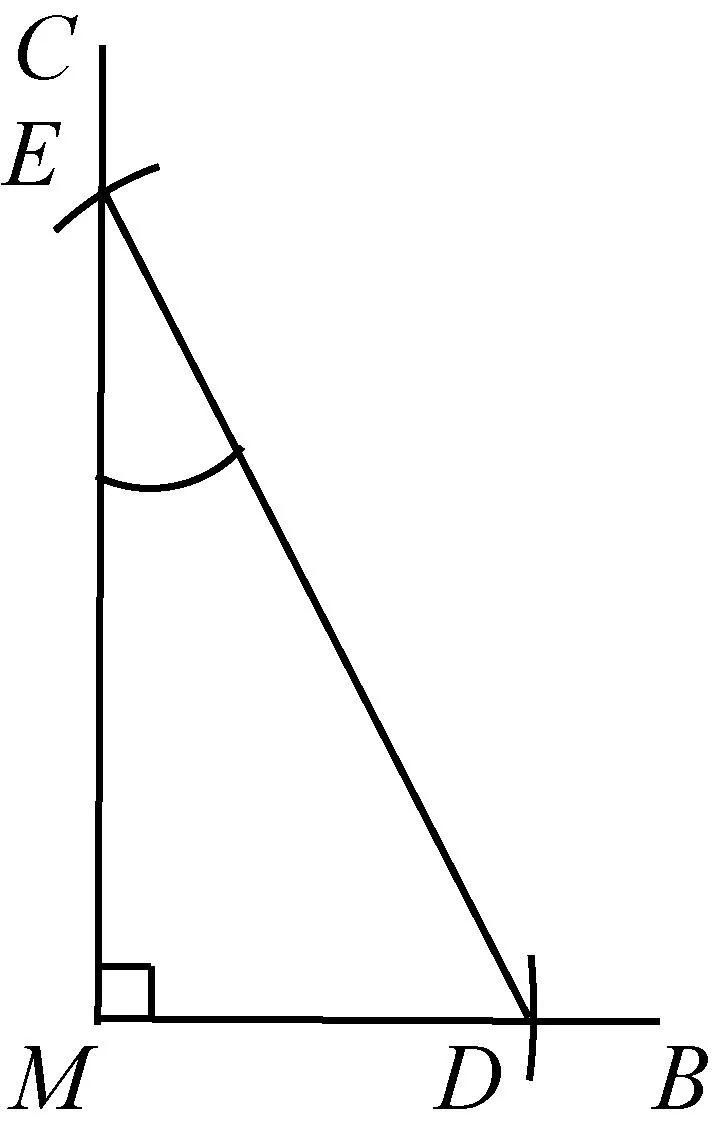
图13

3 教学导向分析

本试题突出对尺规作图的背后的思维品质的考查，虽然作法丰富多彩，但通过阅卷反馈，学生解答并不理想，没有达到我们的预期，甚至有不少学生连一种方法都难以作出，8分的作图题均分却没能达到3分，这不禁激起我们反思尺规作图教学的现状并进行理性思考.

3.1 剖析尺规作图存在问题

(1)机会较少，方法不多

从圆外一点作圆的切线是在学习圆的切线长这一课时，会自然经历的尺规作图，也是很好的通过尺规作图来发展学生发散性思维和数学推理能力的机会，但阅卷暴露出不少学生甚至连一种方法都难以完成，究其原因就是教师为了快速得出切线长定理，仅仅让学生草草画出作圆的切线的示意图，剥夺了让学生自主探究尺规作图方法的好机会，或者虽然让学生尺规作图，但得出一种最常用的方法就鸣金收兵，作法单一，错失了探究作法多样性的机会.

(2)作前不析，直接告知

由于现行教材中尺规作图的内容的呈现方式较多采用程序性操作，例如五种基本尺规作图等简单作图，多数教师在教学时，作图被弱化为一种操作，往往直白地告知作图步骤，然后当成技能训练去反复强化，却很少让学生主动探索分析作图方法，剥夺了学生经历分析条件、主动关联、调用模型、构建图形的完整思维过程.导致学生对作图原理认识不足.很遗憾没有在作图的起始阶段将尺规作图过程中蕴含的数学思想进行外化.

(3)作后不证，不重说理

尺规作图是隐去书写过程的解题，但不写过程，不代表没有思维过程，现实是作图完成后，很多教师并不注重引导学生进行说理，而是开始找大量练习训练学生作法的熟练程度，这样会加剧学生不重“理”的现象，久而久之还会造成学生胡乱“造”图的现象，作图后证明说理既是数学严谨性的体现，又是作图思维的价值所在，不可或缺.

3.2 认识尺规作图教学价值

尺规作图，以开放发散的思路、几何直观的方式、思维严谨的逻辑成为数学教学中蕴含思维价值的教学内容.本试题一方面突出考查了尺规作图的背后的思维品质，又直面当前尺规作图教学存在问题，很好地为教师指引尺规作图教学的方向.尺规作图具有如下教学价值：

(1)发展学生发散性思维

本题中作圆的切线关键就是构造直角.在作法思路的探析时，不同的学生会关联调用他最熟悉的核心知识和经验来推理构造直角，基于不同的“理”就会诞生不同的“图”、不同的“法”，从而迸发出丰富精彩的作图方法.有“直接造因法”、“间接复制法”、“定量刻画法”.这不但为不同思维层次的学生提供了探究空间，同时自己创造及与他人合作交流得到的多种方法，有利于发张学生的发散性思维，激发探究的兴趣，培养学生的创新能力.

(2)发展学生几何直观能力

借助几何直观，可以把复杂的数学问题变得简明形象，有助于探索解决问题的思路，预测结果.学生在作图过程中，首先是头脑中想象目标几何图形，然后画出示意图，再根据直观的示意图厘清图形中的数量和位置关系，因此尺规作图是发展学生几何直观能力的好载体.

(3)发展学生数学推理能力

尺规作图补在是机械的作法，它蕴含了独特的思维和严谨的推理.其中的推理包含两部分.一部分是作法探析时的思考过程，以解法7为例，目标切线如何得到的？怎样构造直角？可尝试通过弱化条件，先过圆上任意一点作出切线，得到直角，然后再通过构造全等复制到指定位置，那又如何构造全等？哪些边角要素已经确定， 哪些要素还无法直接确定？虽然无法直接确定的要素，但有怎样的条件限制？怎样去满足这样的条件……这样的作法分析过程本质上就是严谨的推理过程.另一部分是作图完成后的说理证明，以确保作出图形是正确的.无论是作法的思路探析还是正向证明都需要学生调用所学核心知识、活动经验进行推理，凸显了作法背后的“理”与“法”，充分发展了学生的推理能力.

3.3 加强尺规作图探究引导

(1)重视尺规作图 增加作图机会

尺规作图，以开放发散的思路、几何直观的方式、思维严谨的逻辑成为数学教学中蕴含思维价值的教学内容.本试题一方面突出考查了尺规作图的背后的思维品质，又直面当前尺规作图教学存在问题，很好地为教师指引尺规作图教学的方向.尺规作图具有发展学生发散性思维、几何直观、数学推理能力的教学价值.

因此要重视尺规作图的教学，在日常教学中要适时增加尺规作图的机会，可以是在定理的探索过程中，例如本试题就不容错过；可以在命题理解过程中，例如，在学习“边边角”无法判定三角形全等时，可以引导学生作图感受“边边角”一般有两种情况；也可以在问题解决过程中，例如，以一个角为基础，用尺规作图画一个平行四边形，并说明理由.学生在作法探析过程中，需要关联调用平行四边形的判定定理；当然还可以进行尺规作图微专题的解题教学，例如“过点切边”类的尺规作图及变式探究.

(2)选好作图素材 开放课堂探究

本试题取材源自教材，源于课堂教学，在学习切线长定理引入时，就可以设计自然的问题：过一点画圆的切线可以画几条？请用尺规作图画出.学生首先要对点与圆的位置关系进行分类，从过圆内一点不可以作切线，到过圆上一点可画一条切线，再到过圆外一点可作两条切线，学生的思维自然有序，接下来探究“有内涵但不复杂”的过圆上一点画切线，其作法也是丰富多彩，最后在已有活动经验上类比探究“更有思维含量”的过圆外一点作切线.

试题要求用两种不同的方法作切线，旨在考察学生发散性思维及解决问题方法的多样性.中考阅卷反馈情况并不理想，甚至不少学生连一种方法都没想出，深刻反思平时尺规作图教学，为什么想不到？究其根本原因，是我们的尺规作图课堂教学时直白告知，封闭单一，得出一种方法就大功告成，鸣金收兵.因此，教师要精心选取作图素材，设计适切的问题活动，始终坚持“学为中心”的理念，多给学生探究的时间和空间去思考探究作法，让学生大胆地表达自己的“念头”，而不是去揣度教师期望的标准答案，教师要具有一双慧眼，及时关注学生在作法探析过程中面临的思维障碍和困难，捕捉学生暴露出真实的、自然的、有价值的原始思维，正如全国知名中考命题专家王红兵老师倡导的以学定教，顺学而教，教师分步适时介入.通过点拨及追问，激发学生主动关联调用相关核心知识，并将其整体化、经验化、结构化，理性构建基本图形来获取解决问题的思路，潜移默化地达到了深度学习，这样开放的探究课堂上才会不断迸发精彩，高潮迭起.

(3)基于通性通法，追求解法自然

本试题的解法众多，大多方法是基于核心知识的关联提取以及模型思想自然运用，着重过程与方法目标的考察，这就要求教师在学生“愤悱”之时，必须要“逼”他们充分体验结果“若隐若现”的“痛苦”，就差一口气出不来；然后在老师的“撩拨”之下“踏破铁鞋无觅处，得来全不费功夫”；最后学生之间主动相互“撩拨”，点到为止再思考，“心有灵犀”交流共享自己创造的独特解法，进而感受解法探究的“欲罢不能”.

张景中院士认为：小巧一题一法，不应提倡，大巧法无定法，也确实太难，出路在于中 巧.这里的中巧，指的就是数学解题中有章可循的通性通法.教师应加强通性通法的指导，力图外显一般化的思考方法，引领学生形成一般化的思维习惯和自主探析作法的能力.正如苏步青数学教育奖、生长数学倡导者、设计者、探索者、实践者卜以楼老师所追求的营造前后一致，逻辑连贯，一以贯之的生长性思维.我们倡导发散性思维，并不是刻意追求解法越多越好，而是引导学生主动自觉地用通性通法探究解法，实现最近联想的自然性.其实本试题还有如图14，15的“三条割线”、“两双割线”这样仅用无刻度直尺作图的方法，但这样的解法既想不到，也不会证明，对学生的思维发展的价值很小，如果有点价值，那就是学生惊叹其神奇，有点兴趣而已.相较于一题多解，方法的归纳梳理有助于提升思维品质.

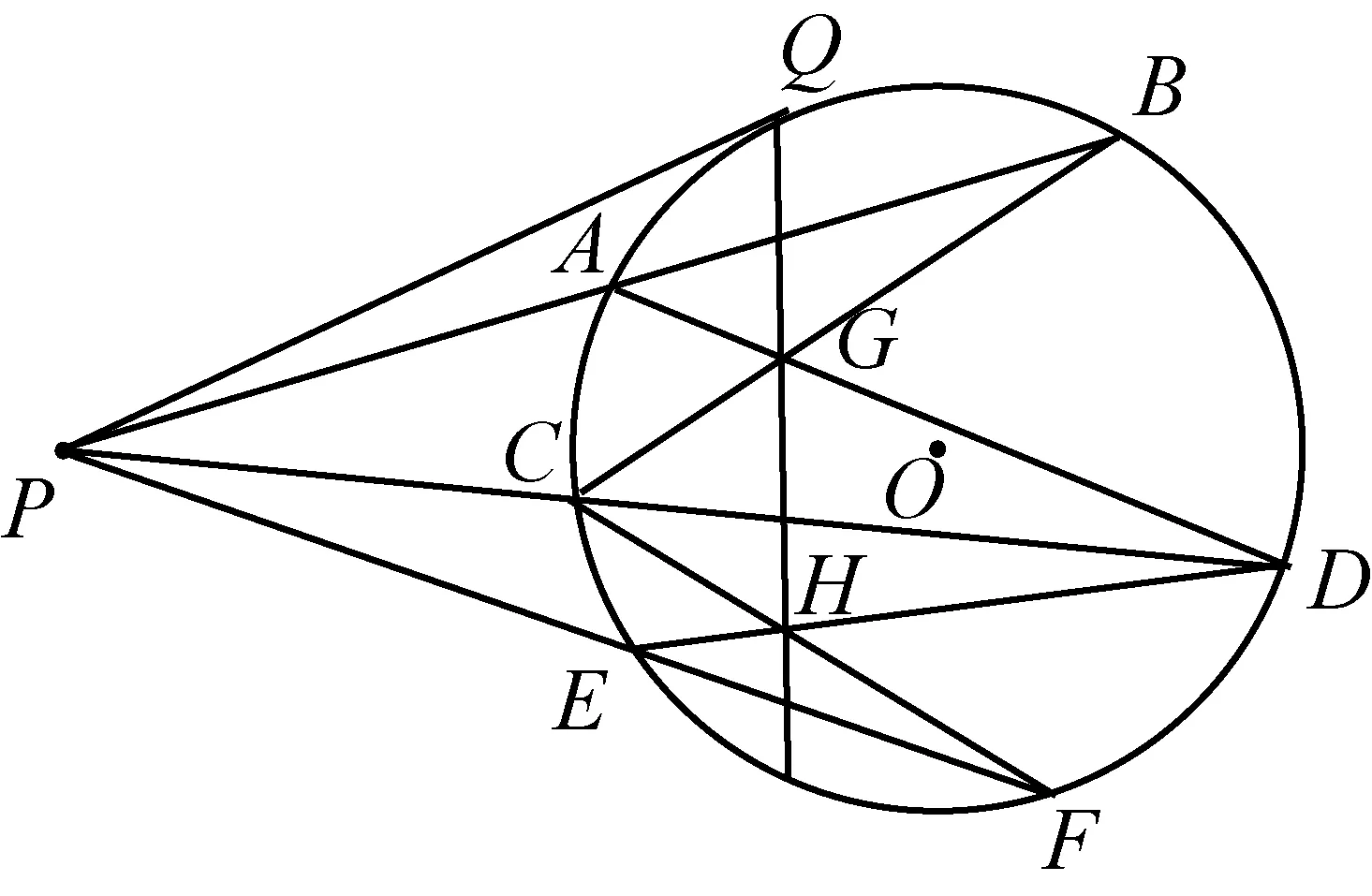
图14

图15

尺规作图教学应引导学生去分析思维的起点与突破口，寻找朴素的适合学生思维的自然，坚持前后一致的必然，揭示揭示本质贯通的超然.即首先要让学生“想得到”，知法明理，再让学生“想得妙”，优化思维.教给学生作法背后的“套路”，感悟“套路”背后所蕴含最基本的思想方法，最后让学生“想得透”，让通性通法成为学生作图的“家常菜”，从而真正提高学生的数学素养.