复合函数巧求导 精设结构妙成章
——对二次曲线切线方程原创性方法的论证

武汉大学附属中学 杨宏齐 齐黎明 袁 明

1 预备知识

图1

2 关于圆的切线方程

(1)过圆上一点的切线方程

已知圆C方程为(x-a)2+(y-b)2=r2，若P(x0，y0)在圆上，则过点P的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2；若P(x0，y0)在圆外，过P作圆的两条切线PA，PB，则切点弦AB所在直线的方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.

图2

如图2，P(x0，y0)为圆C上一点，过点P的切线为l，则CP⊥l.

设直线l：(x0-a)(x-a)+(y0-b)(y-b)+c=0，又l过点P(x0，y0)，且点P(x0，y0)在圆C上，则(x0-a)2+(y0-b)2+c=0，所以c=-r2.

故过圆上一点P(x0，y0)的切线l的方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.

(2)过圆外一点的切点弦方程

图3

如图3，P(x0，y0)为圆C外一点，过点P作圆C的两条切线PA，PB，其中A(x1，y1)，B(x2，y2)，可知直线PA，PB的方程分别为

(x1-a)(x-a)+(y1-b)(y-b)=r2；

(x2-a)(x-a)+(y2-b)(y-b)=r2.

又因为点P(x0，y0)在直线PA，PB上，所以，

(x1-a)(x-a)+(y1-b)(y-b)=r2，

(x2-a)(x-a)+(y2-b)(y-b)=r2.

由此可知点A，B均在直线(x-a)(x0-a)+(y-b)(y0-b)=r2上.

所以切点弦AB所在直线的方程为

(x-a)(x0-a)+(y-b)(y0-b)=r2.

特别地，当圆心在原点，圆C的方程为x2+y2=r2时，有以下两个结论：

①若点P(x0，y0)在圆C上时，则过P(x0，y0)的切线方程为xx0+yy0=r2；

②若点P(x0，y0)在圆C外时，过P可作两条切线PA，PB，则切点弦AB所在直线的方程为xx0+yy0=r2.

3 关于椭圆的切线及切点弦所在直线方程

(1)过椭圆上一点的切线方程

受过圆上一点切线方程推导的启发，可以先通过求导求切线的斜率，进而得到切线的法向量，切线方程设出精巧结构，便于后面代点.

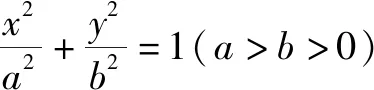
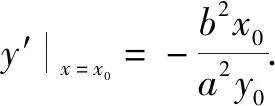
由点(x0,y0)在切线上，可得m=1.

因此，过椭圆上一点P(x0,y0)的切线方程为

如果点P(x0,y0)在坐标轴上，很容易检验符合上式.

(2)过椭圆外一点的切点弦方程

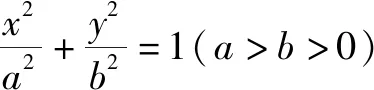
4 关于双曲线的切线及切点弦所在直线方程

5 关于抛物线的切线及切点弦所在直线方程

所以可取切线的法向量为(p,-y0)，切线方程可设为px-y0y+c=0.

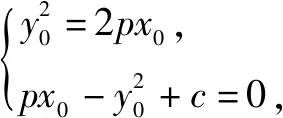
所以，过抛物线上一点P(x0,y0)的切线方程为

y0y=p(x+x0).

若P为顶点(0，0)，切线符合上式.同理可以推证抛物线切点弦所在直线方程为y0y=p(x+x0) .

例1过点P(1，-2)作圆C：x2+y2=1的两条切线，切点分别为A，B，则直线AB的方程为( ).

解析：切点弦AB所在直线的方程为x·1+y·(-2)=1，即x-2y-1=0.故选：D.

变式(2021秋·开福区校级月考)已知圆x2+y2=25，则过圆上一点A(3，4)的切线方程为( ).

A．3x+4y-25=0 B．4x+3y-24=0

C．3x-4y+7=0 D．4x-3y=0

解析:切线方程为x·3+y·4=25，即3x+4y-25=0.故选：A.

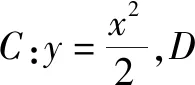
(1)证明：直线AB过定点；

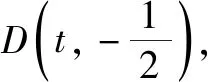
第(2)问略.

以二次曲线为背景，通过深入研究切线及切点弦问题[1]，培养学生发现问题、提出问题、解决问题的能力.根据上述几点结论，让学生感受切线及切点弦问题[2]的丰富内涵以及突破高中数学中切线及切点弦问题的多种途径.