量化核最小逆双曲正弦自适应滤波算法*

火元莲 脱丽华 齐永锋 张印

1)(西北师范大学物理与电子工程学院,兰州 730000)

2)(西北师范大学计算机科学与工程学院,兰州 730000)

针对非线性问题,本文将核方法和双曲正弦函数的逆相结合,提出了鲁棒的核最小逆双曲正弦算法.然后利用向量量化对输入空间数据进行量化,构建出能够抑制网络规模增长的量化核最小逆双曲正弦算法,降低了原有算法的计算复杂度,给出了量化核最小逆双曲正弦算法的能量守恒关系和收敛条件.Mackey-Glass短时混沌时间序列预测和非线性信道均衡环境的仿真结果表明,本文所提出的核最小逆双曲正弦算法和量化核最小逆双曲正弦算法在收敛速度、鲁棒性和计算复杂度上具有优势.

1 引言

在过去的几十年中,核方法已经成功的应用于自适应滤波领域来解决非线性问题.核自适应滤波器[1](kernel adaptive filter,KAF)使用Mercer核[2],将数据从输入空间映射到再生核希尔伯特空间(reproducing kernel Hilbert space,RKHS).在再生核希尔伯特空间中,通过计算所谓的内核技巧[1],可以很容易地计算出内积.核自适应滤波算法在解决非线性问题和非线性信道均衡方面优于普通的自适应滤波算法.核自适应滤波算法主要有:核最小均方(kernel least mean square,KLMS)[3]算法、核最小平均p范数(kernel maximum meanp-power,KLMP)[4]算法、核最小lncosh(kernel least lncosh,KLL)[5]算法、核最大相关熵准则(kernel maximum correntropy criterion,KMCC)[6]算法以及一些改进算法.这类算法的主要缺点是径向基函数网络随着新数据样本的增加而增长,从而增加了计算复杂度,需要更多的内存.针对其问题,研究者们采用了各种稀疏化方法来抑制网络增长,稀疏化数据的方法主要有近似线性依赖性(approximate linear dependency,ALD)准则[7]、惊奇准则(surprise criterion,SC)[8]、新颖性准则(novelty criterion,NC)[9]和预测方差准则[10]等.稀疏化方法可以减少网络规模的增长,但在稀疏化过程中要丢弃冗余数据,从而降低了滤波精度,因为这些数据也在参与网络系数的更新.向量量化(vector quantization,VQ)[11]被用来解决该问题,并已成功应用于当前的核自适应滤波算法,它的主要思想是通过量化来压缩输入空间,以抑制网络规模的增长.文献[12]提出了量化核最小均方算法(quantized kernel least mean square,QKLMS)算法.文献[13]通过改进核递归最小二乘(kernel recursive least squares,KRLS)算法,提出了量化核递归最小二乘(quantized kernel recursive least squares,QKRLS)算法.文献[14]利用最大相关熵准则(maximum correntropy criterion,MCC)[15,16]算法,为脉冲噪声环境下的非线性系统模型,提出了量化核最大相关熵准则(quantized kernel maximum correntropy criterion,QKMCC)算法.

文献[17]利用双曲正弦函数的逆构造了新的代价函数,并证明了该自适应滤波算法在非高斯环境下的性能表现良好.受此启发,本文将双曲正弦函数的逆放到再生核希尔伯特空间中,构造了核最小逆双曲正弦(kernel least inverse hyperbolic sine,KLIHS)算法.同时为了进一步降低该算法的计算复杂度,利用向量量化方法来抑制其网络规模的增长,提出了量化核最小逆双曲正弦(quantized kernel least inverse hyperbolic sine,QKLIHS)算法,并研究了QKLIHS 算法在Alpha 稳定分布环境[18−20]下的非线性信道均衡[21]问题和Mackey-Glass 短期混沌时间序列预测[22]问题中的性能.仿真结果表明,KLIHS和QKLIHS 算法在收敛速度和稳态误差方面比KLMS,KMCC,KLMP,KLL和QKLMS算法有更好的性能.

2 量化核最小均方算法

核技巧就是将任意核从输入空间U映射到特征空间F的一种方法,基于Mercer 定理,其可以表示为

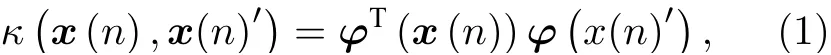
其中x(n)表示输入信号在n时刻的值;x(n)′表示输入信号在下一时刻的值.本文采用核宽为h的高斯核,表示为

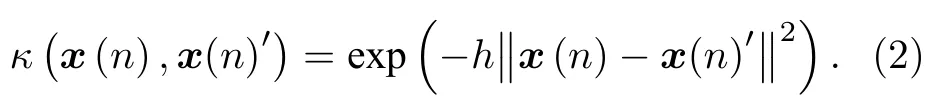
QKLMS 算法是由KLMS 算法应用量化方法得到的.KLMS 算法的权值更新方程可以写为

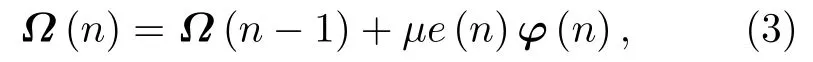
其中Ω(n)是权重向量;µ是步 长;e(n)=d(n)−ΩT(n −1)φ(n)是n时刻的预测误差;d(n)是期望信号;φ(n)是核自适应滤波器输入.

用量化方法量化φ(n),则QKLMS 算法的权值更新方程可以写为

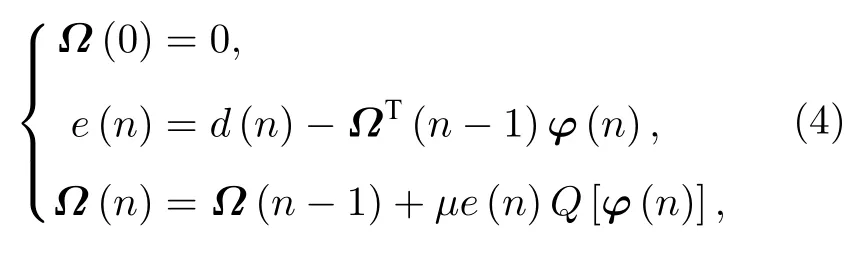
其中Q[·] 表示在高维RKHS 中的量化运算.由于特征空间F的维数通常比较高,这使得计算很困难,因此需要将量化放到输入空间U进行计算,即对输入信号x(n)进行量化,那么QKLMS 算法的权值更新方程可以写为

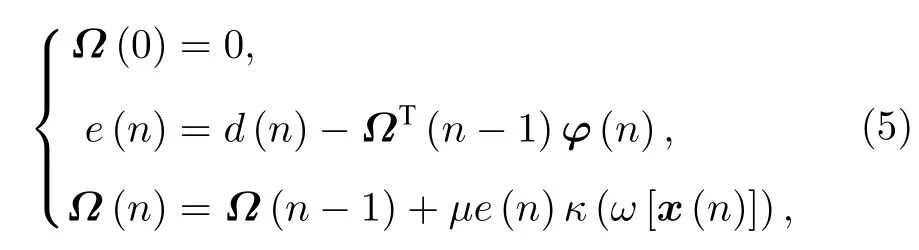
其中ω[·]是输入空间U的量化运算.为了便于后续的推导,定义φp(n)=Q[φ(n)],xp(n)=ω[x(n)].

3 量化核最小逆双曲正弦算法

3.1 核最小逆双曲正弦算法

Inverse hyperbolic sine(IHS)是双曲正弦函数的逆,其代价函数可以写成如下形式:

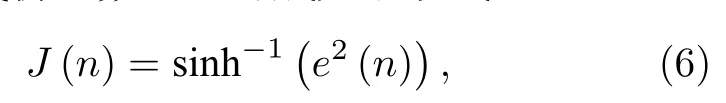
其中sinh为双曲正弦函数.利用梯度下降法,(6)式的导数形式可以写为

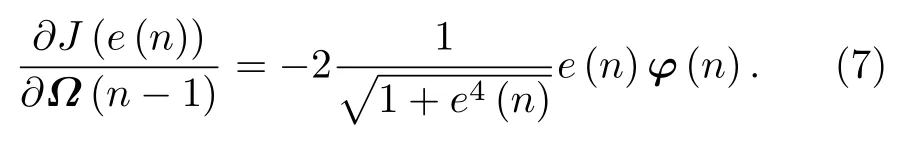
利用负随机梯度,可以推导出该KLIHS的权重更新方程为

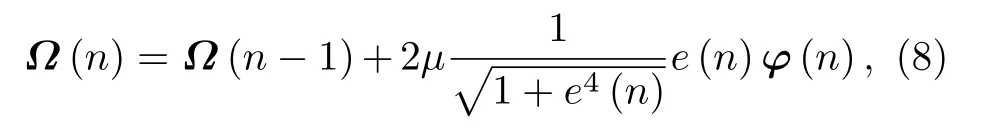
其中µ表示步长,逐项递推得到如下形式:

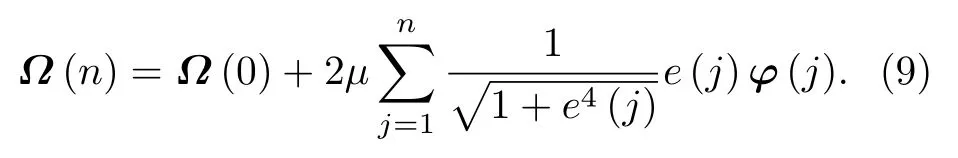
在这里Ω(0)=0,则权重更新公式为

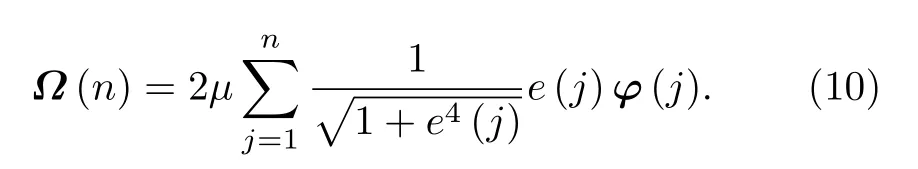
滤波器n+1 时刻的输出为

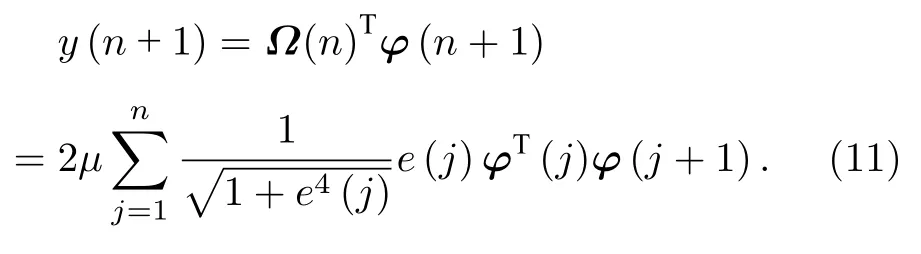
所以KLIHS 算法如表1 所列.

表1 KLIHS 算法Table 1.KLIHS algorithm.

3.2 量化核最小逆双曲正弦算法

量化核最小逆双曲正弦(QKLIHS)算法是通过量化(8)式中的φ(n)得到的,可以表示为

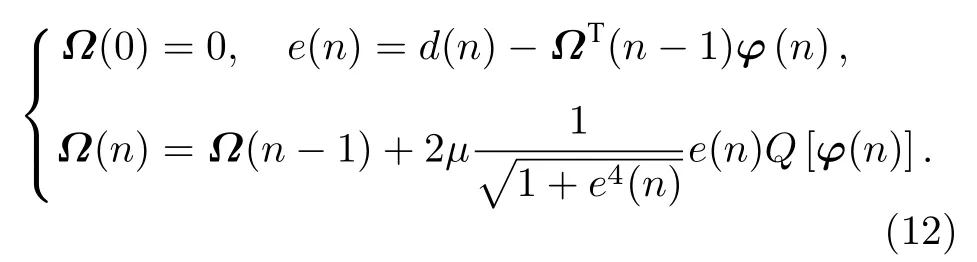
与QKLMS 类似,要把特征空间F的量化转换到输入空间U.故QKLIHS 算法的学习可以表示为

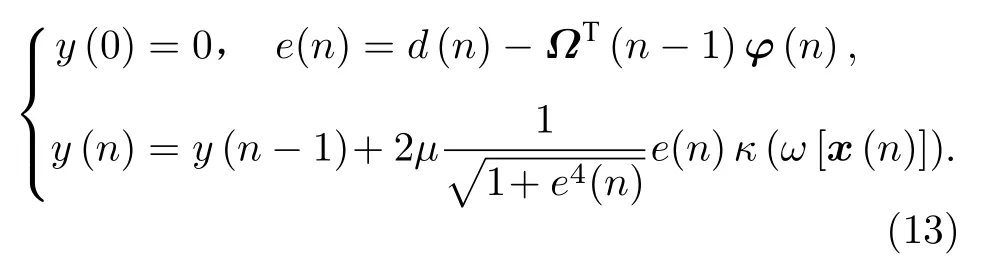
量化过程中当接收到新的输入数据x(n)时,首先需要去计算x(n)与当前字典C(n −1)的欧几里得距离,可以表示为:

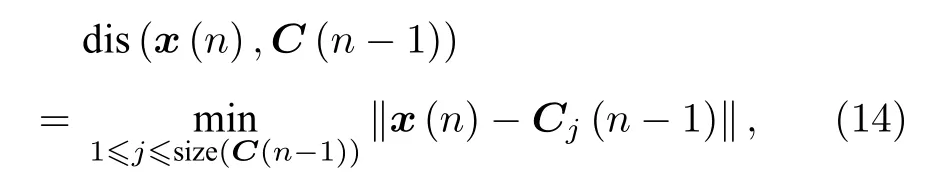
其中∥ ·∥表示范数;Cj(n −1)表示字典C(n −1)中的第j个元素.接下来就要去判断该数据是否要加入“字典”作为该字典的一个新的中心,量化阈值γ≥0用来当做判断的标准.如果dis(x(n),C(n −1))>γ,将输入数据x(n)加入到字典C(n −1)中,并加入相对应的系数向量,可以表示为

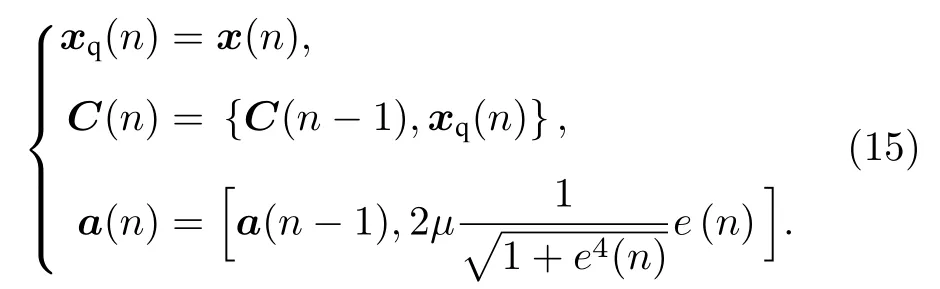
否则,即

此时输入数据x(n)不会被加入到字典C(n −1)中,但是会将字典C(n −1)中与x(n)的欧几里得距离的最近的元素Cj∗(n −1)作为x(n)的量化值,并且更新Cj∗(n −1)的系数,可以表示为

因此,获得新的样本{ x(n),d(n)}时,QKLIHS算法的输出为

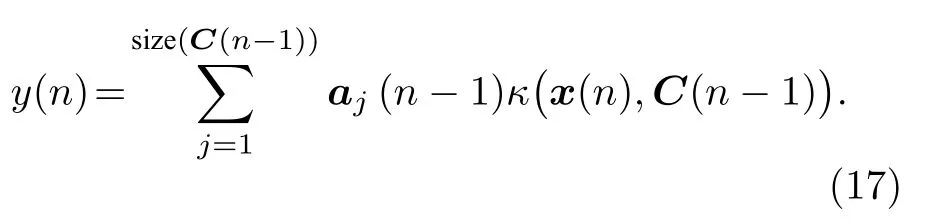
综上,QKLIHS 算法的流程如表2 所列.

表2 QKLIHS 算法Table 2.QKLIHS algorithm.

3.3 能量守恒关系

对本文提出的QKLIHS 算法的能量守恒关系进行推导.已知未知系统的输出为

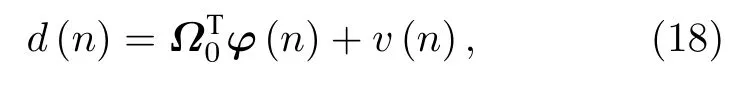
其中v(n)是噪声,输出误差为

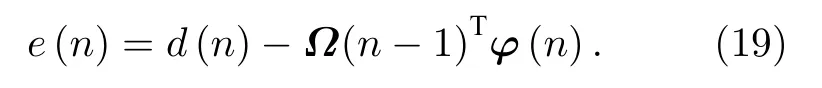
将(18)式代入(19)式得

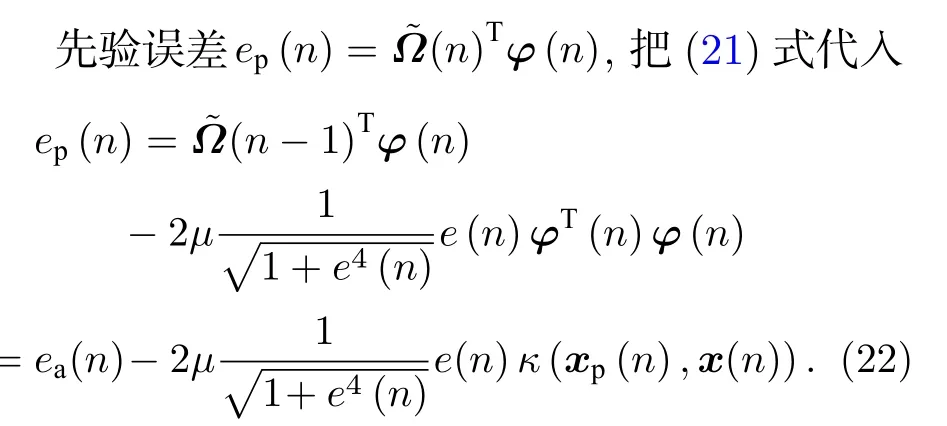
结合(21)式和(22)式消除e(n):

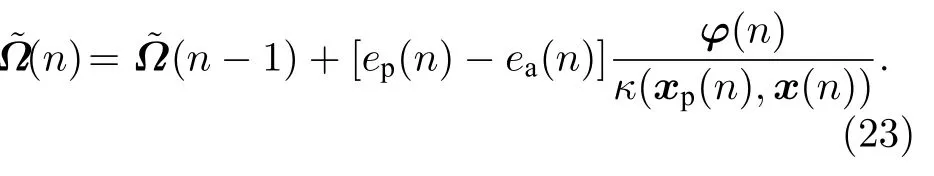
对(23)式两边取内积:

则能量守恒关系为

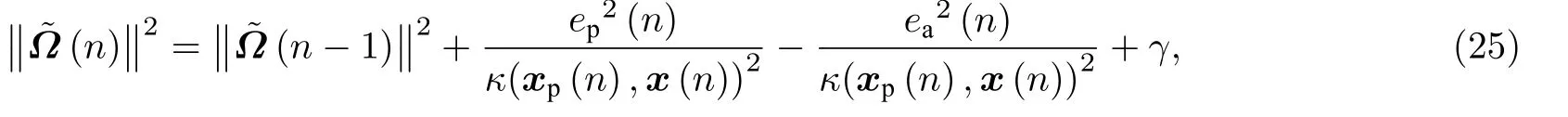
其中

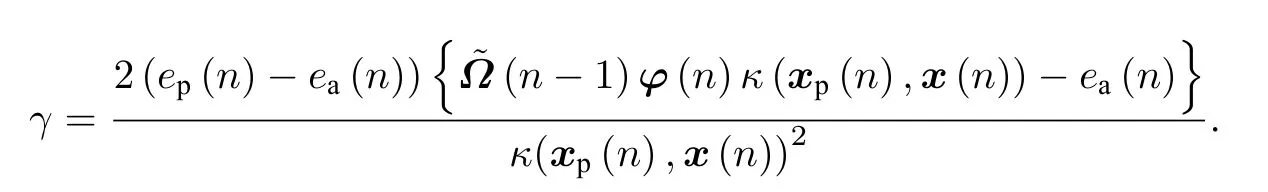
如果κ(xp(n),x(n))→1,γ →1,则能量守恒关系为

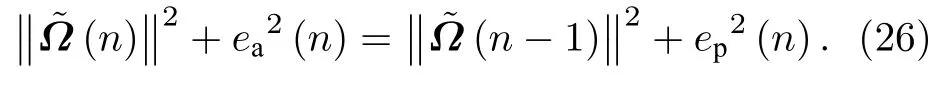
3.4 收敛性能分析

(21)式可表示为

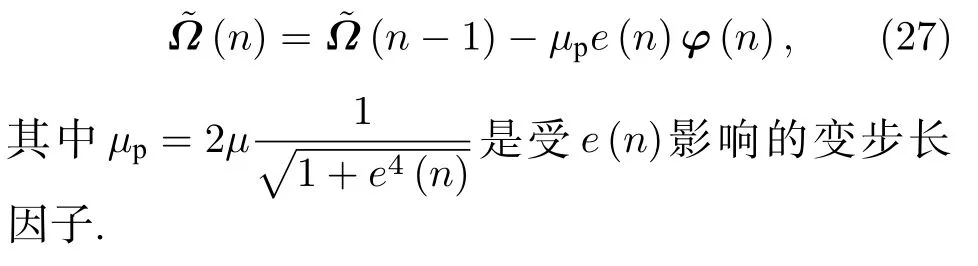
(27)式的内积为

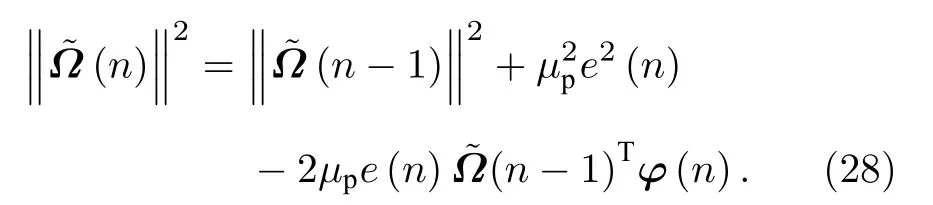
对(28)式两边取期望

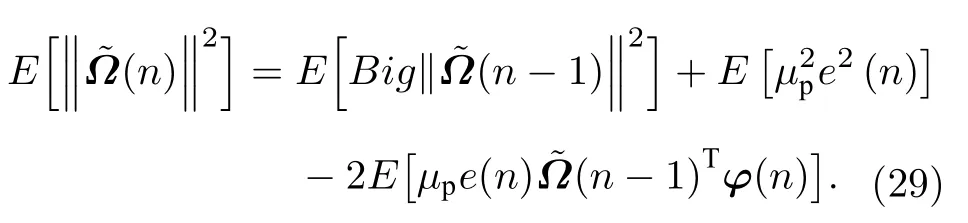
算法收敛必须满足:

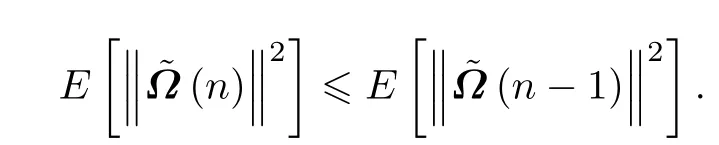
那么

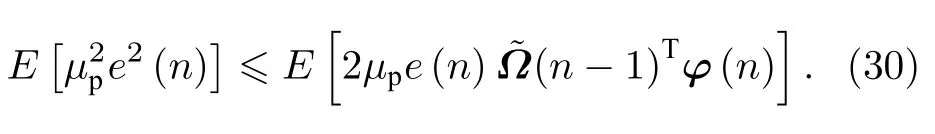
基于上述情况,步长(算法收敛的充分必要条件)满足:

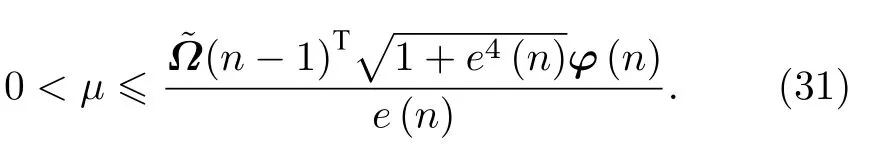
4 算法仿真

本节中给出了Mackey-Glass 短时混沌时间序列预测和非线性信道均衡两个例子来验证所提出的KLISH,QKLISH 算法的性能.对于所有的模拟,进行了200 次蒙特卡罗运行以减少干扰.所有实验高斯核核宽h=1.0,训练数据的大小为1000,测试数据的大小为100.Alpha 稳定分布模型来模拟非高斯噪声环境如图1.为了评估滤波精度,均方误差(MSE)被定义为其中S=100为测试数据的大小.

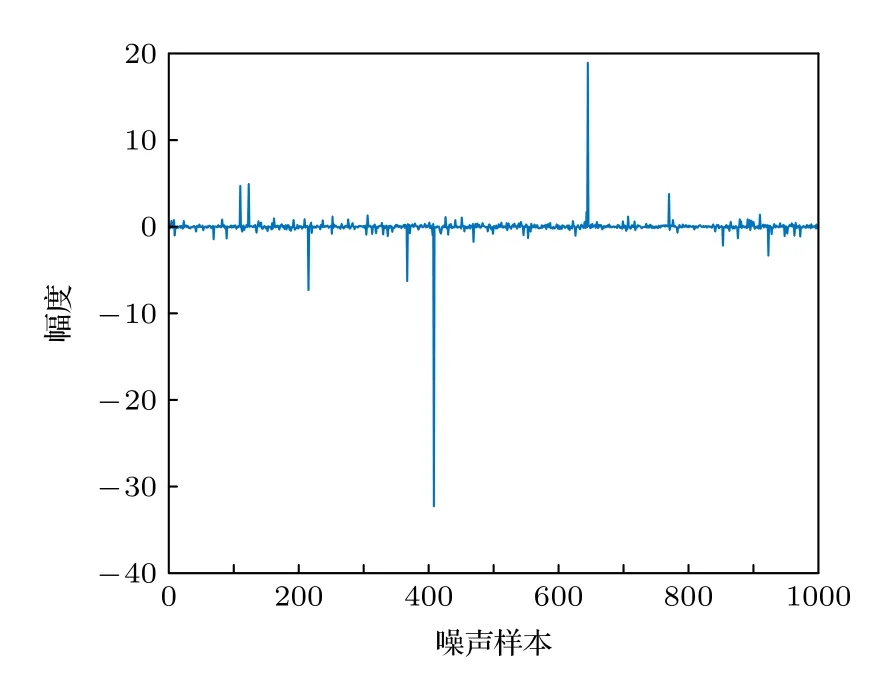
图1 α=1.3 时的Alpha 稳定分布噪声(非高斯环境)Fig.1.When α=1.3,alpha stable distribution noise(non-Gaussian environment).

4.1 短时混沌时间序列预测

Mackey-Glass 短时混沌时间序列由下列延迟微分方程生成:

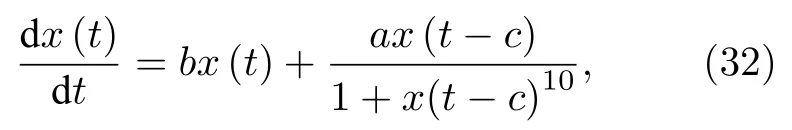
其中参数设置为:a=0.2,b=0.1,c=10.根 据Take ns 嵌入定理,用之前的7 个数据u(i)=[x(i−7),x(i −6),···,x(i −1)]T作为输入量,预测当前的输入x(i).

1)不同核自适应滤波算法对比.把本文的KLIHS算法和KLMS,KLMP,KLL,KMCC 算法性能进行对比,结果如图2 所示.表3 给出了各算法达到稳态时候的稳态误差的均值和标准偏差.

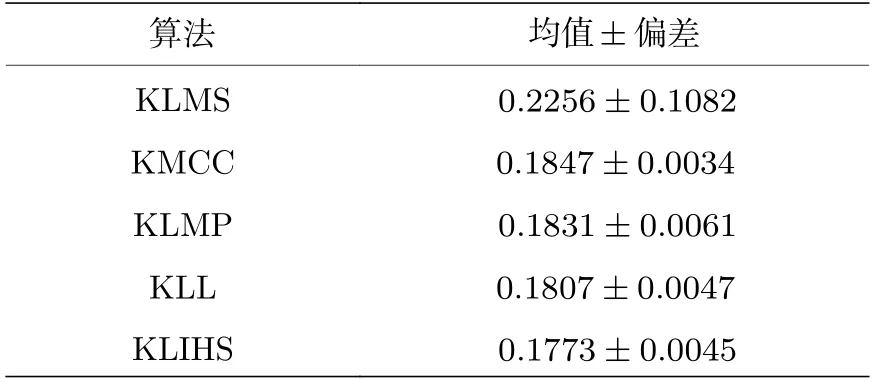
表3 在短时混沌时间序列预测下不同算法的均值±标准偏差Table 3.The mean standard deviation of different algorithms under short-term chaotic time series prediction.

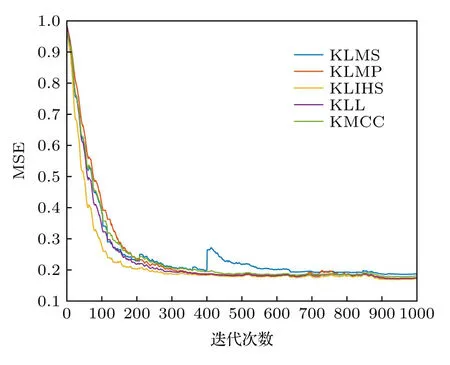
图2 在短时混沌时间序列预测下不同算法的性能比较Fig.2.Performance comparison of different algorithms under short-time chaotic time series prediction.

从图2和表3 可以看出,在非高斯噪声环境下KLMS 算法不具有鲁棒性,而本文算法和KLMP,KLL,KMCC 算法都具有鲁棒性,并且都能达到比较好的稳态误差,同时本文算法的收敛速度比其他几种算法都要快.由此可得本文所提的KLIHS 算法在短时混沌时间序列预测环境下性能较好.

2)讨论量化阈值γ取不同值时对算法性能的影响.文中γ分别取0,0.5,0.9,1.2和2.0,QKLIHS算法的学习曲线和网络尺寸大小分别如图3和图4所示.从图3和图4中可以看出,当量化阈值γ为0时,QKLIHS 算法的网络尺寸和迭代次数成正比,此时的QKLIHS 算法退化为KLIHS 算法.随着γ的增大,网络尺寸减小,该算法性能也随之下降.为了更清晰地分析不同量化阈值对算法性能的影响,表4 给出了在短时混沌时间序列预测环境下,不同量化阈值的QKLIHS 算法达到稳态时的均方误差和网络尺寸.由表4 分析可知,量化阈值从0 变化到1.2,QKLIHS 算法的均方误差增大了不到0.01,但该算法的网络尺寸却从1000 变到101,降低了10 倍.当γ≤1.2时,在保证基本不损失稳态误差性能的基础下,最大程度地降低算法的计算复杂度.

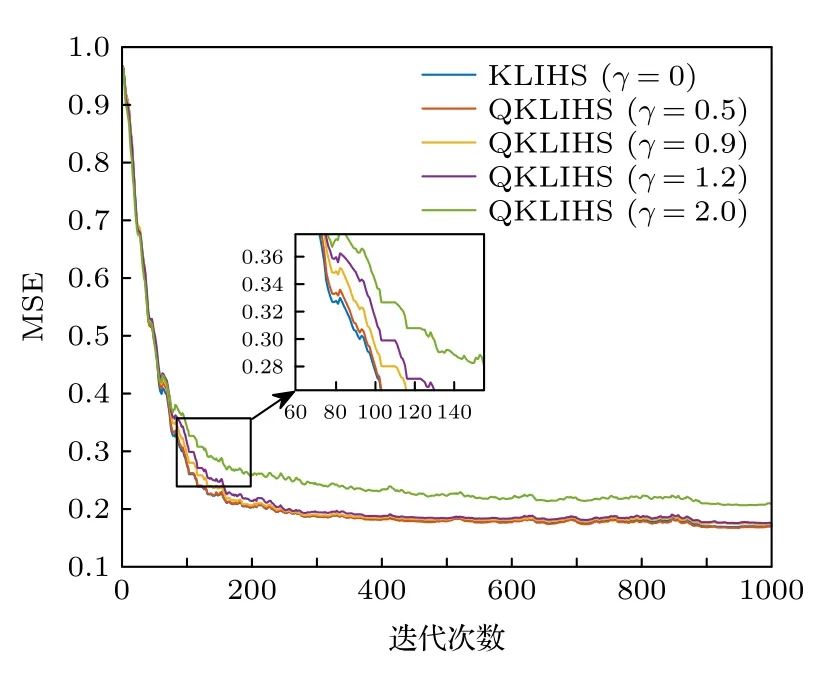
图3 在短时混沌时 间序列预测下 不同量化阈值 γ的QKLIHS 算法的性能比较Fig.3.Performance comparison of QKLIHS algorithms with different quantization thresholds γ under short-time chaotic time series prediction.

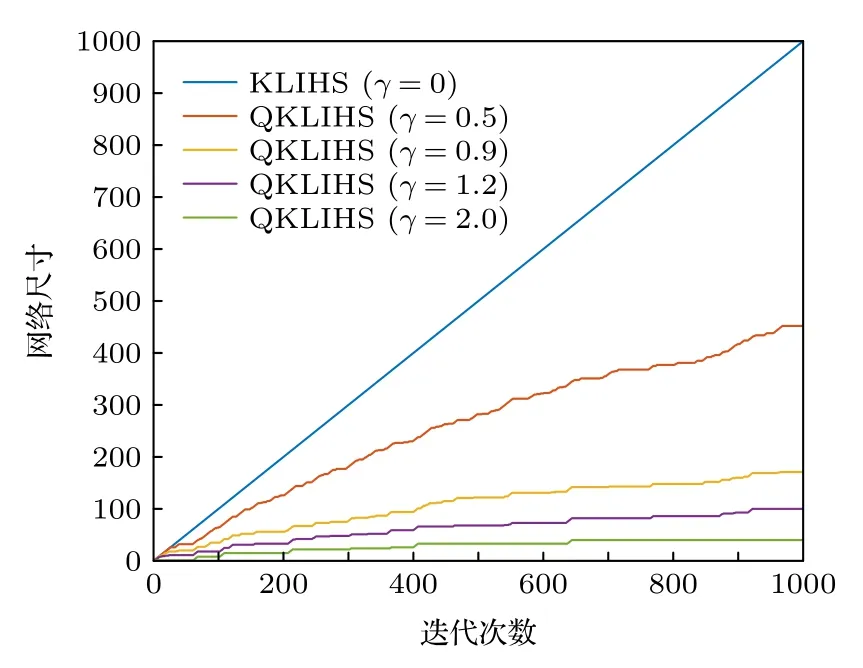
图4 在短时混沌时间序列预测下不同量化阈值 γ的QKLIHS算法的网络尺寸比较Fig.4.Network size comparison of QKLIHS algorithms with different quantization thresholds γ under short-time chaotic time series prediction.

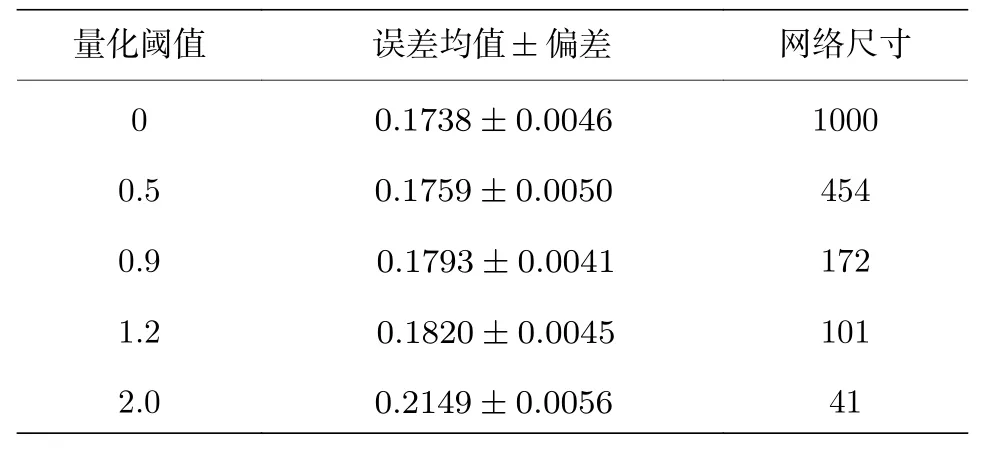
表4 在短时混沌时间序列预测下不同量化阈值的QKLI HS 算法的均方误差与网络尺寸比较Table 4.Comparison of mean square error and network size of QKLIHS algorithm with different quantization thresholds γ under short-time chaotic time series prediction.

4.2 非线性信道均衡

非线性信道模型由线性滤波器和无记忆非线性模型组成.图5为一个非线性信道的方框图,其中u(n)∈{−1,1}为信道输入,x(n)=u(n)+0.5u(n −1)为线性滤波器的输出,r(n)=x(n)−0.9x(n)2+v(n)为非线性信道的输出,其中v(n)为噪声.信道均衡的目标是构造一个逆滤波器以尽可能低的错误率恢复原始信号.可以将其看做一个简单的回归问题,其样本为{([r(n),r(n+1),···,r(n+l),u(n −D)])},l是时间嵌入长度,D是均衡滞后时间.实验中,l=3,D=2.

图5 非线性信道Fig.5.Nonlinear channel.

1)不同核自适应滤波算法对比.上述五种不同算法的学习曲线如图6 所示.从图6 可以看出,本文的算法和其他的四种算法能达到相同的稳态误差,并且都有较好的鲁棒性,但是本文算法的收敛速度优于其他四种算法.综上所述,本文所提出的算法在非线性信道均衡环境下性能较好.

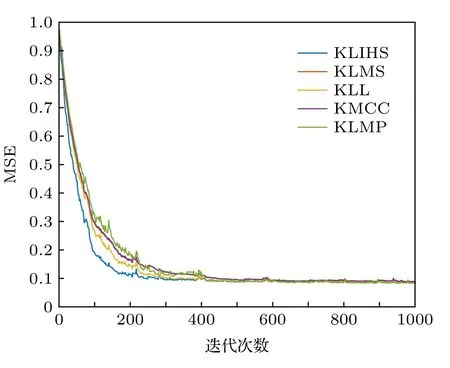
图6 在非线性信道均衡下不同算法的性能比较Fig.6.Performance comparison of different algorithms under nonlinear channel equalization.

2)讨论量化阈值γ取不同值时对算法性能的影响.文中γ分别取0,0.5,0.9,1.2和2.0,不同量化阈值的QKLIHS 算法的学习曲线和网络尺寸大小分别如图7和图8 所示.从图7和图8 中可以看出,当量化阈值γ=0时,QKLIHS 算法退化为KLIHS算法,此时网络尺寸和迭代次数成正比.当γ逐渐增大,网络尺寸减小,算法性能下降.为了更清晰地看出稳态误差的差距,给出了在当前仿真下的均方误差和网络尺寸,如表5 所列.分析表5 可以得到,在γ≤1.2时,网络尺寸的减小的程度远远大于稳态误差增加的程度.因此,QKLIHS 算法可以在保证基本不损失稳态误差性能的基础下,能最大程度地降低算法的计算复杂度.

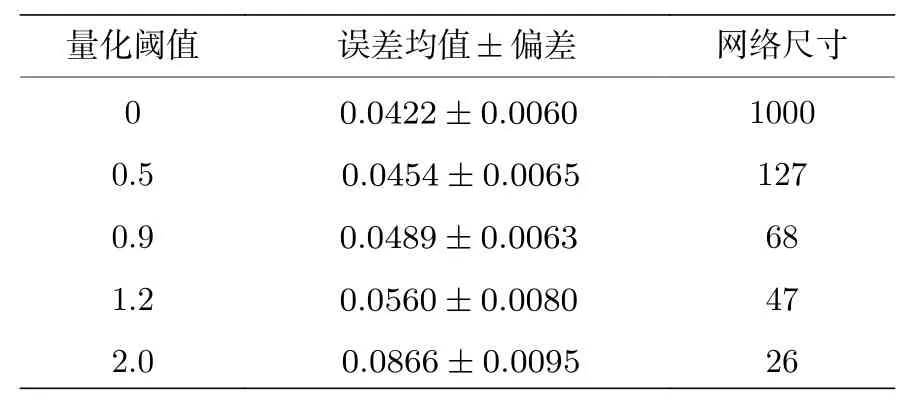
表5 在非线性信道均衡下不同量化阈值 γ的QKLIHS算法的稳态误差均值与网络尺寸Table 5.Steady-state error mean and network size of QKLIHS algorithm with different quantization threshold γ under nonlinear channel equalization.

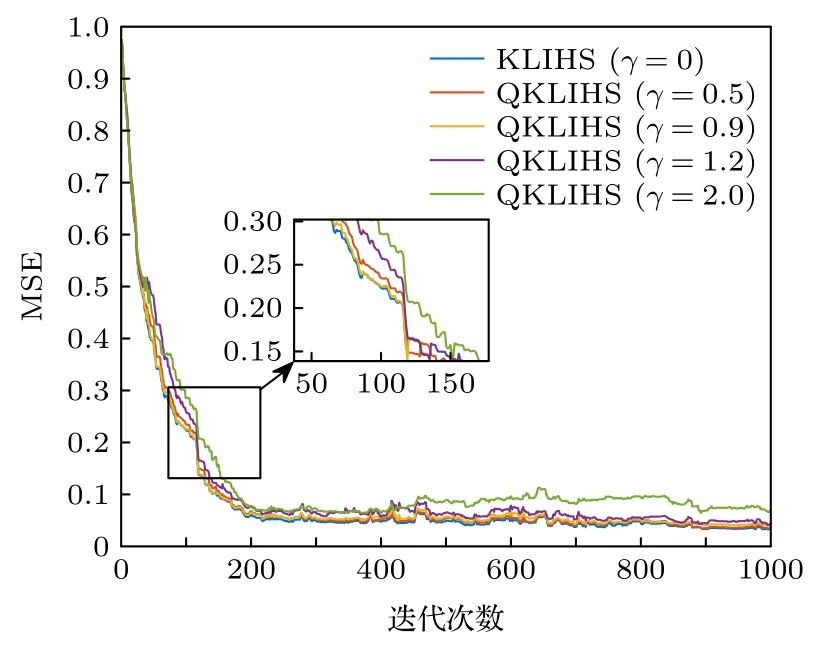
图7 在非线性信道 均衡下不同量化阈值 γ的QKLIHS算法的性能比较Fig.7.Performance comparison of QKLIHS algorithms with different quantization thresholds γ under nonlinear channel equalization.

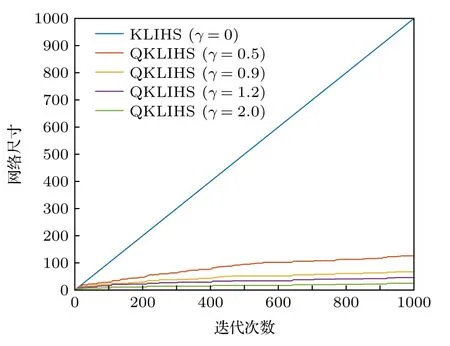
图8 在非线性信道 均衡下不同量化阈值 γ的QKLIHS算法的网络尺寸比较Fig.8.Network size comparison of QKLIHS algorithms with different quantization thresholds γ under nonlinear channel equalization.

5 结论

将核方法和双曲正弦函数的逆相结合,提出了一种适用于非高斯环境的鲁棒核最小逆双曲正弦算法.同时考虑到该算法网络尺寸线性增长的问题,进一步利用向量量化方法,推导出了能够抑制网络规模增长的量化核最小逆双曲正弦算法,给出了该算法的能量守恒关系和收敛条件.仿真结果表明,提出的核最小逆双曲正弦算法的性能优于KLMS,KLMP,KMCC和KLL 算法,且量化核最小逆双曲正弦算法在保证滤波精度的前提下,能够有效地减少网络尺寸,降低了算法的计算复杂度.