边容错3元n立方体的两条等长不交覆盖路

佘卫强

（漳州职业技术学院通识教育学院,福建漳州 363000）

在并行算法处理和并行计算系统中，超立方体有许多优良性质，使得它成为当今最有效，最常用的网络拓扑结构.1977 年第一台超立方体并行处理机问世，随后互连网飞跃发展，网络系统越来越复杂，同时计算机元件或线路故障也频繁发生，使得人们更注重网络的稳定性和实效性，大家也意识到了超立方体自身存在的固有缺点，因此超立方体的许多变形网络也这样被提出来，目的都是为了改进超立方体的不足，其中最具代表性的变形网络拓扑结构有k元n立方体，它能实现很多算法从而提供更有效的通信模式，因而k元n立方体的并行算法，路由选择，连通度，容错性和嵌入路（圈）多路等问题就成为了许多学者关注的研究点,见文献[1-5].在实时系统网络中，多条点不交路可以提高网络传输的实效性和稳定性，近年来，学者在一对多条不交路和多对多条不交路覆盖的方向上研究已经获得了许多有价值的成就（见文献[6-13]），但学者对这些路径是否等长度方面得到成果比较少.讨论在边容错条件下3元n立方体中两条等长顶点不交覆盖路嵌入.将证明下面结论.

定理1当n≥2,边故障集|F|≤n-2 时，在中任意三个顶点x,y1,y2,则在-F中存在两条内部顶点不交的等长覆盖路P1=(x,···,y1)和P2=(x,···,y2).

1 预备知识和引理

文中的概念和记号参见文献[14]，E(G)和V(G)分别代表图G的边集和顶点集.P=v0e1v1e2v2…ekvk表示以v0为起点和以vk为终点的路；路P=v0e1v1e2v2…ekvk包含k条边，称路P的长度|P|为k；如果两条路P1和P2各自包含的边数个数相等，则称路P1和P2等长，记为|P1|=|P2|.对于故障集F⊂V(G)∪E(G)且|F|≤k,在G-F中任取两个端点x和y，若在G-F中有一条连接x和Qn-F的哈密尔顿路，则称图G是k边(点)容错哈密尔顿可迹.给定图G中m个源点s1,s2,…,sm和m个汇点t1,t2,…,tm，若图有m条内部点不交路P1,P2,…,Pm覆盖图G的所有顶点，这里Pi=(si,···,ti)，i∈{1,2,…,m}，即V(Pi)∩V(Pj)=∅，V(Pi)∪V(Pj)=V(G)，i,j∈{1,2,…,m}，则称图G是m条点不交覆盖路的，若这m条不交路P1,P2,…,Pm长度都是相等的，则称G为m条等长不交覆盖路的.

2 定理1的证明

证明下面采用归纳法对n作归纳证明.

情况1若x,y1,y2在Q[0]中.

当F0≤n-2，取(w,h)∈F0，在归纳假设得，在Q[0]-F0+(w,h)中存在两条内部顶点不交的等长覆盖路l1=(x,···,y1)和l2=(x,···,y2).若(w,h)∈l1或(w,h)∈l2，则不妨假设(w,h)∈l1，则在路l1上取边(w,h)，重新记边(w,h)=(u,v)，若(w,h)∉l1且(w,h)∉l2，则在路l1上取一条边(u,v)，(u1,v1)是(u,v)在Q[1]的对应边，由引理1得，在Q[1]-F1中存在一条哈密尔顿路l3=(u1,···,v1).在路l2上取一条边(s,t)，(s2,t2)是(s,t)在Q[2]的对应边，由引理1得，在Q[2]-F2中存在一条哈密尔顿路l4=(s2,···,t2).令P1=(l1-(u,v))∪(u,u1)∪(v,v1)∪l3，P2=(l2-(s,t))∪(s,s2)∪(t,t2)∪l4,又|P1|=|P2|且V(P1)∪V(P2)=，这里P1连接x和y1，P2连接x和y2.则上述两条等长不交路P1和P2满足定理1要求，如图1所示.

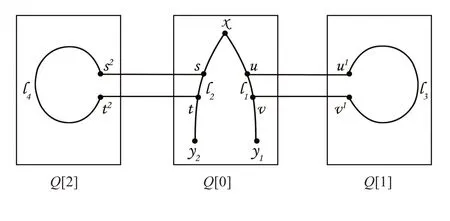
图1 x,y1,y2在Q[0]中的情况Fig.1 x,y1,y2 in Q[0]

情况2若x,y1在Q[0]中，y2在Q[1]中.

当F0≤n-3.由于3n-1＞3，故在Q[0]中存在一点w，使得w≠x≠y1且w在Q[1]的对应点w1≠y2，在归纳假设得，在Q[0]-F0中存在两条内部顶点不交的等长覆盖路l1=(x,···,y1)和l2=(x,···,w).在路l1上取一条边(s,t)，(s2,t2)是(s,t)在Q[2]的对应边，由引理1 得，在Q[2]-F2中有一条哈密尔顿路l3=(s2,···,t2)，由引理1 得，在Q[1]-F1中存在一条哈密尔顿路l4=(w1,···,y2).令P1=(l1-(s,t))∪(s,s2)∪(t,t2)∪l3，P2=l2∪(w,w1)∪l4,又V(P1)∪V(P2)=且|P1|=|P2|，这里P1连接x和y1，P2连接x和y2.则上述两条等长不交路P1和P2满足定理1要求，如图2所示.

图2 F0≤n-3的情况Fig.2 The case if F0≤n-3

当F0=n-2.由引理1得，在Q[0]-F0中有一条哈密尔顿路l1连接x和y1，在路l1上存在一条边(s,t)将路l1分成l2=(x,···,s)和l3=(t,···,y1)，使得|l2|=(3n-1-1)/2和|l3|=(3n-1-1)/2-1.设x和t在Q[2]的对应点分别为x2和t2，由引理1得，在Q[2]中存在一条哈密尔顿路l4=(x2,···,t2).若s在Q[1]的对应点s1≠y2，由引理1得，在Q[1]中存在一条哈密尔顿路l5=(s1,···,y2)，令P1=(x,x2)∪l4∪(t2,t)∪l3，P2=l2∪(s,s1)∪l5,又V(P1)∪V(P2)=且|P1|=|P2|，这里P1=(x,···,y1)，P2=(x,···,y2).则上述两条等长不交路P1和P2满足定理1要求，如图3所示.若s在Q[1]的对应点s1=y2，在l2上取一条边(u,v)，设(u1,v1)是(u,v)在Q[1]的对应边，由引理1得，在Q[1]-y2中存在哈密尔顿路l6=(u1,···,v1).令P2=(l2-(u,v))∪(u,u1)∪l6∪(v,v1)∪(s1,y2)，P1=(x,x2)∪l4∪(t2,t)∪l3.则上述两条等长不交路P1和P2满足定理1，如图4所示.

图3 F0=n-2,s1≠y2 的情况Fig.3 The case of F0=n-2,s1≠y2

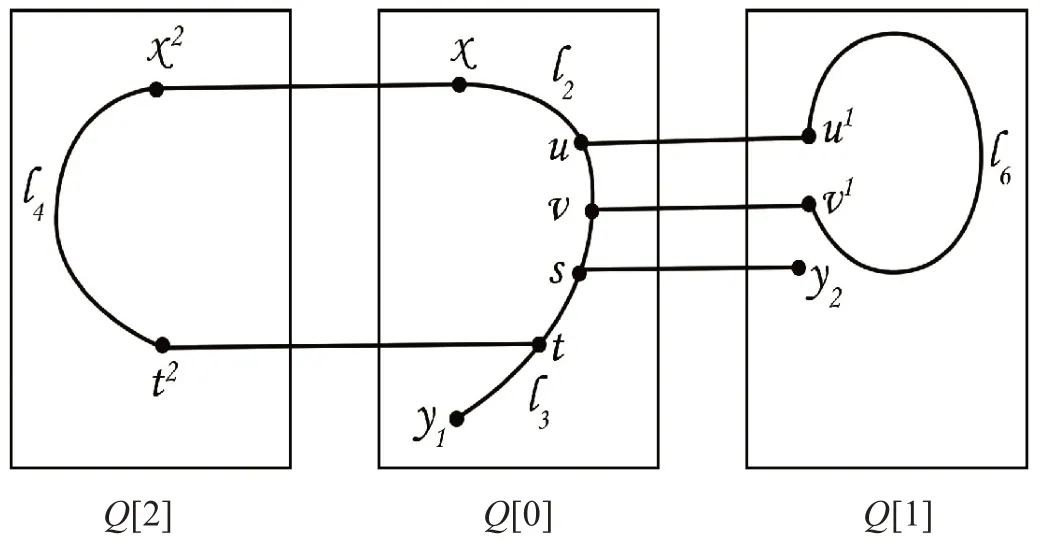
图4 F0=n-2,s1=y2的情况Fig.4 The case of F0=n-2,s1=y2

情况3若x在Q[0]中，y1，y2在Q[1]中.

当1 ≤F0≤n-2.因为F1≤n-3，在Q[1]中取一点s，使得s≠y1≠y2且s在Q[0]的对应点s0≠x，在归纳假设得，在Q[1]-F1中存在两条内部顶点不交的等长覆盖路l1=(s,w,···,y1)和l2=(s,h,···,y2)，由引理1 得，在Q[0]-F0中存在一条哈密尔顿路l3=(x,···,s0).设x在Q[2]的对应点x2，设w和h在Q[2]的对应点分别为w2和h2，则有w2≠x2或h2≠x2，不妨设h2≠x2，由引理1得，在Q[2]-F2中存在一条哈密尔顿路l4=(h2,···,x2).令P1=l3+(s0,s)∪l1，P2=(x,x2)∪l4∪(h2,h)∪(l2-(s,h)),又|P1|=|P2|，则上述两条等长不交路P1和P2满足定理1要求，如图5所示.

图5 1≤F0≤n-2的情况Fig.5 The case of 1 ≤F0≤n-2

当F0=0.因为F1≤n-2，由引理1得，在Q[1]-F1中存在一条哈密尔顿路l1连接y1和y2.在路l1上存在一条边(s,t)将路l1分成l2=(y1,···,s)和l3=(t,···,y2)，使得|l2|=a和|l3|=3n-1-1-a，这里1≤a≤3n-1-2.设(s,t)在Q[2]的对应边为(s2,t2)，因为F2≤n-2，由引理1 得，在Q[2]-F2中有哈密尔顿路l4=(s2,···,t2).在路l4上存在一条边(u,v)将路l4分成l5=(s2,···,u)和l6=(t2,···,v)，使得|l5|=3n-1-1-a和|l6|=a，这里1 ≤a≤3n-1-2.因a的取值有3n-1-2 种，所以必定存在u0≠v0≠x，这里(u0,v0)是(u,v)在Q[0]的对应边，由归纳假设得，在Q[0]中存在两条点不交的等长覆盖路l7=(x,···,u0) 和l8=(x,···,v0).令P1=l7∪(u0,u)∪l5∪(s2,s)∪l2，P2=l8∪(v0,v)∪l6∪(t2,t)∪l3,又|P1|=|P2|，则上述两条等长不交路P1和P2满足定理1要求，如图6所示.

图6 F0=0的情况Fig.6 The case of F0=0

情况4若x在Q[0]中，y1在Q[1]中，y2在Q[2]中.

当F0≤n-2.由引理2，在Q[0]-F0中存在一条哈密尔顿圈C=(x,···,s,t,···,x)，因为|C|=3n-1是奇数，所以圈C中存在一条边(s,t)使得(x,···,s)=l1和(x,···,t)=l2长度相等，假设s在Q[1]的对应点s1，t在Q[2]的对应点t2，若s1≠y1且t2≠y2，由引理1得，在Q[1]-F1中存在一条哈密尔顿路l3=(s1,···,y1).由引理1得，在Q[2]-F2中存在一条哈密尔顿路l4=(t2,···,y2).令P1=l1∪(s,s1)∪l3，P2=l2∪(t,t2)∪l4,又|P1|=|P2|且V(P1)∪V(P2)=，这里P1连接x和y1，P2连接x和y2.则上述两条等长不交路P1和P2满足定理1要求.若s1≠y1且t2=y2（或s1=y1且t2≠y2），不妨设s1≠y1且t2=y2，由引理1 得，在Q[1]-F1中存在一条哈密尔顿路l5=(s1,···,y1).在路l2中取一条边(u,v)，使得u2≠v2≠y2，这里(u2,v2)是(u,v)在Q[2]的对应边，由引理1得，在Q[2]-F2-y2中存在一条哈密尔顿路l6=(u2,···,v2).则如图7 所示上述两条等长不交路P1和P2满足定理1要求.若s1=y1且t2=y2，在路l1中取一条边(w,h)，使得w1≠h1≠y1，这里(w1,h1)是(w,h)在Q[1]的对应边，由引理1 得，在Q[1]-F1-y1中存在一条哈密尔顿路l7=(w1,···,h1).在路l2中取一条边(u,v)，使得u2≠v2≠y2，这里(u2,v2)是(u,v)在Q[2]的对应边，由引理1 得，在Q[2]-F2-y2中存在一条哈密尔顿路l8=(u2,···,v2).则如图8所示上述两条等长不交路P1和P2满足定理1要求.

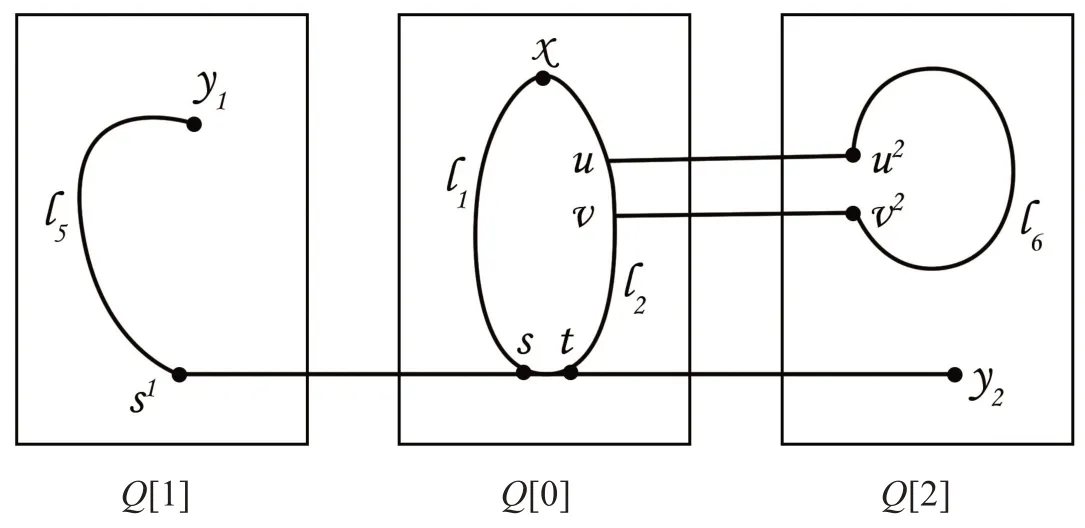
图7 s1≠y1且t2=y2的情况Fig.7 The case of s1≠y1 and t2=y2

图8 情况4 s1=y1且t2=y2Fig.8 The case of s1=y1 and t2=y2

证毕.

3 展望

文中研究了边故障3 元n立方体中存在两条等长覆盖路问题，定理1 故障边数|F|≤n-2 是否已经达到最佳上界?网络系统中结点故障的出现必然影响系统的直径，若3 元n立方体中故障出现在结点时，在3元n立方体中删除故障结点后是否依然存在两条等长覆盖路等问题都值得后续加以研究.