STRONG LIMIT THEOREMS FOR EXTENDEDINDEPENDENT RANDOM VARIABLES ANDEXTENDED NEGATIVELY DEPENDENT RANDOMVARIABLES UNDER SUB-LINEAR EXPECTATIONS*

Li-Xin ZHANG(张立新)

School of Mathematical Sciences，Zhejiang Universitg，Hangzhou 310027，China E-mail : stazlax@zju.edu.cn

for all n ≥2 and any ψ ∈Cl,Lip(Rn+1), where Cl,Lip(Rn+1)is the space of local Lipschitz functions in Rn+1. Under Peng’s framework, many limit theorems have been recently established,including the central limit theorem and the weak law of large numbers (c.f. Peng [20, 22]),the law of the iterated algorithm (c.f. Chen and Hu [3], Zhang [31]), the small derivation and Chung’s law of the iterated logarithm (c.f. Zhang [29]), and the moment inequalities for the maximum partial sums(c.f. Zhang[30]). Zhang[30]gave the sufficient and necessary condition for the Kolomogov strong law of large numbers.

Recall that two random variables, X and Y, are independent relative to a probability P if and only if, for any Borel functions f and g, EP[f(X)g(Y)] = EP[f(X)]EP[g(Y)] whenever the expectations considered are finite. Another possible way to define the independence of{Xn;n ≥1} is that

where P is a family of probability measures defined on a measurable space (Ω,F). The strong law of large numbers was proven under finite (1 + α)-th moments (α > 0). Note that if{Xn;n ≥1} are independent relative to each P ∈P, then we will have

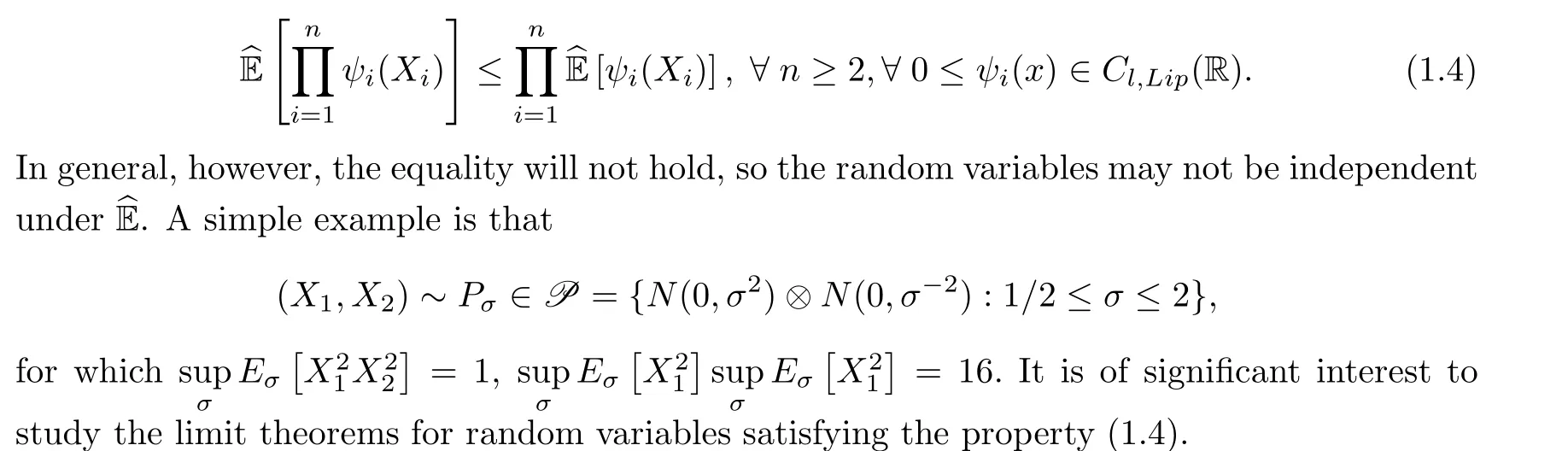
The property (1.4) is very close to that of negatively dependent random variables. The concept of negative dependence relative to the classical probability has been extensively investigated since it first appeared in Lehmann[9]. Various generalization of the concept of negative dependence and the related limit theorems have been studied; one can refer to Joag-Dev and Proschan [8], Newman [15], Matula [13], Su, Zhao and Wang [25], Shao and Su [24], Shao[23], Zhang [27, 28] etc.. As an extension of negative dependence, the concept of extended negative dependence was proposed in Liu [10] and further promoted in Chen, Chen and Ng[1]. A sequence of random variables is said to be extended negatively dependent if the tails of their finite-dimensional distributions in the lower-left and upper-right corners are dominated by a multiple of the tails of the corresponding finite-dimensional distributions of a sequence of independent random variables with the same marginal distributions. The strong law of large numbers was established by Chen, Chen and Ng [1]. However, for the extended negatively dependent random variables, besides the law of large numbers, very little is known about fine limit theorems such as the central limit theorem and the law of the iterated logarithm. In this paper, we will introduce a concept of extended negative dependence under the sub-linear expectation which is weaker than the extended independence as defined in (1.3), and which is an extension of the extended negative dependence relative to the classical probability. The strong law of large numbers and the law of the iterated logarithm will be established for extended negatively dependent random variables. As a corollary, the result of Chen, Chen and Ng [1] is extended and improved. We will show that, for a sequence of extended negatively dependent and identically distributed random variables{Xn;n ≥1}in a sub-linear expectation space, the sufficient condition for the strong law of large numbers to hold is that the Choquet integral of|X1| is finite, i.e.,

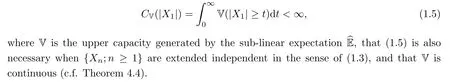
To establish the strong law of large numbers, some key inequalities for the tails of the capacities of the sums of extended negatively dependent random variables in the general sublinear expectation spaces are obtained, including the moment inequalities and the Kolmogorov type exponential inequalities. These inequalities also improve upon those established by Chen,Chen and Ng [1] for extended negatively dependent random variables relative to a classical probability,as well as those for independent random variables in a sub-linear expectation space.They may be useful tools for studying other limit theorems. The law of the iterated logarithm is also established by applying the exponential inequalities. As a corollary, the law of the iterated logarithm for extended negatively dependent random variables on a probability space is obtained. In the next section, we give some notations under the sub-linear expectations. In Section 3, we will establish the exponential inequalities. The law of large numbers is given in Section 4. In the last section, we consider the law of the iterated logarithm.

2 Basic Settings

We use the framework and notations of Peng [20]. Let (Ω,F) be a given measurable space and let H be a linear space of real functions defined on (Ω,F) such that if X1,...,Xn∈H,then φ(X1,...,Xn)∈H for each φ ∈Cl,Lip(Rn), where Cl,Lip(Rn) denotes the linear space of(local Lipschitz) functions φ satisfying

They are called extended negatively dependent (END) if they are both LEND and UEND (c.f.Liu [10]). In the case K = 1, the notion of END random variables reduces to the well known notion of the so-called negatively dependent (ND) random variables which was introduced by Lehmann [9] (c.f. also Block, Savits and Shaked [5], Joag-Dev and Proschan [8] etc.). It is shown that if {Yn;n ≥1} are upper (resp. lower) extended negatively dependent, and the functions gi≥0, i=1,2,..., are all non-decreasing (resp. all non-increasing), then

whenever the non-negative functions gi∈Cb,Lip(R), i = 1,2,... are all non-decreasing (resp.all non-increasing). They are called extended negatively dependent if they are both upper extended negatively dependent and lower extended negatively dependent.

3 Exponential Inequalities

The remainder of the proof is similar to that of Zhang [31], but for the completeness of this paper, we also present it here.

Then, setting r = p > p/2, multiplying both sides of (3.3) by pxp-1, and integrating on the positive half-line, we conclude (3.4). □

4 The Law of Large Numbers

However, we have no inequality to estimate the lower capacity V(·) such that (4.7) can be verified. We shall now introduce a more technical method to show (4.6). Let g∊be a nondecreasing function satisfying that its derivatives of each order are bounded, that g∊(x) = 1 if x ≥1, that g∊(x)=0 if x ≤1-∊, and that 0 ≤g∊(x)≤1 for all x, where 0 ＜∊＜1. Then

Then it can be shown that V∗(A) is a countably sub-additive capacity with V∗(A)≤V(A) and the following properties:

Remark 4.8 In Theorem 4.4 (c), Corollary 4.5 and Theorem 4.6, the continuity of the capacity V is assumed. This is a stringent condition. We do not know whether or not this assumption can be weakened.

For proving the theorems, we need the following lemma, which can be found in Zhang[30]:

Lemma 4.9 Suppose that X ∈H and CV(|X|)＜∞.

(4.9) is proven.

Finally, if {Xn;n ≥1} are lower extended negatively dependent, then {-Xn;n ≥1} are upper extended negatively dependent, so

The proof of (4.10) is now complete.

5 The Law of the Iterated Logarithm

If X1,X2,... are extended negatively dependent, then

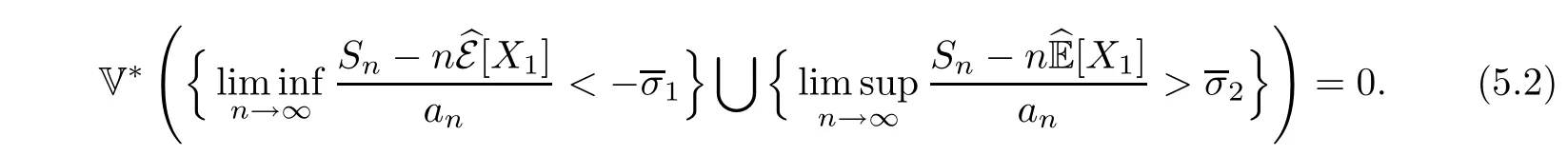
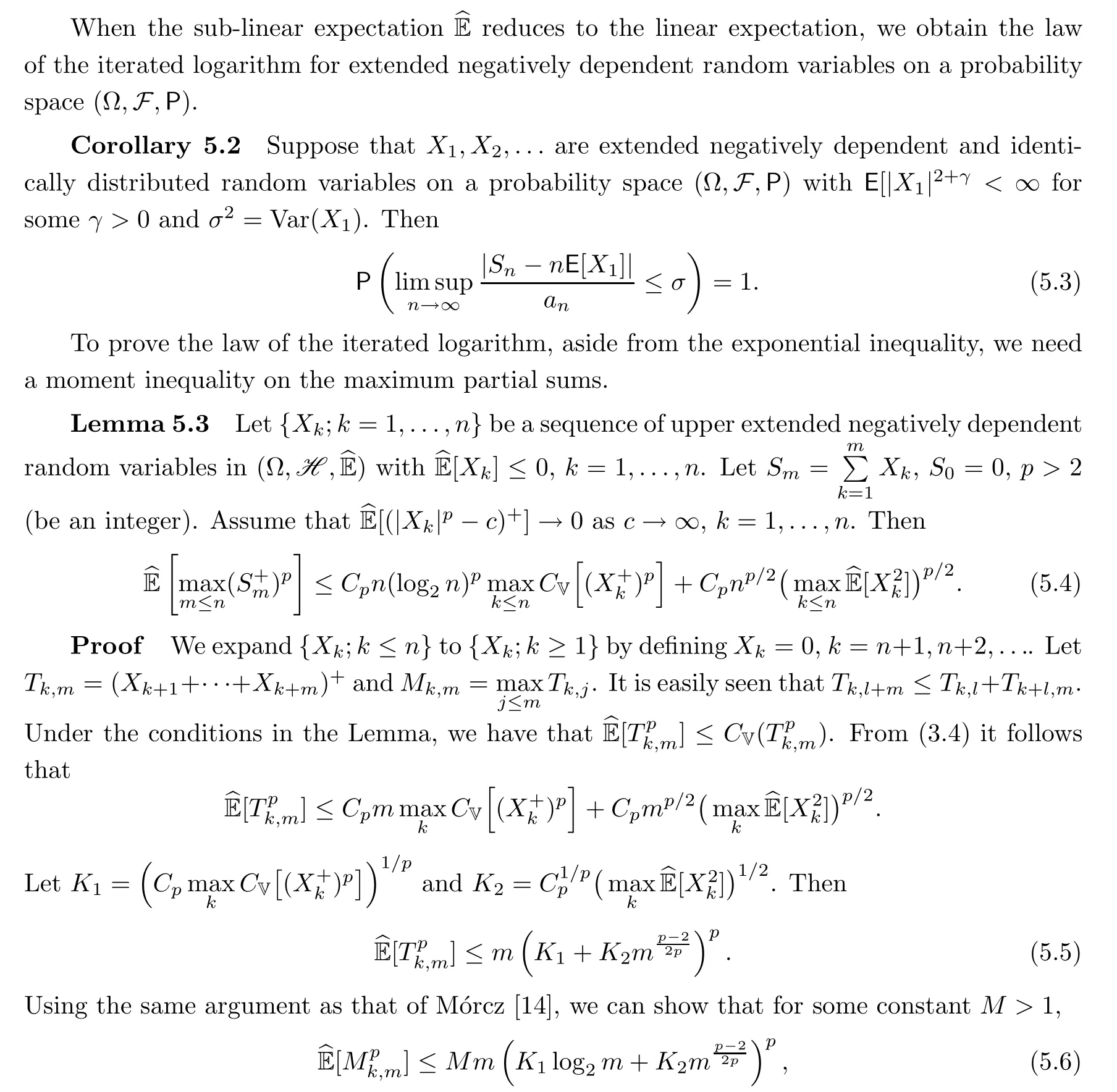
which implies (5.4). Here we only give the proof for integer p because it is sufficient for our purposes. Also, it is sufficient to show that (5.6) holds for any m = 2I. Suppose that (5.6)holds for m = 2I. We will show, by induction, that this is also true for m = 2I+1. Now, if i ≤2I, then Tk,i≤Mk,2I. If 2I+1 ≤i ≤2I+1, then Tk,i≤Tk,2I+Mk+2I,2I, and so

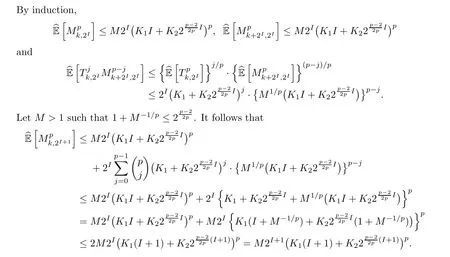
The proof is complete. □

Now we prove the law of the iterated logarithm.

Combining (5.8) and (5.9) yields (5.7). The proof is complete. □