具有Logistic增长和Crowley-Martin型发生率的随机SIRS 双流行病模型的动力学研究

赵彦军, 苏 丽, 孙晓辉, 李文轩

(1.吉林外国语大学国际商学院，长春 130117; 2.吉林大学数学学院，长春 130012)

0 引言

传染病一直是人类及一切生命的天敌，微分方程建模的方法是了解传染病传播机制和提供适当控制措施的有效途径。传染病的确定性模型于1927 年，由Kermack 和McKendrick[1]首次提出，称为SIR 模型，为以后传染病动力学的研究和疾病控制奠定了基础。很多研究者通过各种不同类型的数学模型，分析和研究了传染病在生物学、生态学、流行病学、族群动态和环境科学中的流行特征。在这些传染病流行模式中，通常将总人口分为易感者S、感染者I和恢复者R三类。现实生活中经常发生由于免疫性丧失，恢复的个体返回易感仓室的情况，这被归类为SIRS 模型[2–5]。例如疟疾、流感、肺结核等，个人的免疫力可能会随着时间的推移而减弱。

利用微分方程建模的方法研究传染病发展变化过程中，疾病发生率是一个至关重要的因素，其中最常用的为双线性(或标准)发生率。此外，Capasso 和Serio[6]首次引入感染者的饱和发生率βSI/(1+αI)，Xu 等[7–8]在SIR、SEIS 传染病模型中应用易感人群的饱和发生率βSI/(1+αS)，Miao 等[9–12]在SIS 等传染病模型中研究过Beddington-DeAngelis 发 生 率βSI/(1 +aS+bI)。当a=b= 0 时，Beddington-DeAngelis 发生率转变为双线性发生率；当a ＞0,b= 0 时，转变为易感者的饱和发生率；当a=0,b ＞0 时，转变为感染者的饱和发生率；因同时考虑易感者和感染者的双重抑制作用，Beddington-DeAngelis 发生率相对于双线性(或标准)发生率和饱和发生率，更具有一般性。1975 年，Crowley 和Martin[13]提出了Crowley-Martin 型发生率

它与典型的Beddington-DeAngelis 发生率相似。当α=β= 0 时，Crowley-Martin 型发生率转变为Holling I 型即双线性发生率；当β=0 时，其转变为Holling II 型即饱和发生率。此外，无论感染者是否感染易感者，Crowley-Martin 型发生率都允许感染者之间存在干扰[14–15]，从这个角度看，它优于Beddington-DeAngelis 型发生率，更具现实意义。

实际问题中，各种群的数量总是随着内部和外界环境扰动而变化，为使模型更贴近现实，经常假设种群数量具有Logistic 增长。此外，疾病发生率不仅与易感人群的数量有关，也与感染人群的数量有关。目前，对传染病模型这两个方面的研究已有很多成果[16–17]。在一般的流行病模型中，只有一种疾病是由一种病毒引起的，然而在现实生活中，更多情况下是多种疾病共存的。Meng 等[18–20]研究了具有双流行病的流行病模型。本文首先基于文献[5,13–20]的基础，提出一类具有Logistic 增长和Crowley-Martin 型发生率的确定性SIRS 双流行传染病模型

其中S(t)、I1(t)、I2(t)和R(t)分别表示在t时刻易感者、第1 种疾病的感染者、第2 种疾病的感染者和免疫者的数量。N(t) =S(t)+I1(t)+I2(t)+R(t)表示t时刻人口的总量，并且将所有新生儿均视为易感者，这里N(t)满足Logistic 增长；b为自然出生率系数；µ为自然死亡率系数；r=b −µ为内禀增长率系数；K为环境容纳量；β1、β2分别为第1 种疾病、第2 种疾病与对应病患者的接触率系数；θ1、θ2分别表示相应疾病的因病死亡率系数；η1、η2分别表示相应疾病的恢复率系数；δ为免疫者失去免疫再次成为易感者的丧失免疫率系数；ai和bi(i= 1,2)为测量抑制效果的参数，ai(i= 1,2)的生物学意义为处理时间，bi(i= 1,2)的生物学意义为感染者个体之间的干扰程度。假设模型(1)涉及的所有参数均为正数，基于生物学意义，本文仅在

内讨论模型的动力学性质，且假设(S(0),I1(0),I2(0),R(0))∈G。

易得确定性模型(1)的无病平衡点E0=(K,0,0,0)，且基本再生数

其定义为在完全无病的人群中放置一名感染者所产生的继发性病例的预期数量。一般来说，无论疾病是否发生，R0i(i=1,2)在其中起主导作用。如果R0i ＞1(i=1,2)，则确定性模型(1)存在唯一全局渐近稳定的地方病平衡点。

在现实生活中，某种生物在通常条件下，其生长受到一些小的随机因素的干扰，比如下一场小雨、刮一点风、天敌捕食一点、晴天变成阴天、正常的生老病死等，这些细小的、独立的随机干扰的总和，通常在数学上用“白噪声”来描述。环境噪声无处不在，疾病的传播过程不可避免的受到环境波动的影响。应用随机微分方程的稳定性理论来研究传染病动力学能更好地拟合现实情况，Arnold 等在文献[21–22]中首先对随机传染病动力学的研究做出了奠基性工作，随后国内外陆续涌现出大量的研究成果[3–5,9,11–12,14–20]。环境的改变会对传染病模型的参数产生一定的影响，因此为了更好地描述环境变化对疾病的影响，本文主要研究接触系数βi(i= 1,2)受到白噪声干扰时疾病的动力学行为，即βi →βi+σi˙Bi(t)(i= 1,2)，并且假设两种疾病不会重复感染(即患者感染一种疾病后就不会同时感染另一种疾病)，得到如下随机SIRS 双流行传染病模型

其中Bi(t)(i=1,2)为独立标准布朗运动，即随机干扰源；σi(i=1,2)为白噪声强度。将模型(2)中的四个方程相加，有

在本文中，设(Ω,F,{Ft}t≥0,P)是一个完备概率空间，σ-代数族{Ft}t≥0满足非降且右连续，并且B(t) = (B1(t),B2(t))是定义在完备概率空间(Ω,F,{Ft}t≥0,P)上的布朗运动。f(t)是[0,+∞)上的可积函数，定义

那么称疾病Ii(t)(i=1,2)是持久的。

1 全局正解的存在唯一性

为了研究传染病模型的动态行为，首先需要考虑其解是否具有全局正解。在本节中，首先证明模型(2)的等价模型(3)存在唯一的全局正解，进而说明模型(2)全局正解的存在唯一性。

定理1 对任意初值(N(0),I1(0),I2(0),R(0))∈G，随机模型(3)存在唯一全局正解(N(t),I1(t),I2(t),R(t))(t ≥0)，且该解依概率1 位于G中。

证明 因为模型(3)的系数满足局部Lipschitz 连续，但不满足线性增长条件，则对任意初值(N(0),I1(0),I2(0),R(0))∈G，模型(3)存在唯一的局部解(N(t),I1(t),I2(t),R(t)),t ∈[0,te), a.s.，其中te为爆破时间。要证明解的全局存在性，只需证明te=∞，a.s.。

这里令infϕ=∞(ϕ表示空集)。显然，当n →∞时，tn是单调递增的。令t∞=limn→∞tn，则显然有t∞≤te, a.s.。若t∞=∞, a.s.成立，则有te=∞，从而有(N(t),I1(t),I2(t),R(t))∈G,t ≥0, a.s.。换句话说，只需证明t∞=∞, a.s.即可。

我们采用反证法。若不然，则一定存在常数T ＞0 和ε ∈(0,1)，使得

则存在正整数n1≥n0，使得

定义C2→函数V:R4+→R1+∪{0}：

根据假设条件(H)，有

这里˜K是一个正常数，所以

对(5)式两端分别从0 到tn ∧T积分并取期望，得

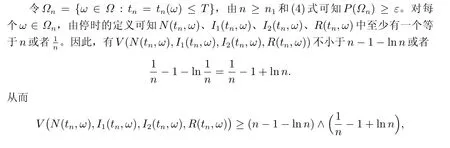
则由(4)式和(5)式，可知

其中1Ωn(ω)表示Ωk的示性函数。令n →∞，则有∞＞V(N(0),I1(0),I2(0),R(0))+˜KT=∞，矛盾，所以有t∞=∞, a.s.，这就意味着N(t)、I1(t)、I2(t)和R(t)以概率1 在有限时间内不会产生爆破。

2 疾病灭绝性的充分条件

本节我们将讨论模型(2)的随机灭绝性，研究传染病灭绝性的充分条件。

定理2 如果

则模型(2)的疾病几乎必然灭绝。

证明 设(S(t),I1(t),I2(t),R(t))是模型(2)满足初值(S(0),I1(0),I2(0),R(0))∈G的解，对模型(2)应用Itˆo 公式，有

因Mi(t)是满足初值Mi(0)=0 的局部鞅，根据鞅的强大数定理有

由模型(2)中的第二、第三个方程，可得

则有如下定理。

定理3 设(S(t),I1(t),I2(t),R(t))是模型(2)关于初值(S(0),I1(0),I2(0),R(0))的解，若R∗i ＜1 且

则模型(2)的疾病趋于灭绝，且limt→∞Ii(t)=0(i=1,2), a.s.。

证明 对(6)式两边从0 到t积分，有

所以limt→∞Ii(t)=0(i=1,2), a.s.。

由定理2 和定理3 表明，当白噪声扰动较大或R∗i ＜1(i= 1,2)且白噪声扰动不大时，疾病就会灭绝。

3 疾病在均值意义下的持久性

本节我们将讨论模型(2)的随机持久性，研究传染病持续下去的条件。

对(1+a1K)(lnI1(t)+b1I1(t))应用Itˆo 公式，有

对(11)从0 到t积分，并且两边同时除以t，再根据(10)式，有

由强大数定理可得limt→∞M2(t)/t=0，且I1(t)≤K，则

对(12)式取下确界再取极限，令t →∞,ϵ1→0，得

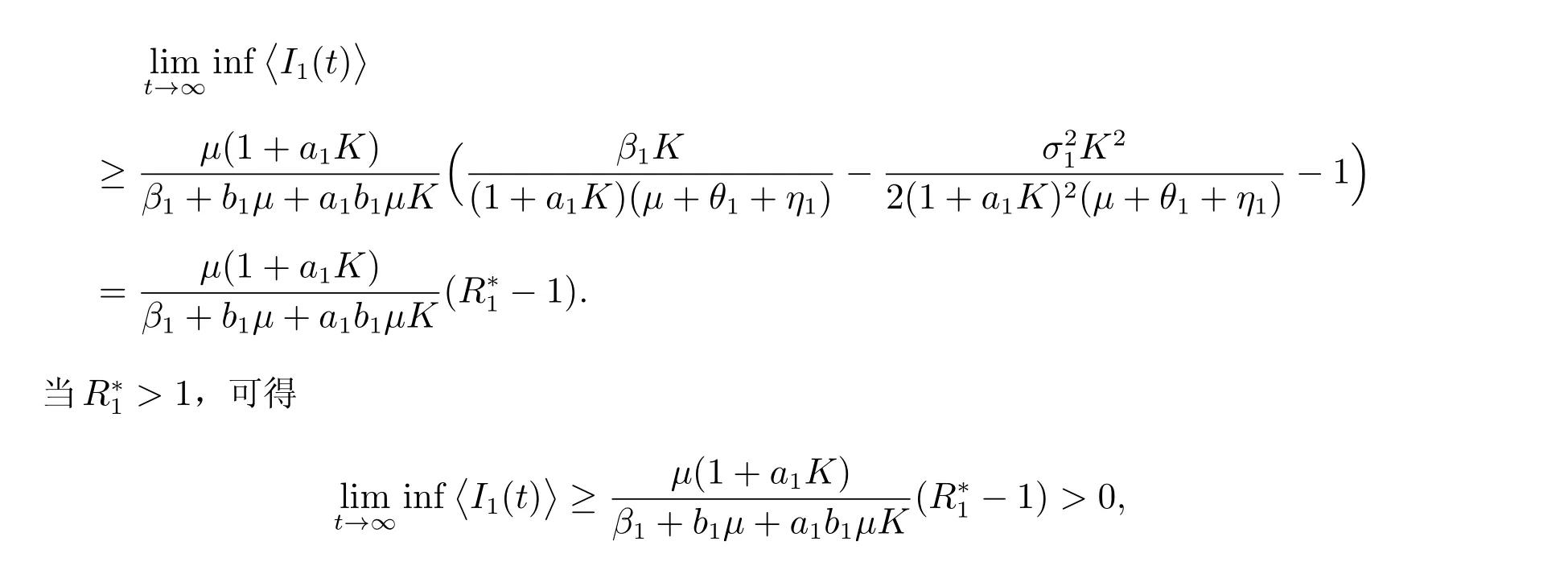
根据Itˆo 公式，有

对(14)式从0 到t积分，并且两边同时除以t，再根据(13)式，有

4 数值模拟

在这一部分，我们基于文献[5,18–20]的模拟数据，利用Matlab 进行数值模拟，验证本文结论的正确性。根据Milstein 方法，利用Matlab 对具有Crowley-Martin 型发生率的随机SIRS 双流行传染病模型(2)进行模拟，模型(2)的离散格式如下

其中ξi(k)(i=1,2,k=1,2,···,n)是独立的标准正态随机变量。

选择初值(S(0),I1(0),I2(0),R(0)) = (15,5,5,10)，参数取值如下K= 50,µ=0.2,β1=0.2,β2=0.2,θ1=0.1,θ2=0.1,δ=0.2,η1=0.2,η2=0.2,b=0.5,a1=0.2,b1=0.5,a2=0.2,b2=0.5,r=b −µ。

在图1 中，取σ1=0,σ2=0，此时即为确定性模型(1)，基本再生数R0i=1.818 12＞1(i=1,2)。由图1 可知，确定SIRS 模型(1)中疾病I1、I2将持续存在。在图2 中，取σ1=0.25,σ2=0.3，使得

图1 σ1 =0, σ2 =0

满足定理2 的条件。由定理2 的结论可知，此时无论R∗i(i=1,2)取值如何，随机SIRS 传染病模型(2)的疾病I1、I2将必然灭绝，这与定理2 的结论相吻合。

在图3 中，取σ1= 0.199,σ2= 0.205，使得R∗1= 0.999 98＜1,R∗2= 0.949 90＜1 且

图3 σ1 =0.199, σ2 =0.205

满足定理3 的条件。由定理3 的结论可知，此时随机SIRS 传染病模型(2)的疾病I1、I2将趋于灭绝，这与定理3 的结论相吻合。

在图4 中，取σ1=0.05,σ2=0.3，使得R∗1=1.766 53＞1 且

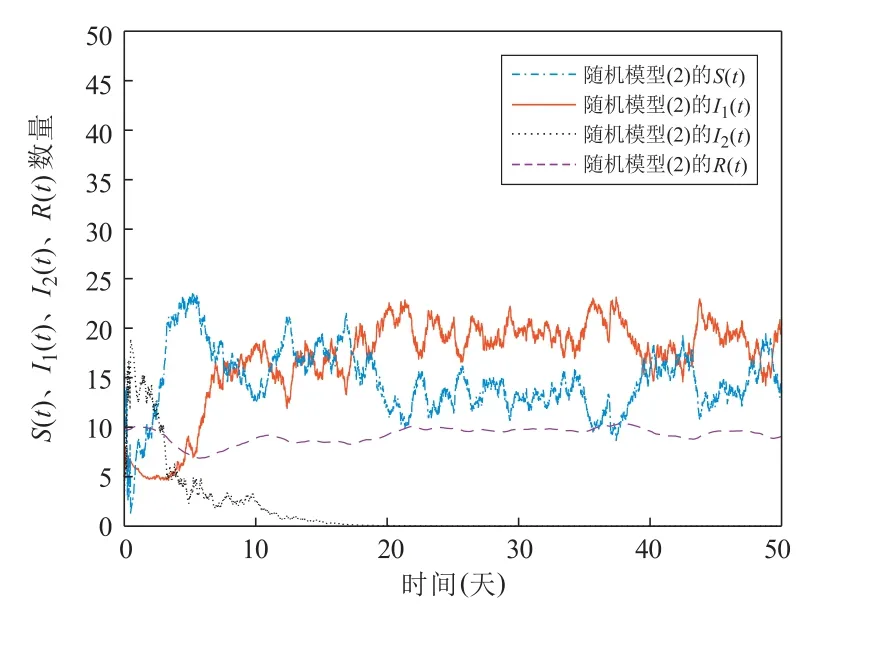
图4 σ1 =0.05, σ2 =0.3

满足定理4 中条件1)。由定理4 中条件1)的结论可知，此时随机SIRS 传染病模型(2)的疾病I1持久，疾病I2必然灭绝，这与定理4 中条件1)的结论相吻合。

在图5 中，取σ1=0.05,σ2=0.205，使得R∗1=1.766 53＞1,R∗2=0.949 90＜1 且

图5 σ1 =0.05, σ2 =0.205

满足定理4 中条件1)。由定理4 中条件1)的结论可知，此时随机SIRS 传染病模型(2)的疾病I1持久，疾病I2趋于灭绝，这与定理4 中条件1)的结论相吻合。

在图6 中，取σ1=0.25,σ2=0.08，使得R∗2=1.685 95＞1 且

图6 σ1 =0.25, σ2 =0.08

满足定理4 中条件2)的条件。由定理4 中条件2)的结论可知，此时随机SIRS 传染病模型(2)的疾病I1必然灭绝，疾病I2持久，这与定理4 中条件2)的结论相吻合。

在图7 中，取σ1=0.199,σ2=0.08，使得R∗2=1.685 95＞1,R∗1=0.999 98＜1 且

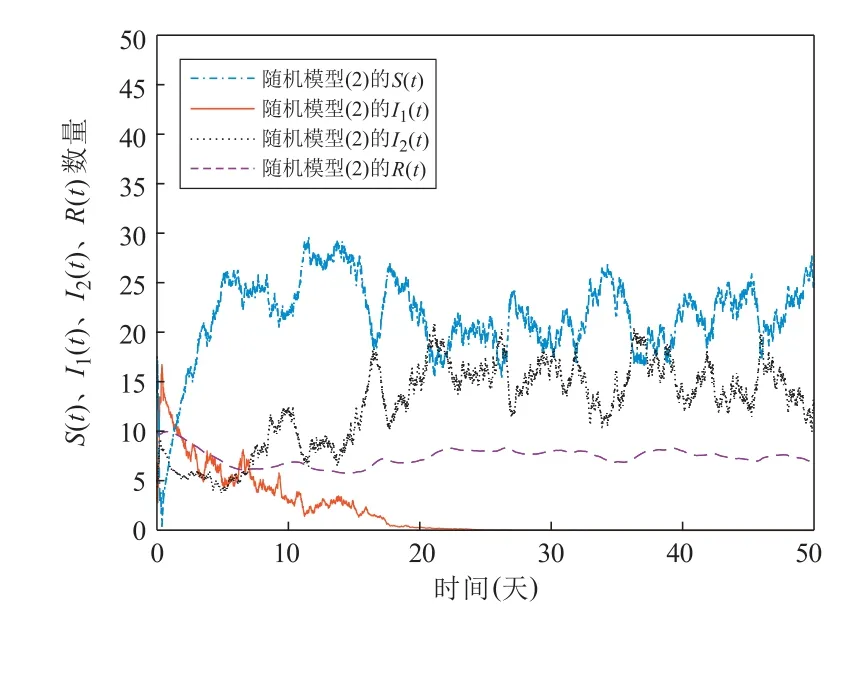
图7 σ1 =0.199, σ2 =0.08

满足定理4 中条件2)。由定理4 中条件2)的结论可知，此时随机SIRS 传染病模型(2)的疾病I1趋于灭绝，疾病I2持久，这与定理4 中条件2)的结论相吻合。

在图8 中，取σ1=0.05,σ2=0.08，使得R∗1=1.766 53＞1,R∗2=1.685 95＞1 满足定理4 中条件3)。由定理4 中条件3)的结论可知，此时随机SIRS 传染病模型(2)的疾病I1、I2将持续存在，这与定理4 中条件3)的结论相吻合。

图8 σ1 =0.05, σ2 =0.08

5 结论

疾病传播过程中，环境的随机波动是影响传染病传播的不可避免地重要因素之一。本文研究了一类利用白噪声来描述环境对疾病传播影响的随机SIRS 双流行传染病模型，得到了模型全局正解的存在唯一性、灭绝性和持续性的充分条件，结果表明：白噪声强度较大时两种流行病必然灭绝，而白噪声强度较小时，如果R∗i ＜1(i= 1,2)，两种流行病也会趋于灭绝，但如果R∗i ＞1(i= 1,2)，两种流行病在均值意义下将持续存在。本文结果在生物学意义下提供了疾病控制的理论和方法。最后，通过数值模拟验证了我们所得到的主要结果。