基于Copula的投资组合均值-CVaR有效前沿分析

金博轶

（上海财经大学 金融学院，上海 200433）

0 引言

自Markowitz在1952年创立投资组合理论以来，投资组合模型成为金融投资领域研究的热点问题之一。传统理论的一个重要缺陷在于其假设资产组合收益率服从多元正态分布，然而，大量的实证表明，这种假设经常与客观事实相违背。首先，金融时间序列多呈现时变波动、偏斜、高峰、厚尾等特性，用正态分布去近似变量的边际分布会产生较大的误差。其次，多元正态分布假设变量之间的相关关系为线性相关，然而，金融时间序列往往呈现尾部相关的特性。Ramchand和Susmel（1998）在研究全球主要股票市场的相关性后发现，当股价出现大幅波动时，市场之间的相关性会增加；Thierry和 Carole Métais（2009）研究了英国、德国、法国股票市场股价波动的联动效应并证实，市场之间的相关性呈现非对称特征，英国市场股价的波动对德国和法国的影响要强于德法对英国的影响；Longin和Solnik（2001）对五个主要国家股票指数的收益率进行研究并证实，市场之间的相关性在熊市会强于牛市。显然，基于线性相关关系的多元正态分布不能很好的扑捉到这种相关的时变性、非线性及非对称性特征。

为了克服多元正态分布的上述两点缺陷，本文拟使用Copula技术刻画资产组合联合收益率分布，在此基础上构建投资组合均值-CVaR模型，并使用蒙特卡罗技术对模型进行实证分析。

1 基于Copula的联合概率分布模型

Copula可以理解为 “相依函数”或 “连接函数”，通过Copula函数，我们可以将风险分解成单个金融资产的风险和由投资组合产生的相关性风险两部分。其中单个金融资产的风险可以由它们各自的边际分布来描述，而由投资组合产生的相关性风险则可以由连接它们的Copula函数来描述。因此，运用Copula理论构建资产组合收益率联合概率分布时分以下两步进行：（1）确定单个资产收益率边际分布；（2）选择适当的Copula函数，以便能较好地描述资产的相依结构。

1.1 边际分布的选择

金融时间序列的条件分布往往呈现出时变波动、波动集群、偏斜、尖峰、厚尾等特性，对这种特征进行最经典描述的是由Engle于1982年提出的自回归条件异方差模型（ARCH）；随后，学者们对该模型进行了推广，最重要的推广之一就是由Bollerslev于1986年提出的广义自回归条件异方差模型（GARCH）。大量实证研究表明，在股市中大多数情况下，GARCH(l，l)、GARCH(l，2)、GARCH(2，l)模型已能充分反映长时期的金融数据的波动特征。其中GARCH-t、GARCHGED模型对金融时间序列条件分布特性的刻画能力优于普通的正态GARCH模型，它可以较好地描述金融时间序列尖峰厚尾特性。因此，本文选用由t-分布噪声驱动的GARCH-t（1，1）模型来描述金融收益序列的条件边际分布。该模型的数学表达式为：

其中，Rt为收益率序列，μ为条件期望值，为条件异方差项，ω为随机项，εt为随机误差项，α和β为条件条件异方差方程的系数，tv为自由度为v的正规化t分布。

1.2 Copula函数的选择、参数估计及拟合优度检验

Copula函数种类繁多，不同的Copula能够刻画不同类型的相依特征。本文选择正态 Copula、t-Copula、frank-Copula、Gumbel-Copula、Clayton-Copula 等五种 Copula 类型进行实证分析与比较。

Copula技术的建模特点使其极适于采用多阶段参数估计法，本文的参数估计方法基于二阶段极大似然估计，第一阶段，估计边际分布的参数θ1：

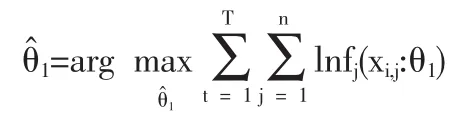
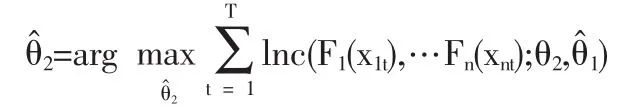
在估计出参数后，我们需要对拟合优度进行检验，本文用到的检验方法有下列两种。

(1）Kolmogorov-Smirno（K-S）检验

K-S检验的优点在于它是非参数或者是任意分布检验，它揭示了经验分布与理论分布之间的差别，检验统计量定义为：

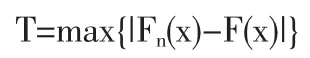
其中，Fn(x)代表累积经验分布函数，F(x)代表理论分布函数。

(2）AIC(BIC)信息准则

由于方法最优性的特点，赤池信息准则是建立在信息度量基础上的判断方法，它运用于检验极大似然估计的Copula模型；同时，可以使用贝叶斯信息准则（BIC）。虽然该方法不及最优性的特点，但是它对过度估计的模型能给予更灵敏的反应：

其中，k是 Copula参数个数，T是样本个数，AIC（BIC）的值包含了模型和参数估计值对数据的反应，AIC（BIC）越小，该模型拟合度越高。

2 CVaR及投资组合优化问题

CVaR是对传统的VaR风险度量方法的改进，它由Rockafellar等（2000）提出，CVaR可以定义为在一定的置信水平下，某一资产或资产组合超过VaR的损失的期望值。

假设某资产组合有n种资产，令f(x,y)代表组合损失（负的f(x,y)代表组合收益），其中向量x代表n种资产在组合中的比例，向量y代表n中资产的损失，假设y的分布密度为p(y)，则损失f(x,y)不超过一个给定值α的概率Ψ(x,α)为：

Ψ(x,α)是非减且右连续函数（Rockafellar，1970），在给定置信水平β∈(0,1)条件下，组合资产的VaR及CVaR分别为：

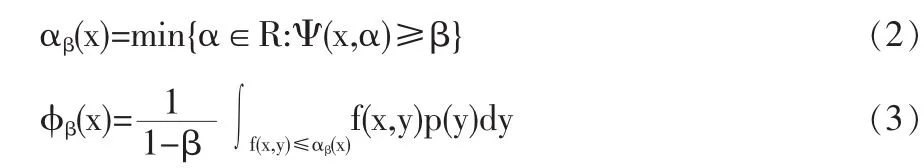
Rockafellar等（2000）认为，在收益率给定的情况下，组合的CVaR可以通过最小化下式得到：

式（4）也可以通过Mente Carlo模拟的方法近似的表述为：

其中，q代表模拟的次数，x=(x1,…,xn)代表资产组合中各种资产所占的比例，yk=(yk,1,…,yk,n)代表n种资产第k次模拟的收益率。并不一定可微，但是通过这种转换。该问题可以通过线性规划的方法非常简单的求解。

运用式（5）的Mente Carlo模拟技术，投资组合均值-CVaR模型可简化为：

为了下文比较的方便，我们不加证明地给出多元正态分布假设条件下的均值-CVaR模型的优化求解模型（刘小茂等2003）：

其中，rx为组合收益率，σ2(rx)为组合协方差矩阵，μ为期望收益率向量，e为单位向量，R为收益率临界值，c1(β)=Φ-1(β)为标准正态分布 N(0,1)的 β 下分位数 c2(β)=φ(c1(β))/(1-β),φ(·)为标准正态N(0,1)的概率密度函数。

3 实证分析

3.1 数据的选取与处理

我们选择沪深300指数里面四种不同行业的指数对上述模型进行实证分析。它们分别是沪深300的金融指数、能源指数、工业指数和消费指数。将价格{Pit}定义为第i种指数在第t日的收盘价，相应的将收益率{Rit}定义为Rit=100×(ln(Pit)-ln(Pit-1))。本文选取的样本时间分为两段，第一段从2003/06/18开始到2006/8/31，此段的有效数据共计737组，我们利用该段数据建立一个投资组合，分析其有效前沿。表1给出了在第一个时间段内四种行业指数的基本数字特征；第二段从2006/8/31开始到2009/4/31，在这段时间，我们通过资产组合的动态调整来考察组合的整体表现。本文数据来源于WIND金融资讯，数据处理所用到的软件有excel、R2.8.1以及lingo9.0。

从表1可以看出，四种指数收益率的J-B指标均为1，意味着上述四种行业指数的收益率显著异于正态分布的假设。峰度均大于或接近于3，说明具有尖峰特征；偏度均大于0，说明收益率序列具有右偏特征。

表1 四种指数的的基本数字特征

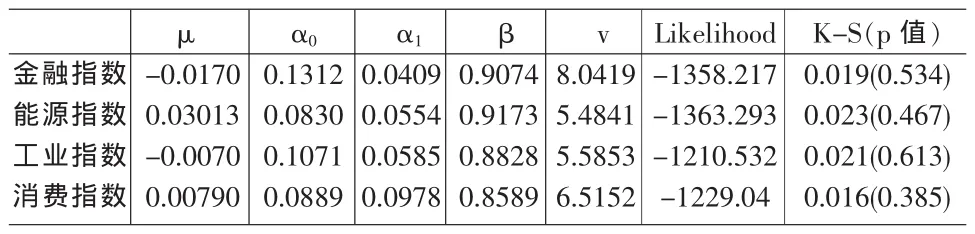
表2 t-GARCH（1，1）拟合结果

3.2 Copula参数估计

首先使用t-GARCH（1，1）模型估计出的股票收益率边际分布参数（见表2）。

在估计出边际分布的参数之后，就可得到下一期收益率RT+1的条件分布：

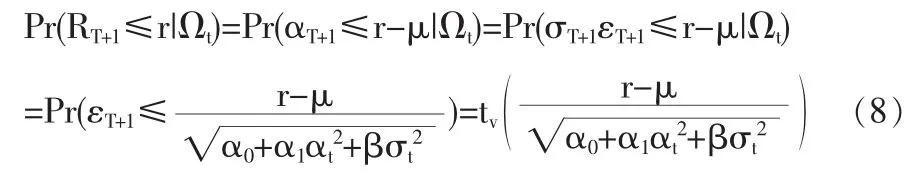
其中，tv(·)为自由度为v的t-分布，Ωt为时刻T为止的信息集。

根据得到的各样本收益率序列边缘分布对原序列做概率积分变换，使用变换后的数据进行第二阶段估计，表3及表4给出了Copula函数参数估计值及拟合优度检验结果。

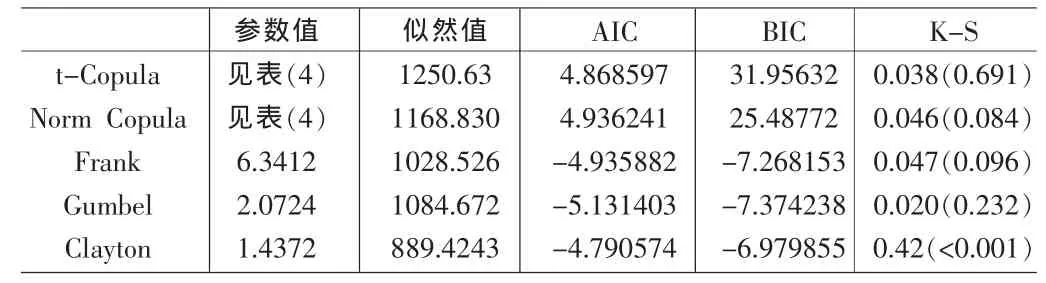
表3 Copula函数的参数估计及拟合优度检验

分析表3，从K-S指标上看，除 Clayton Copula外，其余四种Copula的 K-S指标通过了5%的显著性水平检验，t-Copula函数K-S指标的p值最大，这表明与其他四种Copula相比，它能更好的拟合真实的经验分布，但是AIC及BIC指标却支持Gumbel-Copula，可能的原因是t-Copula需要估计7个变量值；另外，阿基米德类Copula一般只适宜于刻画两个变量的相依结构，对描述多变量的相依结构意义不大。因此，我们最终选择t-Copula做为下一步随机数模拟的生成函数。

3.3 蒙特卡洛模拟收益率

表4 Copula相关系数矩阵

在完成了Copula模型参数估计后，下一步的任务就是生成满足选定Copula函数的随机数，基于t-Copula函数的模拟算法为:

（1）求出相关矩阵∑的 Cholesky分解矩阵A，即 ATA=∑。

（2）生成服从 N(0,1)的相互独立的随机变量 z1，z2，z3，z4。

（4）令 b=Az,z=(z1,…z4)T。

（6）uk=tv(ck)(k=1,…4),tv表示自由度为v标准t分布函数。

（7）xk=Fk-1(uk)(k=1,2,3,4)，其中 Fk-1(·)为 k 种指数条件边际分布的反函数。

3.4 优化问题求解

在完成了第二步的随机模拟之后，接下来我们就可以利用lingo9.0软件非常容易的求解式（6）的优化问题。图1给出了基于Copula方法的均值-CVaR投资组合有效前沿及多元正态分布假设条件下的均值-CVaR投资组合有效前沿。

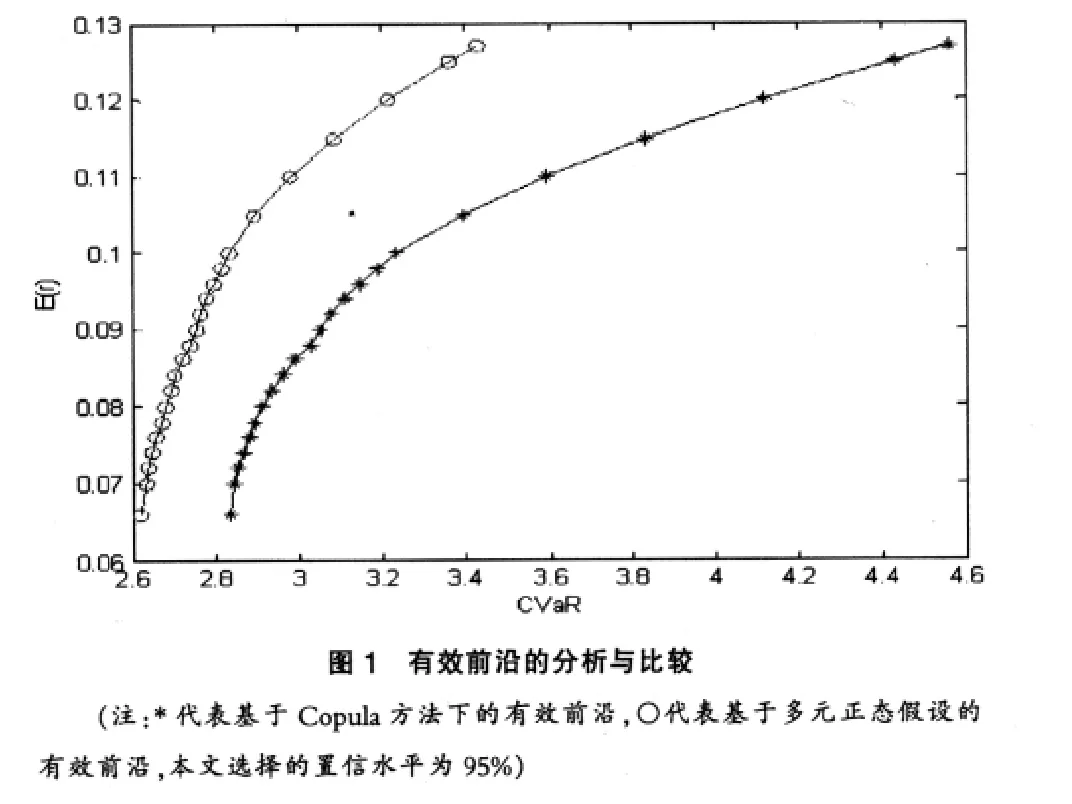
分析图1我们可以得到以下两点结论：

（1）与Copula-均值-CVaR模型下的投资组合相比，基于多元正态分布假设的投资组合将会在收益一定的条件下低估风险或在风险一定的条件下高估收益。究其原因主要有以下两点：其一，传统理论将资产收益率的边际分布假设为服从正态分布；然而，金融数据往往具有尖峰、厚尾的特征，正态近似将会低估单个资产的下尾风险；其二，传统正态假设基于线性相关，但是，资产组合收益率往往呈现尾部相关的特征，即在市场价格发生大幅波动时，资产之间的相关性会增加，从而造成组合整体收益率与线性相关假设相比发生更大幅度的波动。总之，运用多元正态假设构建投资组合将会低估组合的整体风险水平。Copula函数对资产组合收益率的边际分布没有限制，而且可以较好的扑捉组合资产之间相关关系的非线性特征。因此，基于Copula的联合概率分布模型能够更加准确的反映资产组合的风险状况。

（2）尾部相关性会提高资产组合的风险溢价，即由于尾部相关关系的存在，投资者将会要求更高的风险溢价来弥补资产之间相关性在熊市增加的风险。

3.5 投资组合的动态调整与比较

下面要回答的另一个非常重要的问题是：基于Copula模型下的投资组合的表现是否会优于基于多元正态假设下的投资组合？由于Copula模型能够较真实的反映资产组合的风险状况，因此，我们预测，基于Copula模型的投资组合的整体表现会优于正态分布假设的投资组合。为了检验我们的预测，现在考虑资产组合的一个动态调整过程，假设资产组合的建仓时间为2006年8月31日，初始价值为1，以后每两个月根据新的交易数据运用上述两种模型对组合中各种资产所占的比例进行一次调整，在允许卖空、不考虑交易费用及市场摩擦等因素的条件下，图2给出了从2006/8/31到2009/4/31这个时间段两种组合总价值的变化情况。

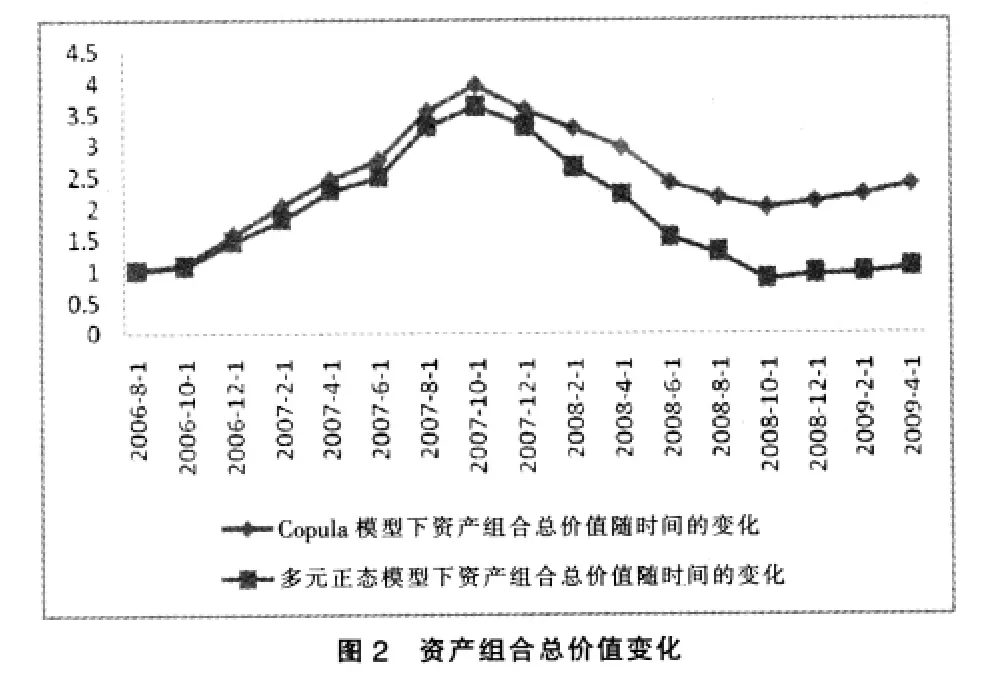
从图2可以看出，在股市处于牛市阶段（即从2006年8月31日到2007年11中旬），两组资产组合的总价值都有不同程度增加，然而，Copula模型下的资产组合总价值增幅更大一些；从2007年11中旬开始，股市进入熊市，两种资产组合的总价值都发生了缩水，然而，Copula模型下资产组合的总价值下降幅度远小于多元正态模型下的组合。可能的原因是我国股票市场存很显著的羊群效应（刘文虎，2009），投资者容易随价格波动出现追涨杀跌行为，从而使市场价格波动过度，造成市场的不稳定。Copula模型下的上尾及下尾相关系数能够较好地量化这种效应，从而使投资者充分抓住牛市的上涨机会，降低资产组合在熊市的缩水幅度。

4 结语

鉴于传统多元正态分布在描述资产组合联合分布上存在的缺陷，本文构建了基于Copula理论的投资组合均值-CVaR模型，采用Copula建模的优势在于其可以将单个资产收益率的边际分布和资产之间的相关结构分开讨论，单独处理，从而大大降低了分析问题的难度，增强了金融建模的灵活性。本文得出以下两点重要结论：

（1）与Copula-均值-CVaR模型下的投资组合相比，传统基于多元正态分布假设的投资组合策略将会低估风险或高估收益。

（2）对单个资产下尾风险及资产组合尾部相关风险的有效控制使Copula模型下的资产组合的整体表现好于正态分布假设下的资产组合。

总之，将Copula理论应用于投资组合的管理过程中能够使投资者在有效控制组合风险条件下增加组合的收益率。

[1]Ramchand,L.,R,Susmel.Volatility and Cross Correlation across Major Stock Market[J].Journal of Empirical Finance，1998,(5).

[2]Thierry Ané,Carole Métais.The Distribution of Realized Variances:Marginal Behavior Asymmetric Dependence and Contagion Effects[J].International Review of Financial Analysis，2009，20.

[3]F Longin-B Solnik.Extreme Correlation of International Equity Markets[J].Journal of Finance,2001，（2）.

[4]Sklar A.Fonctions de Repartitionàn Dimensions et Leurs Marges[J].Publication de l’Institut de Statistique de l’Université de Paris,1959，(8).

[5]Nelsen,R.An Introduction to Copulas[M].New York:Springer,1999.

[6]Rockafellar,R.T.Convex Analysis,Princeton Mathema-Tics[M].New Jersey:Princeton University Press，1970，（28）.

[7]Artzner,P.,Delbaen,F.,Eber,J.M.,Heath,D.Coh-Erent Measures of Risk[J].Mathematical Finance,1999,(9).

[8]Rockafellar,R.T.,S.Uryasev.Optimization of Conditional Value-at-Risk[J].Journal of Risk,2000,(2).

[9]刘小茂,李楚霖,王建华.风险资产组合的均值-CVaR有效前沿(Ⅰ)[J].管理工程学报,2003,(1).

[10]刘文虎.基于Malmquist指数的中国股市羊群效应测度研究[J].证券市场导报，2009，（9）.