一个不等式问题的简证及其思考
2010-11-25 08:12
中学教研(数学) 2010年12期
●
(咸阳师范学院基础教育课程研究中心 陕西咸阳 712000)
在《数学通报》1992年第10期的数学问题栏目中,黄汉生先生提出了如下不等式:
问题1已知x,y,z∈R+,求证:
原刊物的证明过程比较复杂,下面笔者给出该题的简化证明.
证明注意到简单不等式ab+bc+ca≤a2+b2+c2,得
即

因为

所以

由柯西不等式,得
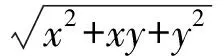



得证.
对不等式(1)进行变形,可等价转化为:
问题2已知x,y,z∈R+,求证:
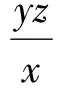
事实上,还可以证明如下的不等式:
问题3已知x,y,z∈R+,求证:

证明利用二元均值不等式得
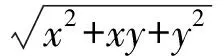
即

同理可得

将这3个不等式叠加,立得不等式(3).
链接不等式(2)和(3),可得如下不等式链:
问题4已知x,y,z∈R+,求证:
显然,不等式(4)是如下常见不等式的加细.
问题5已知x,y,z∈R+,求证:
在《中学数学月刊》2008年第1期中,田富德先生提出了这样一个分式不等式:
问题6若a,b,c∈R,且a,b,c都不为0,则
事实上,不等式(6)等价于

我们知道,a2+b2+c2≥ab+bc+ca,于是有比不等式(6)更强的结论:
若a,b,c∈R,且a,b,c都不为0,则
这正是问题5中的不等式!以上我们探讨了不等式(5)的一种加细,得到了比较优美的不等式(4).这里需要指出的是,不等式还有一些简单的应用,请看如下不等式:

(W.Janoux 猜想)
提示:对分母进行换元z+x=a,x+y=b,y+z=c,所证不等式等价于不等式(5).

提示:对分母进行换元,得所证的不等式等价于不等式(5).
猜你喜欢
新高考·高三数学(2022年3期)2022-04-28
中学生数理化·七年级数学人教版(2021年12期)2021-12-31
音乐天地(音乐创作版)(2020年3期)2020-06-09
中国卫生质量管理(2019年5期)2019-10-24
作文世界(小学版)(2017年11期)2018-03-07
中学教学参考·理科版(2017年8期)2018-02-24
中文信息(2017年12期)2018-01-27
中学生数理化·高三版(2017年2期)2017-04-21
福建中学数学(2017年1期)2017-04-21
中央民族大学学报(自然科学版)(2015年2期)2015-06-09

