Jo rdan李代数的分解与Frattini理论
温启军,钱 玲,陈良云
(1.长春大学理学院,吉林长春 130022; 2.东北师范大学数学与统计学院,吉林长春 130024)
Jo rdan李代数的分解与Frattini理论
温启军1,钱 玲2,陈良云2
(1.长春大学理学院,吉林长春 130022; 2.东北师范大学数学与统计学院,吉林长春 130024)
证明了中心为零的Jordan李代数能够分解成不可分解理想的直和,这种分解在不计理想次序的前提下是唯一的,并运用Jo rdan李代数的Engel定理,得到了Jo rdan李代数的Frattini子代数的若干性质和幂零Jordan李代数的几个判定方法.
Jo rdan李代数;Engel定理;分解唯一性;Frattini理论
1 预备知识
基于对李代数、李超代数和Jordan代数的研究,Susumu Okubo提出了Jordan李超代数的概念[1-2]:设J是一个Z2阶化向量空间,记为

易见当δ=1时,Jordan李代数就是通常所说的李代数,也就是说Jordan李代数更具有广泛性.
本文将着重论述Jordan李代数分解的唯一性问题.众所周知,特征0域上的半单李代数可以分解成单李代数的直和[4-5].代数称为不可分解的,如果它不能分解成理想的直和[6-7].在本文中,我们将证明中心为零的Jordan李代数能够分解成不可分解理想的直和,这种分解在不计理想次序的前提下是唯一的.文献[3]给出了Jordan李代数Engel定理的证明,本文运用Jordan李代数的Engel定理,得到了Jo rdan李代数的Frattini子代数的一些结果.
2 主要结果
定义1如果一个Jordan李代数J的自同态φ满足φadx=adxφ,∀x∈J,则φ称为J的J-自同态.
引理1令J是域F上的Jordan李代数,则下列命题成立:
(1)若f,ɡ是J的J-自同态,则f+ɡ与fɡ也是J的J-自同态;


定理2[4]设V是域F上的有限维向量空间且f是作用在V上的线性变换.若X是满足X(f)=0的多项式.则:
(1)若X=q1·q2且q1,q2互素,则V=U⊕W,U和W是f的不变子空间,且满足q1(f)(U)=q2(f)(W)={0};
(2)V=V0⊕V1,V0和V1是f的不变子空间,且满足f|V0是幂零的,f|V1是可逆的.
注1(1)若V是有限维的,则f存在特征多项式X.定理2中的(2)分解成为f的Fitting分解. V0与V1分别称为Fitting-0和Fitting-1.
(2)设J是域F上的有限维Jordan李代数.设(ada)j(x)=0},∀a∈J,i∈N.则A=[a,A]与(ada)n(B)={0},∃n∈N.由定理2得J=A⊕B.若ada不是幂零的,则A与B都非零.
定理3[3](Engle定理)设J是有限维Jordan李代数,则J是幂零的当且仅当∀x∈J,x是ad-幂零元.
设J是有限维Jordan李代数,定义F(J)是J的所有极大子代数的交和ψ(J)是包含在F(J)且是J的理想中的最大理想.
引理6设J是有限维Jo rdan李代数,则有:
(1)F(J)⊆J(1),J(1)=[J,J];
(2)如果H是J的子代数,并且H+F(J)=J,则H=J.
证明(1)如果J=[J,J],显然有F(J)⊆J(1).
如果J≠[J,J],反证.假设x∈F(J),并且x∉J(1),不妨令dimJ=r.
我们可以构造J的(r-1)维子空间N,并且N⊇J(1),x∉N,由N的维数显然有N是J的一个极大子代数.但由x∈F(J)知x是属于任何一个极大子代数的,当然就有x∈N,这就产生了矛盾.所以F(J)⊆J(1).
(2)反证.若H≠J,则有J的一个极大子代数N,使得H⊆N.于是F(J)⊆N.由于J=H+F(J)⊆N,所以N=J.这与N是极大子代数矛盾.从而H=J.
引理7若J是域F上的一维Jo rdan李代数,且ch F≠3,则[J,J]=0.
证明由于J是一维的,所以不妨设x∈J,J=Fx.因为ch F≠3,由Jacobi等式知[x,[x,x]]=0.设[x,x]=λx,λ∈F.则
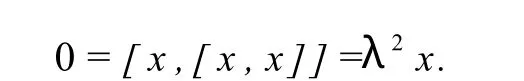
因此λ=0,即[x,x]=0.从而J是可交换的.
引理8设J是域F上的有限维幂零Jo rdan李代数,ch F≠3.则有:
(1)J的每一个极大子代数M也是J的理想;
(2)F(J)=J(1).
证明(1)因为J幂零,所以存在n∈N和一个理想序列,满足
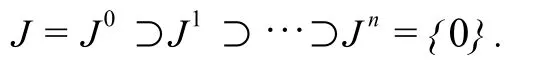
于是由M≠J,知存在m∈N,使得Jn+M≠M,并且Jn+1+M=M.于是∃x∈J,满足x∈Jn且x∉H.从而有即M是J的理想.
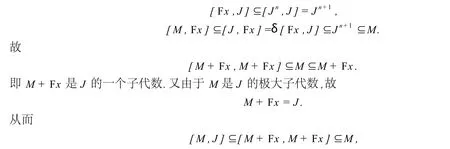
(2)由结论(1)可知,J的任何极大子代数M都是J的理想.于是J/M没有真子代数,也没有真理想,从而J/M只能是一维的.由引理7知J/M是可交换的,即因为M是J中任意的极大子代数,故J(1)⊆F(J).由引理6,F(J)⊆J(1)知F(J)=J(1).
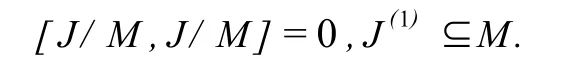
引理9设J是域F上的Jordan李代数且ch F≠3.设A是J的理想,B是A的理想,且B⊆A∩F(J).若A/B幂零,则A也幂零.特别的,若A是J的理想且A⊆F(J),则A是幂零的,φ(J)是J的幂零理想.
利用定理2的引理9及文献[5]中定理2.12的方法,易证下面的定理:
定理4设J是域F上的Jordan李代数且ch F≠3,则下列命题等价:
(1)J幂零;
(2)∀x∈J,adx幂零;
(3)J/C(J)幂零;
(4)若A是J的理想且满足A⊆φ(J),则J/A幂零;
(5)J的每个极大子代数H也是J的理想;
(6)F(J)=φ(J)=J(1).
[1] SUSUMU OKUBO.Jordan-Lie super algebra and jordan-Lie triple system[J].Journal of Algebra,1997,198:388-411.
[2] GRISHKOV A N.Speciality of Lie-Jordan algebra[J].Journal of Algebra,2001,237:621-636.
[3] 钱玲.Jordan李代数的Engle定理及其应用[D].长春:东北师范大学数学与统计学院,2010.
[4] STRADE H,FARSTEINER R.Modular Lie algebras and their rep resentations[M].New York:Marcel Dekker Inc,1988:300.
[5] 孟道骥.复半单李代数引论[M].北京:北京大学出版社,1998:56-88.
[6] 陈良云,张永正.关于限制李超代数的分解[J].数学物理学报,2007,27(4):577-582.
[7] 吴险峰.低维李超三系的分类[J].吉林大学学报:理学版,2009,47(3):671-676.
On the decom position and Frattin i theory of Jordan L ie algebras
W EN Qi-jun1,Q IAN Ling2,CHEN Liang-yun2
(1.School of Sciences,Changchun University,Changchun 130022,China; 2.School of M athematics and Statistics,Northeast No rmal University,Changchun 130024,China)
This paper w ill p rove that a Jordan Lie algebra satisfyingC(J)={0}can be decomposed into direct sum of indecomposable ideals and this decomposition is unique up to the order of the ideals,give its Frattini theo ry and obtain some sufficient and necesary conditions of nilpo tent Jo rdan Lie algebras using Engel's theorem of a Jordan Lie algebra.
Jordan Lie algebras;Engel's theorem;uniqueness of the decomposition;Frattini theory
O 152.5
110·21
A
1000-1832(2010)04-0012-05
2010-05-27
国家自然科学基金资助项目(10701019,10871057);中央高校基本科研业务费专项资金资助项目.
温启军(1973—),男,硕士,讲师;通讯作者:陈良云(1974—),男,博士,副教授,主要从事李代数研究.
(责任编辑:陶 理)

