求变截面梁位移方法的研究

贾建国,李长辉,武振亚

(1.中铁六局集团天津铁路建设有限公司,天津300232;2.天津大学,天津300072)

在求解梁的位移时,对于抗弯刚度EI为常量的等直梁,求解的方法很多,而对于变截面梁国内外的文献研究很少。本文提出了求变截面梁位移的单位力法、积分法、最小势能原理法,这对于实际工程应用以及理论研究都具有很好的参考价值。

1 求变截面梁位移的方法

1.1 单位力法求位移

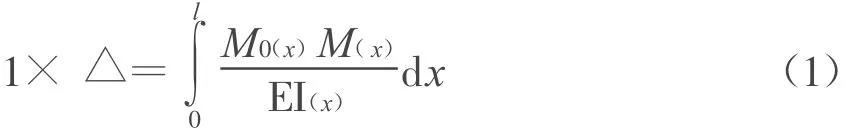
式中1—广义力;△—与广义力相对应的广义位移;M0(x),M(x)—单位力及荷载作用下引起的任意x截面的弯矩。

1.2 积分法求位移

在用积分法求梁的挠曲线方程时,所有的材料力学教材中阐述的均为抗弯刚度EI为常量的等直梁。但是,在实际工程中往往遇到变截面梁,即EI(x)为变量的梁。下面给出求解变截面梁挠曲线方程的一般方法。对于变截面梁,挠曲线近似微分方程为EI(x)=M(x)因此

对式(2)连续积分二次,可得到变截面梁挠曲线方程的一般表达式y(x)

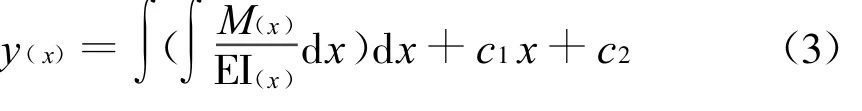
依据上式,就可以求出变截面梁任一截面的挠度和转角,从而可进行梁的刚度校核。由上述变截面梁的挠曲线方程的求解过程可见与等直梁类似,只不过任一截面对中性轴的惯性矩I(x)是个变量,积分时比等直梁复杂。

1.3 最小势能原理求位移

变截面梁的总势能为

式中U—变截面梁的应变能;W—变截面梁上的荷载所做的功;Π—Cm的函数,(m=1,2,3,…,n)。

根据最小势能原理有

变截面梁在荷载作用下挠曲线方程可预先定为y(x)

y(x)必须满足变截面梁的位移边界条件,当同时满足力的边界条件时,求出的临界力就逼近精确解。将式(6)代入式(5),将给出Cm的m个线性代数方程,这样,就可以求出C1,C2,C3,…,Cn,从而得到y(x)的表达式。n值越大,y(x)的值就越接近于精确解。

变截面梁的应变能U的计算公式为

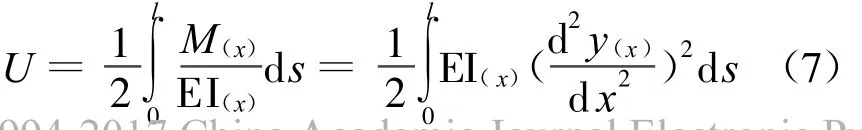
U的计算与等截面梁不同的I(x)是个变量,求解较复杂。

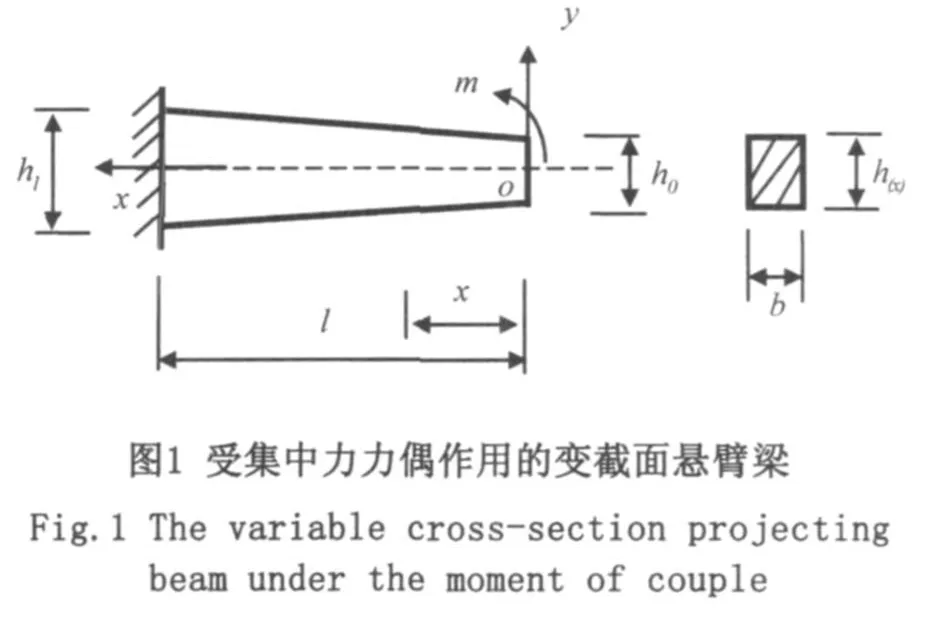
2 算例

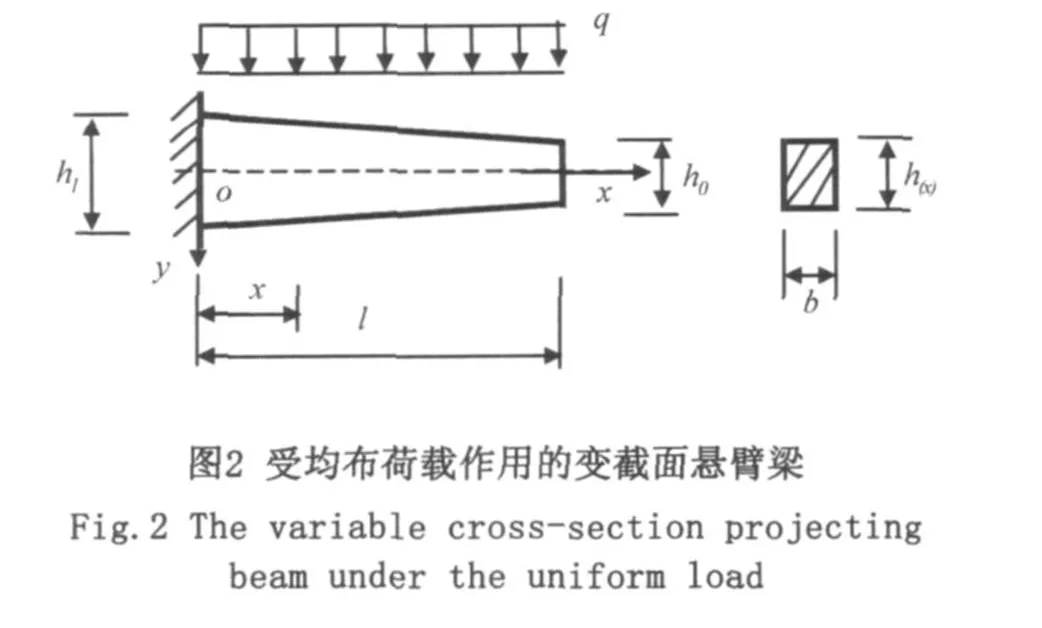
如图1所示的变截面悬臂梁,在自由端受到外力偶矩m作用,试分别用单位力法、积分法求该梁自由端的挠度。

2.1 单位力法求图1梁的挠度

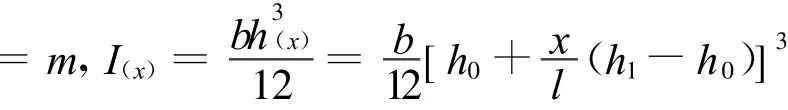
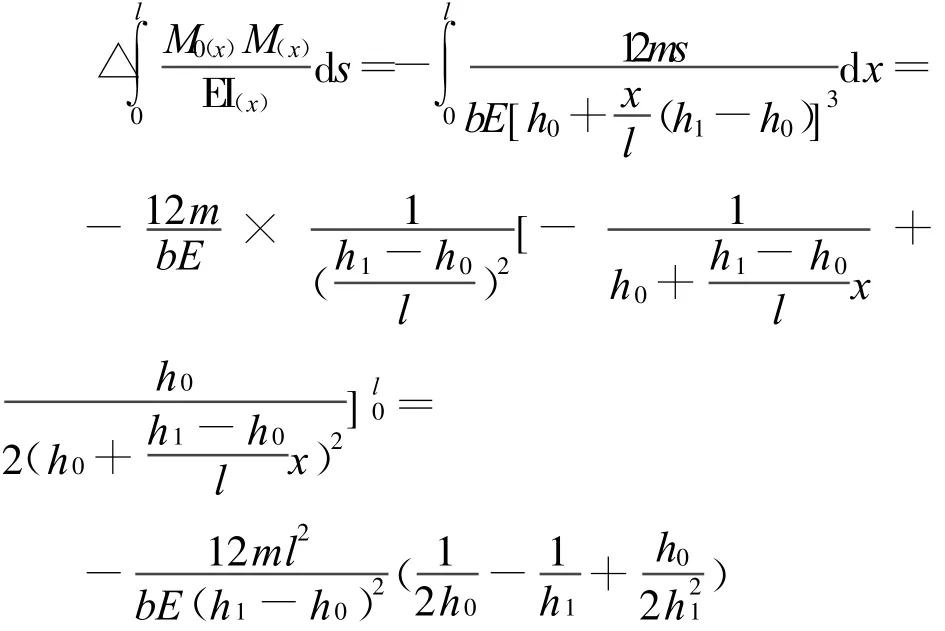
这就是其精确解。

2.2 积分法求图1梁的挠度

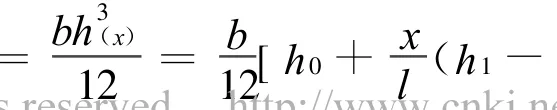
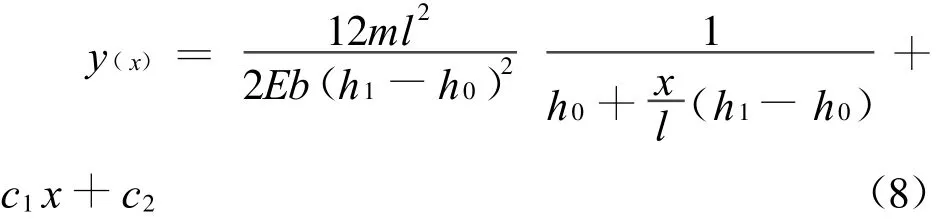
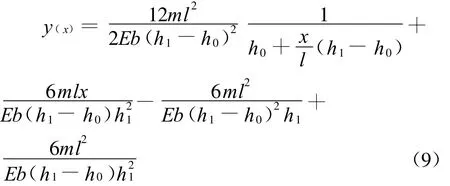
2.3 最小势能原理求图2梁的挠度

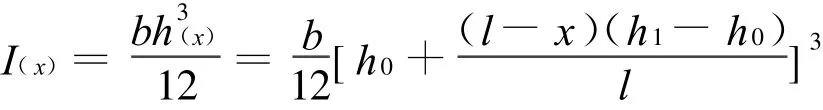
设y(x)=C2x2,在边界上满足变截面梁的位移边界条件,由所假设的位移函数,按下式可求出该变截面梁的总势能为

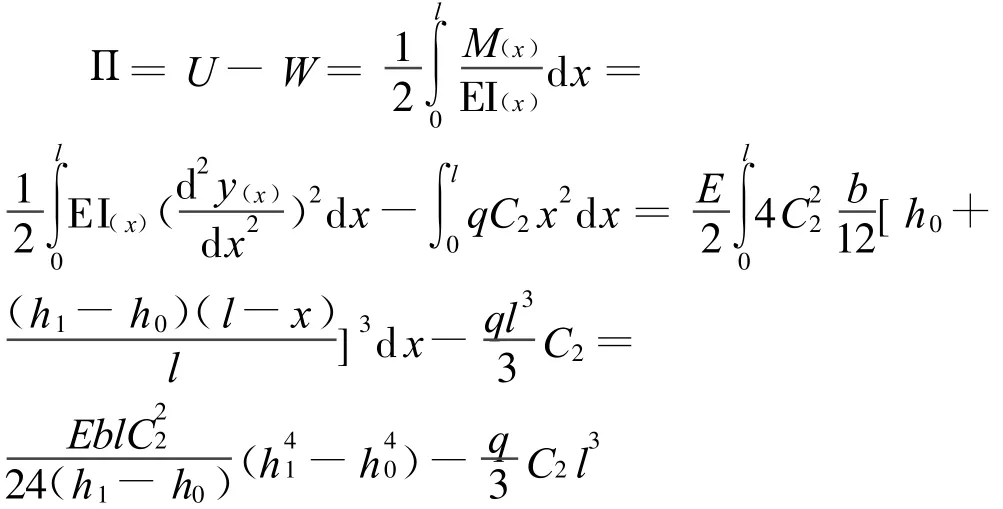
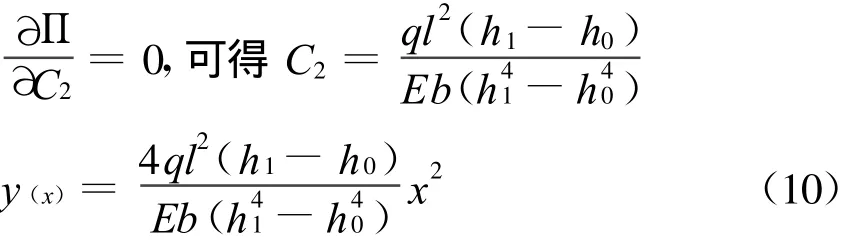
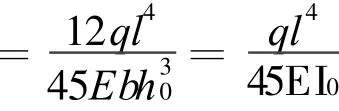
为了提高计算精度,设y(x)=C2x2+C3x3,在边界上满足变截面梁的位移边界条件,将y(x)对x求二阶导数代入Π的计算公式进行运算,得该变截面梁的总势能为

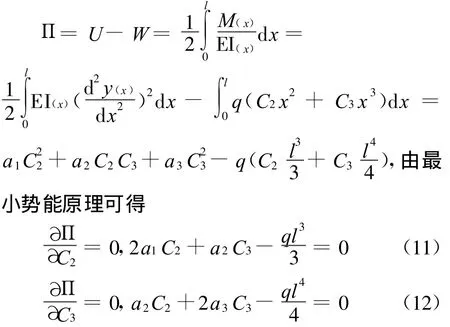
由(11)、(12)两式解得

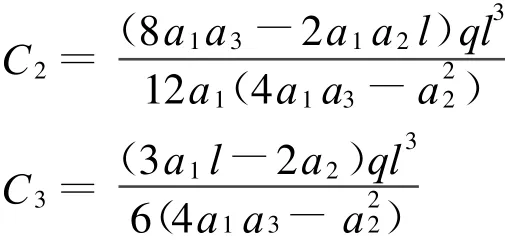
所以,该变截面梁的挠曲线方程为

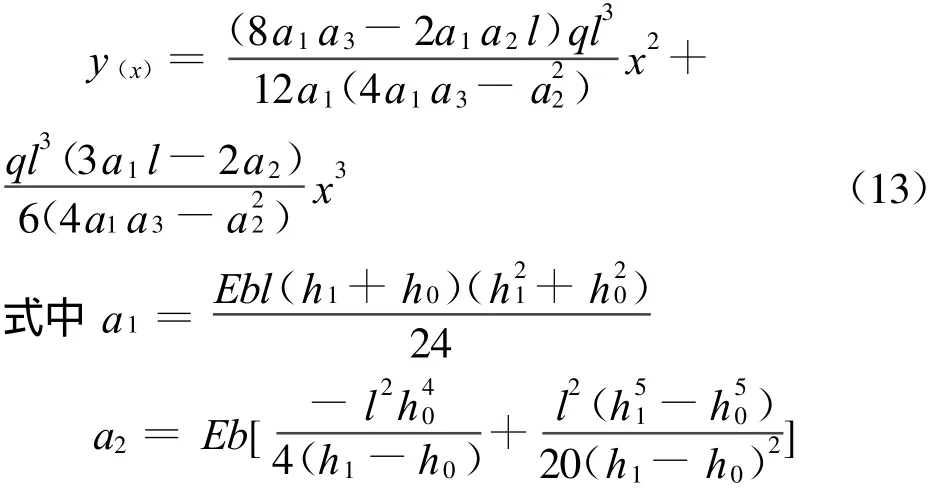
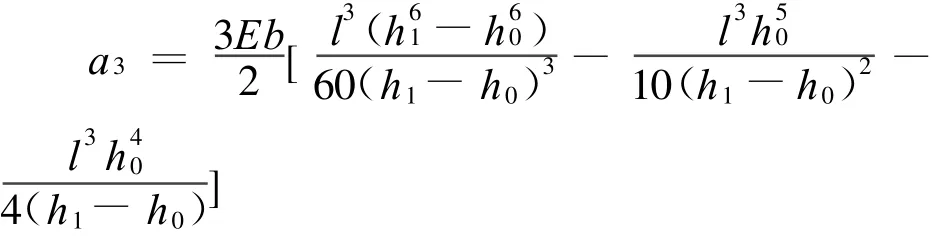
利用式(13)求解就比利用式(10)求解更接近精确解。

当h1=2h0,x=l时,由式(13)求得变截面梁自由端的挠度为

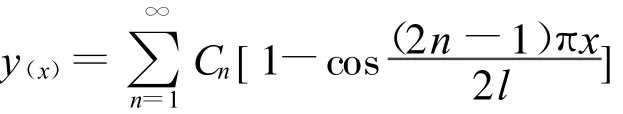
3 结论

本文所给出的单位力法、积分法、最小势能原理法,都是求解变截面梁很好的方法,其中单位力法、积分法为精确的方法,最小势能原理法为近似方法。单位力法可以很快求出变截面梁的某个截面的挠度和转角的精确解;积分法可以求出变截面梁精确的挠曲线方程,根据挠曲线方程可求出任一截面的挠度和转角的精确解,对理论研究很有意义。

[1]王世斌.材料力学[M].北京：高等教育出版社,2008.

[2]孙训方.材料力学(Ⅱ)[M].北京：高等教育出版社, 2002.

[3]徐杏华.基于最小势能原理的悬臂梁弯曲研究[J].陕西理工学院学报,2009,25(1)：12-16.

[4]李自林.变截面构件受冲击荷载作用时动应力的计算[J].河北建筑科技学院学报,1999,16(4)：6-9.