弹性接触问题的快速算法及其在圆锥滚子接触应力分析中的应用

米俊，夏伯乾

(郑州大学 机械工程学院，郑州 450001)

接触问题是滚动轴承寿命设计中的基本问题，对滚子轴承而言，由于滚子和滚道之间的接触是有限长线接触，而且滚子端部有应力集中，因此经典的求解滚子轴承接触问题的Hertz线接触理论就无法得到理想的结果。对非Hertz接触问题，目前广泛地采用数值解法。数值分析的手段有2类：一是使用有限元软件，如ANSYS，Nastran，I-DEAS等；二是使用经典的数值分析方法，即在二维区域内对接触问题的积分方程进行数值求解。用有限元软件分析滚动轴承的接触问题，过程复杂、占用计算资源较多，很不经济，所以现实中大量关于滚动轴承接触问题的分析与研究仍然广泛应用经典的数值分析方法。

圆锥滚子由于几何形状的复杂性，关于其接触应力计算与分析方面的研究文献还比较少。文中将一种求解弹性表面接触问题的快速直接迭代算法[1]应用于圆锥滚子接触应力的求解，得到了不同载荷下圆锥滚子的中心接触应力分布，为圆锥滚子轴承的优化设计提供参考。

1 弹性接触问题的基本方程

弹性体A和B在外加载荷F作用下相互接触，如图1所示。在这里先作如下假设：(1)接触体之间的摩擦可以忽略不计；(2)接触体几何尺寸远大于接触区域的几何尺寸；(3)接触区域视为平面。则有

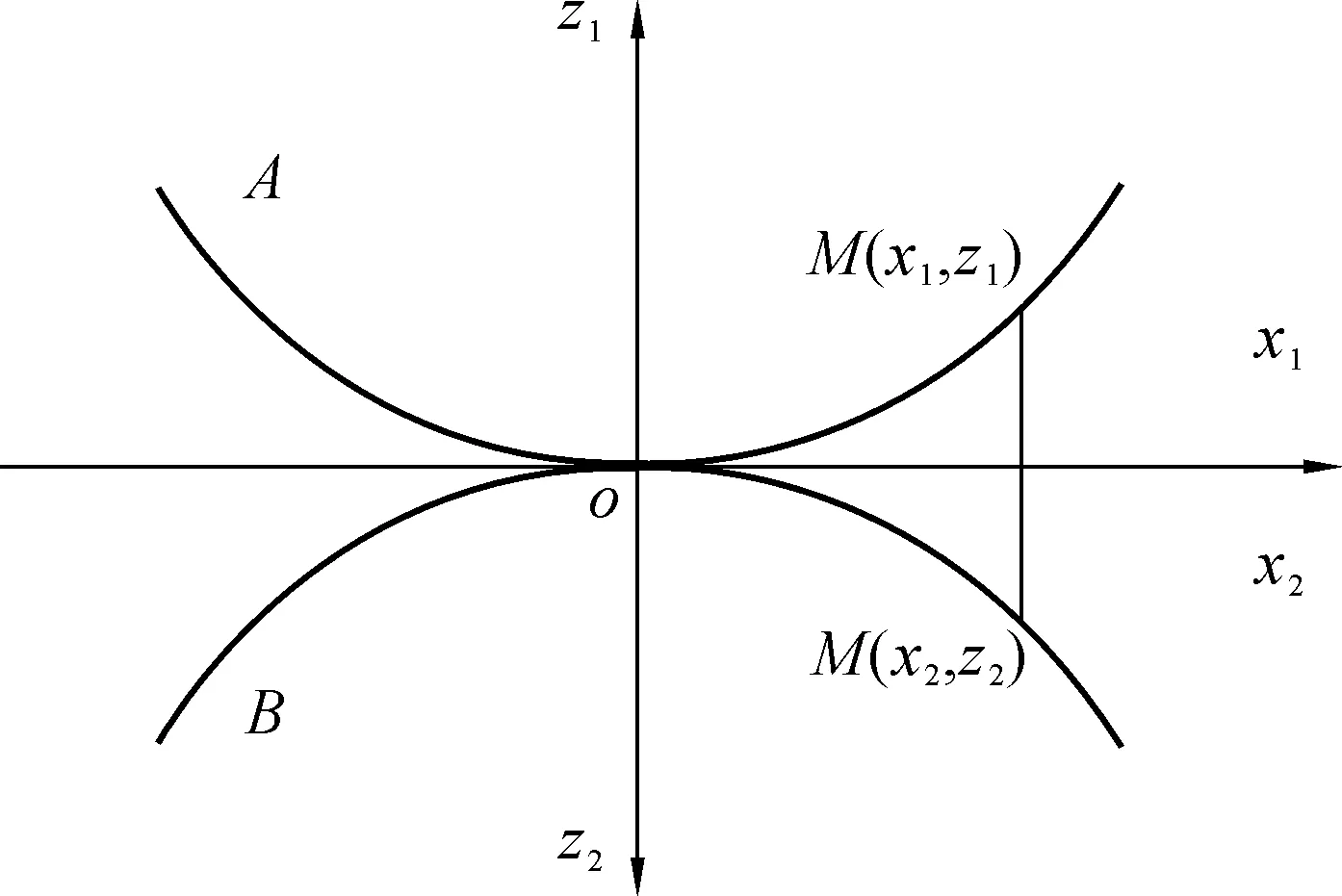
图1 两个弹性体接触示意图

ω1+ω2+z1+z2=δ(接触区域以内)，

(1)

ω1+ω2+z1+z2>δ(接触区域以外)，

(2)

式中：δ为载荷作用下两弹性体之间产生的弹性趋近量；ω1，ω2分别为弹性体A和B在接触点的弹性变形量。其中[2]，

式中：p为接触应力；υ为泊松比；E为弹性模量；s为接触应力作用面积；x′,y′为积分变量；i=1,2。

将(3)式代入(1)式中，可得变形协调方程为

(4)

接触应力还应满足平衡方程

(5)

在接触区s内p(x,y)≥0；在接触区s外p(x,y)=0。

(4)和(5)式构成了弹性接触问题的基本方程。

2 接触问题的快速直接迭代算法

在求解应力之前，要将求解区域分为若干个单元，假定每个单元结点上的应力为定值pij，则变形协调方程(4)离散后变为

(6)

(5)式离散后的表达式为

(7)

式中：α′为矩形单元面积，α′=4ab;pij≥0。

(6)式是m×n维的大型方程组，而且已经被证明是1个病态方程组[3-4]，求解起来很困难。因此需要设法将 (6)式降阶，并克服其病态。具体方法是将整个区域分为若干部分分别求解，在离散后的求解区域上，利用Gauss-Seidel迭代法对方程组进行求解，构造迭代格式如下

(8)

Pj=(pj1,pj2,…,pjn),

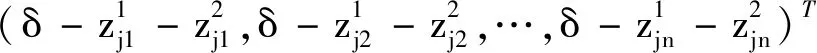
通过Gauss-Seidel迭代法求解以上方程组，虽然降低了方程组的维数，也解决了方程组的病态问题，但(8)式中每个子方程组的系数矩阵都是满元矩阵，当接触区域的网格划分比较稠密时，需要耗费较多计算时间。

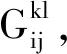
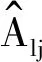
(9)

这样一来， 方程组(9)中每个等式展开后皆为方程组,且此方程组的系数矩阵都由满元矩阵变成了带宽为2β+1的稀疏带状矩阵，其中β为矩阵的半带宽，变换后的带状矩阵与前面的满元矩阵相比，运算速度要快得多，节省了大量计算时间[1]。并不是半带宽β越大，计算精度越高，当半带宽β取5～7时，即当迭代矩阵密度为满阵的15%～20%时，计算精度最高。半带宽β取值过大或者说迭代矩阵密度过高，反而不利于提高计算精度。则(9)式和离散后的 (7) 式便构成求解任意弹性表面接触问题的快速直接迭代算法。对于这种直接迭代算法的求解过程，其程序设计框图如图2所示。

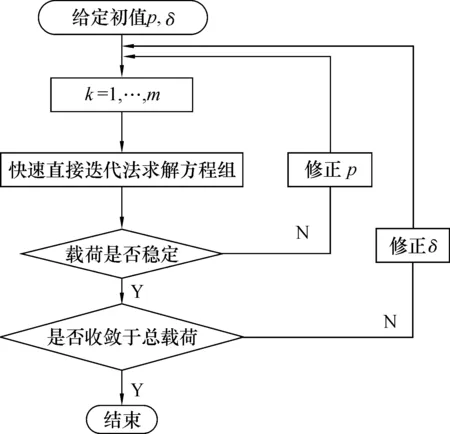
图2 程序设计框图

3 圆锥滚子接触问题的几何模型

图3给出了圆锥滚子与平面接触的几何模型。圆锥滚子被垂直于y轴的平面所截的面是大小不同的椭圆，这些截取的椭圆在接触点附近的曲率是不相同的,因此这些椭圆的接触变形和接触应力也就不同。

根据图3的几何关系，距离圆锥滚子小端Li处，圆锥体横截面的直径di和垂直于y轴的椭圆截面的长半轴ai为[6]

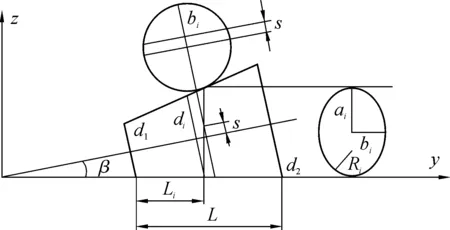
图3 圆锥滚子与平面接触的几何模型

di=(1-Li/L)d1+d2Li/L，

(10)

ai=0.5di(cosθ+sinθtan 2θ)，

(11)

式中：d1为圆锥滚子小端直径；d2为圆锥滚子大端直径；L为滚子素线有限长度；θ为圆锥滚子的半锥角。

因此,椭圆短半轴可以近似地表示为

bi=0.5di(1+sin2θ)。

(12)

通过计算可知，当θ=10°时，(12)式的相对误差小于0.2%，而实际的圆锥滚子半锥角在2°左右，因此采用(12)式可以满足计算精度要求。故椭圆截面在接触点附近的曲率半径为[7]

(13)

4 数值算例

算例中圆锥滚子的小端和大端直径分别为d1=10.0 mm，d2=12.0 mm，滚子的有限长度L=15.0 mm，半锥角θ=3°，圆锥滚子和平面的弹性模量及泊松比分别为E1=E2=210 GPa，υ1=υ2=0.3。应力迭代矩阵半带宽β=6。

图4是外加载荷为3 000 N，网格节点数为35×35时圆锥滚子与平面接触的三维应力分布图。从图4中可以看出圆锥滚子两端的应力集中效应，而且小端的接触应力要比大端的稍微大一些，其他部分应力分布比较均匀。

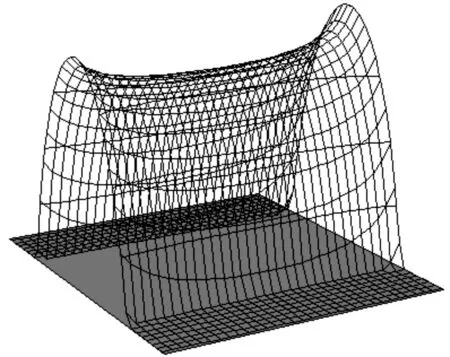
图4 圆锥滚子的三维应力分布

图5为圆锥滚子承受5种不同载荷时，滚子中心平面的接触应力分布情况。从图5中可以看出，同一曲线上滚子中心应力值右端要比左端大一些，即圆锥滚子小端的中心接触应力比大端的中心接触应力要大一些。这是因为圆锥滚子的小端曲率比大端大，应力集中明显一些。在其他的部分，接触应力分布比较均匀。

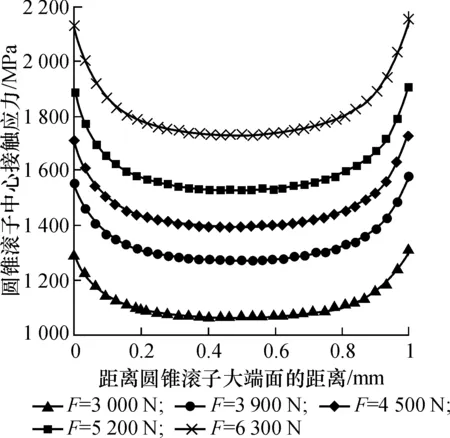
图5 不同载荷下中心平面接触应力分布曲线

5 结论

(1)给出了圆锥滚子接触问题的简化计算模型，将一种求解任意弹性表面接触问题的快速算法应用到圆锥滚子接触应力的求解中，并得到了满意的结果。

(2)计算出了不同载荷下圆锥滚子中心平面的接触应力分布。通过分析可知，在一定外载荷作用下，圆锥滚子两端存在应力集中，而且小端的接触应力比大端的接触应力要大，在沿滚子素线的其他部分，接触应力分布则比较均匀。