二阶非线性抛物型方程的周期黏性解
朴大雄,张仕林
(中国海洋大学数学科学学院,山东青岛266100)
二阶非线性抛物型方程的周期黏性解
朴大雄,张仕林
(中国海洋大学数学科学学院,山东青岛266100)
将Hamilton-Jacobi方程黏性解的比较定理推广到二阶抛物型方程中,并结合Perron方法证明了二阶非线性抛物型方程的周期黏性解的存在唯一性。
抛物型方程;周期黏性解;Perron方法
0 引言
本文研究非线性抛物型方程

的时间周期黏性解,其中Ω是RN中的1个有界开子集,H和f是连续函数,f是时间周期函数。Bostan和Namah在文献[1]中研究了Hamilton-Jacobi方程的周期和概周期黏性解的存在唯一性,Nunziante在文献[2-3]中研究了不连续时间依赖抛物型方程的黏性解的存在唯一性,但据作者所知非线性抛物型方程的周期黏性解尚没有被研究。本文将文献[1]中的黏性解的比较定理推广到了二阶抛物型方程情形,然后结合Perron方法和比较定理证明了二阶非线性抛物型方程周期黏性解的存在唯一性。关于Perron方法见文献[4-5]。
为了研究方程(1)的黏性解的存在唯一性,需要用到下面Cauchy-Dirichlet问题的一些结论。

其中,u0(x)∈C(¯Ω),Crandall,Ishii和Lions在文献[4]中研究了方程(2)的比较定理,该定理涉及到Crandall和Ishii在文献[6]中最大值原理的相关内容。本文采用记号见文献[4]。
1 一些假设和结果
为证明周期黏性解的存在唯一性,首先来看几个假设和一些结果。为此,考虑下面2个Dirichlet问题:

其中在(3)中Ω是RN中的任意开子集。
Crandall,Ishii和Lions在文献[4]中证明了这样一个定理。
定理1[4]令Oi是RNi中的一个局部紧子集,其中i=1,…,k,O=O1×…×Ok,ui∈USC(Oi),φ是O的一个邻域中的二次连续可导函数。令w(x)=u1(x1)+…+ uk(xk),(x1,…,xk)∈O,假设^x=(^x1,…,^xk)∈O是w -φ在O中的局部最大值。则对任意ε>0,存在Xi∈S(Ni)使得(Dxiφ(^x),Xi)∈¯J2,+Oiui(^xi),i=1,…,k,且所有Xi组成的斜对角线矩阵满足:

取k=2,O1=O2=Ω,u1=u,u2=-v,φ(x,y)= (α/2)|x-y|2,其中α>0,由于¯J2,-Ωv=-¯J2,+Ω(-v),则根据定理1,在u(x)-v(y)-φ(x,y)的局部最大值点(^x,^y)处,选取ε=1/α可以得到:

下面来看几个主要的假设。
如同Crandall,Ishii和Lions在文献[4]中所述,首先列出H的一个主要的单调性条件,即:对任意r≤s与Y≤X,H(x,r,p,X)≤H(x,s,p,Y),其中x∈Ω,r, s∈R,p∈RN,X,Y∈S(N),S(N)是一组N×N的对称矩阵。这样就称H是适当的。
假设存在γ>0使得

Crandall,Ishii和Lions证明了下面2个比较定理。
定理2[4]若Ω是RN中的1个有界开子集,F∈C(Ω× R×RN×S(N))是适当的且满足(5)、(6)。令u∈US C (¯Ω)(或v∈L S C(¯Ω))是F=0在Ω中的下解(或上解)并且在∂Ω上u≤v。那么在¯Ω上有u≤v成立。
定理3[4]若Ω是RN中的1个有界开子集,H∈C(¯Ω× [0,T]×R×RN×S(N))是适当的且对任意固定的t∈[0,T)和同样的函数ω满足(6)。如果u是(2)的下解, v是(2)的上解,那么在[0,T)×Ω上有u≤v。
本文推广了文献[1]中一阶Hamilton-Jacobi方程的比较定理,得到适用二阶抛物型方程的定理(见定理4)。其中需要用到下面的命题1。

对于二阶抛物型方程的比较定理,如下:
定理4 若Ω是RN中的一个有界开子集,H∈C(¯Ω× [0,T]×R×RN×S(N))是适当的且对任意固定的t∈[0,T)和同样的函数ω满足(5),(6)。设u是方程
∂tu+H(x,t,u,Du,D2u)=f(x,t),(x,t)∈Ω×(0, T);u(x,t)=0,x∈∂Ω,0≤t 的u.s.c.有界下解,v是 ∂tv+H(x,t,v,Dv,D2v)=g(x,t),(x,t)∈Ω×(0, T);v(x,t)=0,x∈∂Ω,0≤t 的l.s.c.有界上解,其中f,g∈BUC(¯Ω×[0,T])。且对任意有u(·,t)∈BUC(¯Ω),v(·,t)∈BUC(¯Ω) 有 g(·,s))+‖L∞(¯Ω)ds, 其中γ=γR0,R0=max(‖u‖L∞(¯Ω×(0,T)),‖v‖L∞(¯Ω×(0,T)))。证明 考虑函数:wα(x,y,t)=u(x,t)-v(y,t)-φ(x, y,t),其中 当其它时候,r(^t)=0。根据假设(5)可知H(x,t,z,p, X)-γ·z关于z是非减的,因此对所有的^t∈[0,T],有r(^t)≥0。注意到u(^x,^t)-v(^y,^t)=φ(^x,^y,^t),则 在r(^t)的表达式中用φ(^x,^y,^t)代替u(^x,^t)-v(^y,^t),可知r(·)是可积的,对^t∈[0,T]定义函数A(^t)=γ+r(σ)}dσ。对(7)式进行积分后得到:现在对任意^t∈[0,T]用u(^x,^t)-v(^y,^t)代替φ(^x,^y, ^t)并且令α→∞,得到 由此对所有的t∈[0,T]可以推出 定理5 若Ω是RN中的一个有界开子集,H∈C(¯Ω× R×R×RN×S(N))是适当的,T周期的且满足(5), (6)。设u是方程 ∂tu+H(x,t,u,Du,D2u)=f(x,t),(x,t)∈Ω×R; u(x,t)=0,(x,t)∈∂Ω×R的有界周期u.s.c.下解,v是∂tv+H(x,t,v,Dv,D2v)=g(x,t),(x,t)∈Ω×R; v(x,t)=0,(x,t)∈∂Ω×R的有界周期l.s.c.上解,其中f,g∈BUC(¯Ω×R)。则有 注:该定理的证明与文献[1]中的Corollary2.2类似,运用定理4可以很容易证明。 下面来看Perron方法(见文献[4-5])。首先介绍2个函数。选取O∈RN,函数 定理6 (Perron方法) 若方程(3)的比较定理成立,假设方程(3)存在1个下解u和1个上解v且对x∈∂Ω满足边界条件u*(x)=v*(x)=0。则 是方程(3)的1个解。 文献[4]中存在一个作为定理6的补充的注解。注1 假设O局部紧,G+,G-定义在O×R×RN× S(N)上并有下述性质:G+上半连续,G-下半连续, G+≤0在O的相关开子集上的经典解(逐点意义下的二阶连续可导的解)是G-≤0的解。此外,假设对O上G-≤0的解u和G+≥0的解v有u≤v。则按照Perron构造函数方法,这样的下解和上解的存在保证了存在一个函数u,它是O上G+≥0和G-≤0的唯一解。 这一部分来证明周期黏性解的存在唯一性。关于解的唯一性有下面的定理。 定理7 若Ω是RN中的1个有界开子集,H∈C(¯Ω× R×R×RN×S(N))是适当的且对t∈R满足(5),(6)。 设u是方程 ∂tu+H(x,t,u,Du,D2u)=f(x,t),(x,t)∈Ω×R; u(x,t)=0,(x,t)∈∂Ω×R的有界u.s.c.下解,v是∂tv+H(x,t,v,Dv,D2v)=g(x,t),(x,t)∈Ω×R; v(x,t)=0,(x,t)∈∂Ω×R的有界l.s.c.上解,其中f, g∈BUC(¯Ω×R)。则对所有的t∈R有 证明 取t0,t∈R,t0≤t,对所有的x∈¯Ω应用定理4得到 关于解的存在性有下面的定理。 定理8 若Ω是RN中的一个有界开子集,H∈C(¯Ω× R×RN×S(N))是适当的且满足(5),(6)。假设f是T周期的且存在M>0使得对任意x∈¯Ω,t∈[0,T]有H(x,-M,0,0)≤f(t)≤H(x,M,0,0)成立,则方程(1)在¯Ω×R上存在1个时间周期黏性解。 证明 首先考虑这样一个问题 由于Ω是RN中的有界开子集,可知u0∈BUC(¯Ω)。由H(x,-M,0,0)≤f(t)≤H(x,M,0,0)推出∓M分别是(8)的下(上)解,通过定理3与注1中的Perron方法可知方程(8)存在唯一黏性解u∈C(¯Ω×[0,+∞)),且对(x,t)∈¯Ω×[0,T),-M≤u(x,t)≤M,对n≥0,令un(x,t)=u(x,t+nT)。对任意(x,t)∈¯Ω×[0,+∞),考虑v(x,t)=u(x,t+T),由于f是T周期的,可以推出v是方程∂tv+H(x,v,Dv,D2v)=f(t),(x,t)∈Ω×[0,+∞)的黏性解。运用定理4,有 特别地,令t=s+nT,s∈[0,T],则有‖un+1(·,s)-un(·,s)‖L∞(¯Ω)≤e-nTγ·2M,因此存在w∈C(¯Ω×R)是T周期的使得在¯Ω×[0,T]上un一致收敛于w。通过连续黏性解的稳定性结果知道w是方程(1)在¯Ω× [0,T)上的黏性解,由w的周期性知道,w是方程(1)在¯Ω×R上的周期黏性解,且由un∈BUC(¯Ω×[0,T],∀n)可知w∈BUC(¯Ω×R)。 [1] Bostan M,Namah G.Time periodic viscosity solutions of Hamil-ton-Jacobi equations[J].Commun Pure Appl Anal,2007,6:389-410. [2] Nunziante D.Uniqueness of viscosity solutions of fully nonlinear second-order parabolic equations with discontinuous time-dependence[J].Differential Integral Equations,1990,3:77-91. [3] Nunziante D.Existence and uniqueness of unbounded viscosity solutions of parabolic equations with discontinuous time-dependence [J].Nonlinear Analysis TMA,1992,18:1033-1062. [4] Crandall M G,Ishii H,Lions P L.User’s guide to viscosity solutions of second order partial differential equations[J].Bull Amer Math Sco,1992,27:1-67. [5] Ishii H.Perron’s method for Hamilton-Jacobi equations[J].Duke Math J,1987,55:369-384. [6] Crandall M G,Ishii H.The maximum principle for semicontinuous functions[J].Differential Integral Equations,1990,3:1001-1014. Abstract: In this paper we generalize the comparison theorems for the solutions of Hamilton-Jacobi equations to second order parabolic equations,then by using Perron’s method we prove the existence and uniqueness of time periodic viscosity solutions of second order nonlinear parabolic equations under usual hypotheses. Key words: parabolic equations;time periodic viscosity solutions;Perron’s method AMS Subject Classifications: 35BW,35D05,35K55 责任编辑 朱宝象 Periodic Viscosity Solutions of Second Order Nonlinear Parabolic Equations PIAO Da-Xiong,ZHAN G Shi-Lin O175.26 A 1672-5174(2011)04-131-04 国家自然科学基金项目(10371010)资助 2009-09-17; 2010-04-11 朴大雄(1962-),男,教授,博导。E-mail:dxpiao@ouc.edu.cn


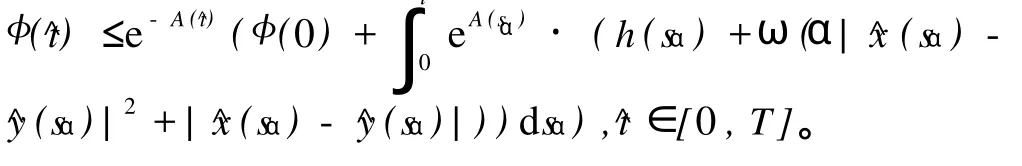





2 黏性解的存在唯一性
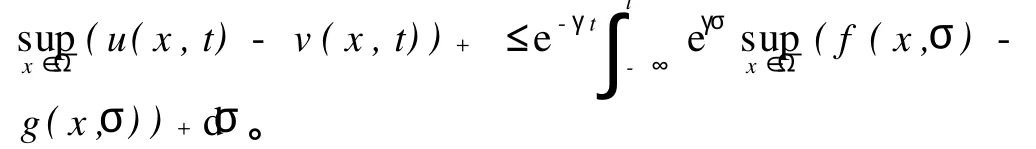
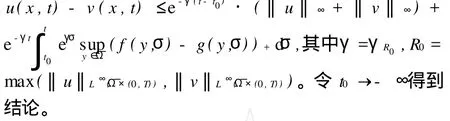
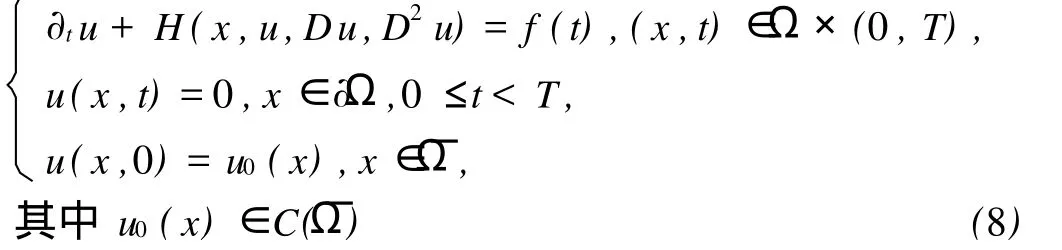
(School of Mathematical Science,Ocean University of China,Qingdao 266100,China)

