有限维欧氏空间上线性映射的广义逆＊

钱 莉

(湖州师范学院理学院,浙江湖州 313000)

有限维欧氏空间上线性映射的广义逆＊

钱 莉

(湖州师范学院理学院,浙江湖州 313000)

线性映射和广义逆是高等代数很重要的研究对象.线性变换的广义逆被普遍研究,而线性映射的广义逆性质研究地很少.应用共轭映射的性质,给出了欧式空间商线性映射的广义逆的定义,并研究它的若干性质。这些性质对学生的学习有一定的帮助作用.

线性映射;广义逆;欧氏空间

MSC 2000:17B40

线性变换的广义逆矩阵是一种非常有用的数学工具,它在线性代数、数理统计、微分方程、泛函分析、物理学、测量学等方面都有着广泛的应用,而且在实际的应用中线性映射比线性变换更广泛.根据矩阵与映射的相关性,我们也可探究线性映射的共轭与广义逆,以便更好地学习线性映射的运算.本文利用线性变换的共轭变换与广义逆理论,给出欧氏空间线性映射共轭与广义逆的定义,并研究其相关性质.

1 线性映射的共轭

定义1[1]V是n维欧氏空间,W是m维欧氏空间,如果存在映射V→W的映射σ,使得它满足以下条件:

(1) 对 V 中任何向量α和β,σ(α+β)=σ(α)+σ(β);

(2) 对任何数 k,σ(kα)=kσ(α),则称σ是线性映射.

定义2[2]A为实m×n阶矩阵,若存在n×m阶实矩阵B使得:①AB为实对称阵;②BA为实对称阵;③ABA=A;④BAB=B,则称B为A的广义逆矩阵.

下面给出线性映射的共轭映射的定义.

定义3 设σ是V→W的线性映射,如果存在W →V的线性映射σ＊,使得

∀α∈V,β∈W.则称σ＊为σ的共轭映射,显然当V=W 且σ＊=σ时,σ就是对称变换.

给定一个线性映射,它的共轭映射是存在且唯一的.

命题1 设σ是V →W的线性映射,存在W →V的线性映射σ＊,使得

且σ＊唯一.

证明 存在性:设 f是V →R的任何一个线性函数,则存在唯一的 v∈V,使得

事实上 ,在 V 中取{ε1,ε2,…,εn} 是标准正交基 ,取 v=f(ε1)ε1+ …+f(εn)εn,则有(α,v)=k1f(ε1)+…+knf(εn)=f(k1ε1)+…+f(knεn)=f(α).现在构造σ＊∶∀β∈W,定义

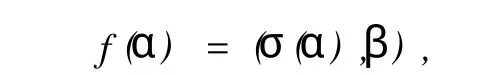
则根据前面叙述,存在唯一的 v∈V,使得

定义σ＊∶V →W,σ＊(β)=v,所以

故σ＊存在.

命题2 设σ是V →W 的线性映射,则有(σ＊)＊=σ.

证明 由命题1,得到存在W →V的线性映射σ＊,使得

又由于

根据共轭映射的定义,

所以由前面的论述,可以得到:

故由α,β的任意性得:

命题3 设σ是V →W 的线性映射,τ是W →V的线性映射,则有(στ)＊=τ＊σ＊.

证明 根据条件στ是W中的线性变换,由共轭映射的存在性,可知存在V→W的线性映射τ＊和W→V的线性映射σ＊,使得

同时τ＊σ＊是W 中的线性变换,所以有:

根据共轭变换的定义,可知τ＊σ＊是στ的共轭变换,即有:

2 线性映射的广义逆

线性变换的广义逆已经被充分讨论.在此基础上,我们给出欧氏空间上线性映射广义逆的定义,并初步讨论其性质.

定义4 设V、W是两个欧氏空间,σ是V →W的线性映射,τ是W →V的线性映射,如果有:①στ为实对称变换;②τσ为实对称变换;③στσ=σ;④τστ=τ,则称τ为σ的广义逆,记作τ=σ+.

命题4 σ是V →W的线性映射,若σ可逆,则它的广义逆就是它的普通逆.

命题5 设σ是V→W的线性映射,若存在W →V的线性映射τ,且τ为σ的广义逆,则τ=σ+是唯一的.

证明 设τ1、τ2都是σ的广义逆,即τ1、τ2满足定义中的 ①～ ④,则

因为τ1σ和τ2σ是对称变换,所以

且στ2和στ1是对称变换,所以

综上所述τ=σ+是唯一的.

为了进一步研究广义逆的性质,我们需要下列引理:

引理1[3]设 T是n维欧氏空间V的线性变换,T＊是V的共轭变换,则 T＊可逆的充分必要条件是T 可逆,且(T＊)-1=(T-1)＊.

引理2[3]设α1,…,αn是n维空间V的一基,V的线性变换 T可逆的充要条件是 Tα1,…,Tαn也是V的一组基.

命题6 V是n维线性空间,W是m维线性空间,若σ是V→W的线性单射,则σ＊σ是可逆的.

证明 由于线性映射的共轭映射存在且唯一,σ＊是W →V的线性映射,显然σ＊σ是V上的线性变换,设{ε1,…,εn}是 n维线性空间V中的标准正交基,令

根据共轭映射的定义,则有:

令 k1σ＊σε1+ …+knσ＊σεn=0,则(σα,σα)=(α,σ＊σα)=0,所以σα =0. 但由于σ是单射 ,所以α =k1ε1+…+knεn=0,所以k1=…=kn=0.即σ＊σε1,…,σ＊σεn线性无关,是V的一组基,由引理2得,是σ＊σ可逆变换.

命题7 设σ:V →W 的线性单射,则τ=(σ＊σ)-1σ＊就是线性映射σ的广义逆.

证明 由性质3得(σ＊σ)-1有意义,根据条件有:

根据对称变换的定义,单位变换是对称变换,可知στ也是对称变换.根据条件有:

所以τσ也是对称变换.因为

故τ满足线性映射广义逆的四个条件,所以τ是线性映射σ的广义逆.

推论1 设σ:V →W的线性单射,如果存在W →V的线性映射τ,且τ是线性映射σ的广义逆,则τσ和στ是恒等变换.

证明 根据线性映射广义逆的唯一性,如果存在线性映射σ的广义逆τ,则必有τ=(σ＊σ)-1σ＊,故

所以τσ和στ是恒等变换.

命题8 设σ:V →W的线性映射,如果存在W →V的线性映射τ=σ+,则

证明 要证(σ+)＊是σ＊的广义逆,则必须满足线性映射的广义逆的四个条件.

先证(σ+)＊σ＊,σ＊(σ+)＊是对称变换.

因为存在W →V的线性映射τ=σ+,(σ+)＊σ＊是V中的线性变换,又根据命题3可知:

易知(σ+)＊σ＊是σσ+的共轭变换,又由于σ+是σ的广义逆,则σσ+是对称变换,即

所以有:

故(σ+)＊σ＊也是对称变换,同理可得σ＊(σ+)＊也是对称变换.

再证(σ+)＊σ＊(σ+)＊=(σ+)＊,σ＊(σ+)＊σ＊=σ＊.根据命题 3 可知:

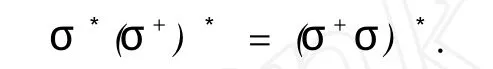
又因为

而σ+是σ的广义逆,则

因此得:

同理可证

所以满足线性映射的广义逆的四个条件,则(σ+)＊是σ＊的广义逆,即有:

与矩阵的广义逆一样,线性映射的广义逆也应该有着十分广泛的应用.

致谢:在此感谢湖州师范学院理学院刘东副教授对本文的指导.

[1]王萼芳,石生明.高等代数(第3版)[M].北京:高等教育出版社,2003:178.

[2]贾正华.广义逆矩阵及其性质 [J].巢湖学院学报,2005,7(3):38～39.

[3]杨子胥.高等代数精选题解 [M].北京:高等教育出版社,2008:103.

Abstract:Linearmapsand generalized inversesare very important objects in Higher A lgebra.Some p roperties of generalized inverses of linear translations are studied in many papers.However,there are few researches about generalized inversesof linearmaps.With the conjugation of matrices,we give the definition of the generalized inverse of a linear mapping in Euclidean Space and study its some p roperties.They can help for study and applications of matrix theories.

Key words:linear mapping;generalized inverse;Euclidean Space

MSC 2000:17B40

Generalized Inverse of L inear Mapping in Euclidean Space

Q IAN Li
(Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

O152.5

A

1009-1734(2011)01-0054-04

2010-09-25;

2010-11-20

浙江省新世纪教改项目(yb07109,ZC09063);湖州师范学院教改重点项目(08JY006).

钱莉,湖州师范学院理学院2007级本科生,从事线性映射研究.