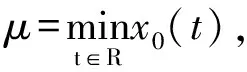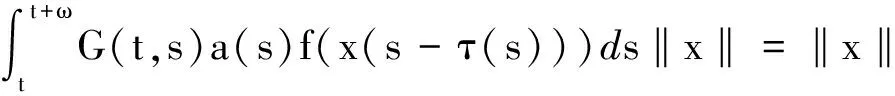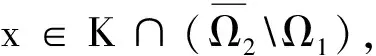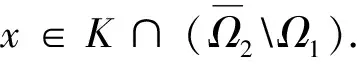一阶时滞泛函微分方程的正周期解
金爱云,张国伟
(1.郑州航空工业管理学院 数理系, 河南 郑州 450015;2.东北大学 数学系,辽宁 沈阳 110004)
泛函微分方程周期正解这一课题引起了人们的广泛关注,有不少作者利用不同的周期模型讨论了该问题[1-2],文献[3]中讨论了一般泛函微分方程u′(t)=-a(t)u(t)-g(t,u(t-τ(t)))周期解的存在性.
这里,我们考虑泛函微分方程
x′(t)=-a(t)f(x(t-τ(t)))x(t)+g(t,x(t-τ(t))),
(1)
的周期正解存在性问题.其中,a(t)∈C(R,[0,∞)),f∈C([0,∞),(0,∞)),g∈C(R×[0,∞),[0,∞)),τ(t)∈C(R,R),并且a(t),τ(t)都是ω-周期泛函,g(t,x)关于t为ω-周期泛函,ω>0为一个常数,f(x)为有界泛函.
本文利用锥中的不动点定理来处理方程(1)的周期正解的存在性问题,即找到一个泛函及一个适当的算子满足, 推广了文献[3]中相应的结论.
1 准备工作
设X是实Banch空间,K是X的一个非空闭子集,K为一个锥.即
1)αu+βv∈K,∀u,v∈K且α,β≥0,
2)u,-u∈K,也即u=0.
假设(P)a(t)∈C(R(0,∞)),τ(t)∈C(R,R),g∈C(R×[0,∞),[0,∞)),f∈C([0,∞),(0,∞)), 并且a(t),τ(t),g(t,x)都是ω-周期泛函,ω>0为一个常数,f(x)为有界泛函.
如果u(t)∈C([0,ω],[0,+∞)), 并且u(t)满足方程(1), 则称u(t)为方程(1)的解.如果在(0,ω)上u(t)>0, 则称u(t)为方程(1)的正解.
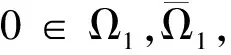
1) ‖Φx‖≤‖x‖,x∈K∩∂Ω1,
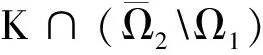
定理1 假设(P)成立, 方程(1)若满足下列条件:


则至少有1个ω-周期正解.
首先,我们指出方程(1)的ω-周期解即为积分方程
(2)
的解. 其中
(3)
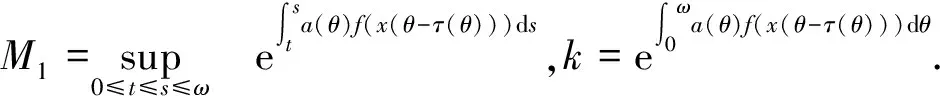
则X在范数‖C‖下是Banach空间. 定义X上的算子:
x=Φx.
(4)
其中
(5)
令K={x∈X:x(t)≥0,且x(t)≥σ‖x‖,t∈[0,ω]},0<σ=A/B<1,且

易证K是X中的一个锥.
引理2 假设(P)成立, 则Φ(K)⊂K.
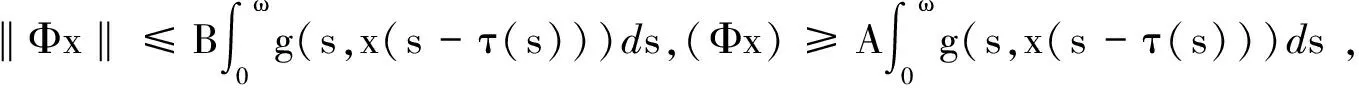
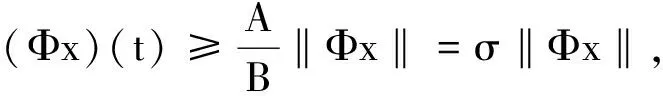

2 主要结论的证明
下面我们证明定理1在(1)或(2)成立下的结论.
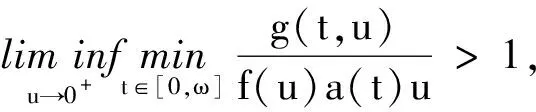
g(t,u)≥f(u)a(t)u,0≤u≤r,
(6)
因此, 如果x∈K,且‖x‖=r,则x(t)≥σr.
令ψ≡1,t∈R,我们证明
x≠Φx+λψ,x∈K∩∂Ω1,λ>0,
(7)
其中,Ω1={u∈X:‖u‖ 如若不然,存在x0∈K∩∂Ω1,λ0>0, 使得x0=Φx0+λ0ψ, 令R=r1/σ, 于是有 u(t)≥σ‖u‖=σR=r1,u∈K∩∂Ω2, (8) 其中,Ω2={u∈X:‖u‖ g(t,u)≤f(u)a(t)u,0≤u≤r, (9) 因此, 如果x∈K,且‖x‖=r,则x(t)≥σr.于是, 对,x∈K,‖x‖=r,有 也即‖Φx‖≤‖x‖,其中x∈K∩∂Ω1,Ω1={u∈X:‖u‖ u(t)≥σ‖u‖=σR=r1,u∈K∩∂Ω2, (10) 其中,Ω2={u∈X:‖u‖ 令ψ≡1,t∈R,证明 x≠Φx+λψ,x∈K∩∂Ω2,λ>0 (11) 如若不然,存在,x0∈K∩ ∂Ω2,λ0>0使得x0=Φx0+λ0ψ. 参考文献: [1] 彭世国,朱思铭.无穷时滞泛函微分方程的正周期解[J].数学年刊,2004(3):285-292. [2] Liu X,Li W.Existence and uniqueness of positive periodic solutions of functional differential equations[J].J Math Anal Appl, 2004(293):28-39. [3] Wan A, Jiang D ,Xu X. A new existence theory for positive periodic to functional differential equations [J].Comput Math Appl,2004(47):1257-1262. [4] K Deimling.Nonlinear Functional Analysis[M].New York:Springer-Verlag, 1985. [5] K Lan, K Jeffry,J R L Webb.Positive solutions of semilinear differential equations with singularities[J].J Differential Equations,1998(148): 407-421.