一类厄尔尼诺-南方涛动耦合振子动力学模型的震荡近似解*

林万涛 林一骅 石兰芳 莫嘉琪

1)(中国科学院大气物理研究所,大气科学和地球流体力学数值模拟国家重点实验室,北京 100029)

2)(南京信息工程大学数学与统计学院,南京 210044)

3)(安徽师范大学数学计算机科学学院,芜湖 241003)

(2013年2月14日收到;2013年3月22日收到修改稿)

1 引言

厄尔尼诺和南方涛动(ENSO)分别是发生在热带大气和海洋中的异常事件,它严重地影响全球各地和区预气防为候当和前生学态术等界方所面关的注变化[1-,9对].它海的洋规和律大的气研之究间的交互作用影响着气候的波动,这对种交互作用的研究已经集中在厄尔尼诺-南方涛动现象上,它每隔3到4年周期地出现,并主要发生在热带太平洋区域.厄尔尼诺和南方涛动的振荡性态是海-气流动的正负两种反馈的结果,这两种反馈决定了海表温度(SST)的变化,并与南方涛动流动强度有关,导致了弱信风沿着赤道行进.弱信风驱动着海洋流动变化,加强了SST的异常.海洋-大气的正反馈与耦需合研的究不东、稳定西性太平导致洋了振子赤模道太型平的异洋温常度关变系.化许,因多此学者已使用不同的方法对ENSO局部和整体的性态做了多方位的讨论[1-6].对于复杂的全球海-气耦合模型,通过简化的海-气非线性相互作用物理过程得到的振子概念模型能更容易描述海-气耦合过程的本质和物理机理,从而能描述ENSO的某些重要物理现象.因此许多学者提出了研究ENSO的各种振子形式的动力系统模型[7-12],如“时滞振子”,“平流-反射振子”,“西太平洋振子”,“充电-放电振子”等理论的研究.本文研究一类ENSO海-气耦合振子震动动力学模型[11].近来,许多学者研究了非线性奇摄动问题,一些近似方法被优化,包括边界层法、平均化法、匹配近似展开方法和多重尺度法等[13-17].作者等也利用摄动理论等方法研究了一类非线性问题[18-30].本文是利用摄动理论来讨论一类ENSO海-气耦合振子.

2 ENSO耦合振子模型

考虑如下ENSO耦合振子动力学模型[7-9]：

其中T表示赤道东太平洋的SST距平,h表示赤道西太平洋的温跃层厚度距平,C,D,E,Rh表示正参数,它们的详细定义和物理意义参见文献[7,8],ε为小的正参数.本文是求ENSO耦合振子动力学模型(1),(2)的震荡近似解.

首先对方程(1)两边进行d/d t+Rh运算,考虑到(2)式,当C＞Rh,DE＞CRh时,可得

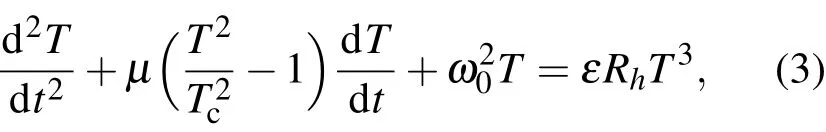
其中

由(3)式,对应的方程：

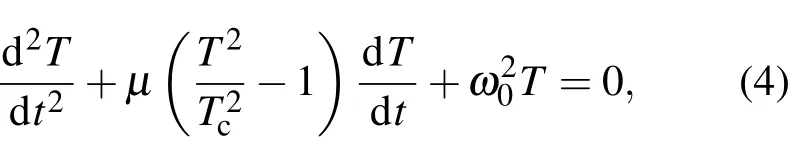
这就是van der Pol方程.由van der Pol方程的性态知,方程(4)当T＜Tc为负阻尼方程,当T＞Tc为正阻尼方程.此外,方程(4)可改写为如下等价的平面系统：

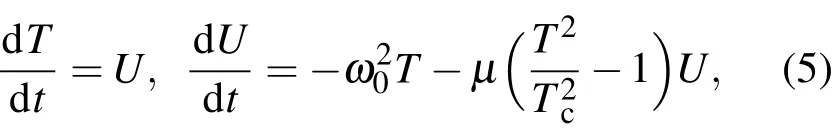
不难看出,系统(5)有一个平衡态(T∗,U∗)=(0,0).其对应的特征方程和特征根为

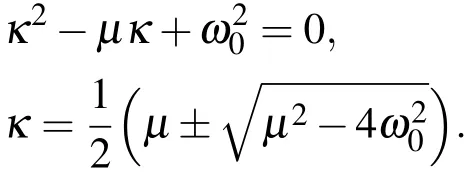
由此可知[11],当µ2＜4ω02时,即在弱阻尼的情况下,平衡态(T∗,U∗)=(0,0)是一个不平衡的焦点;当µ2＞4ω02时,即在强阻尼的情况下,平衡态(T∗,U∗)=(0,0)是一个不平衡的结点.因此,这时海-气耦合振子当气候稍有偏离平衡态时,将会处于不稳定状态,并且还不难看出,当µ=0(无阻尼的情形),van der Pol方程(3)是一个Hamilton系统.当ε很小时,在无阻尼情形时,海表温度距将做周期振荡.当µ/=0的情形,在弱阻尼的条件下,存在两个平衡态：一个平衡态就是(T∗,U∗)=(0,0),便是不稳定的焦点;另一个平衡态就是在相平面(T,U)上,是一个闭合的极限环.它是van der Pol方程在弱阻尼的情况下求得的孤立波周期解(周期吸引子),即当运动脱离平衡态后,有可能进入一个周期的运动,其周期为2π/ω0的气候震荡状态.

3 ENSO模型的振荡近似解

对于小的参数ε,在弱阻尼的条件下,我们用Krylov-Boglinbov方法来求弱阻尼方程(3)振荡近似解.方程(3)可改写为

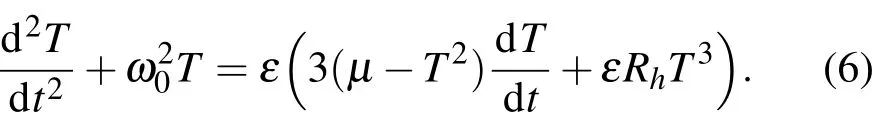
当参数ε=0时,方程(6)的解为

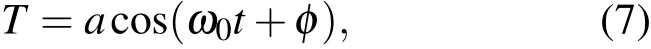
其中a,φ为常数.对于ε/=0时,我们采用广义的“常数变易法”.将方程的解看作仍由方程(6)的形式,但a,φ为时间t的函数,且满足条件

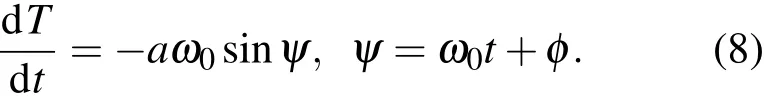
现对(7)式求导

比较(8),(9)式得

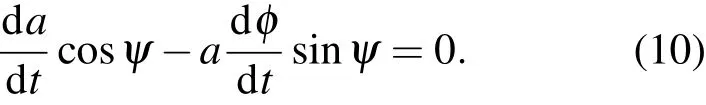
再对(8)式求导,有

将上式代入方程(6),并考虑到(7)式,得

从(10),(11)式解出 d a/d t,dφ/d t,得到

为了解(12),(13)式,注意到这些方程右边关于变量ψ是周期函数,所以有

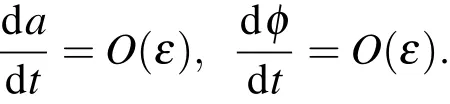
因为ε是小量,a和φ是时间t的慢变函数,所以在时间周期2π/ω0区间内它们的变化是很小的.把这些方程右边的a和φ当作常数,在一个周期[t,t+(2π/ω0)]上求 (12),(13)式的平均值,得到

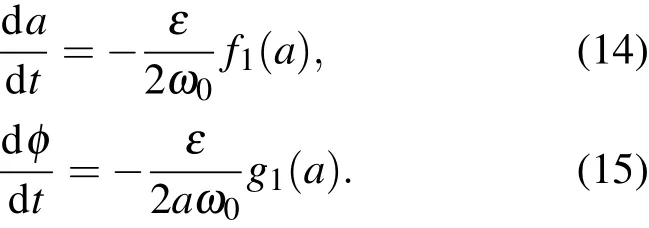
其中

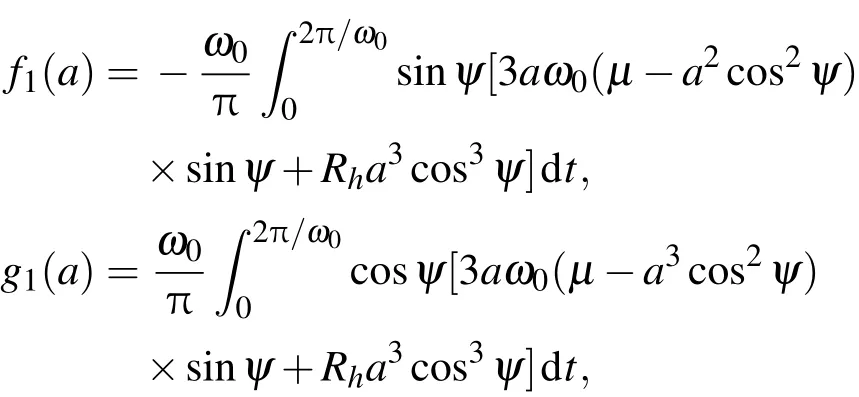
即

于是由(14)—(16)式知

积分(17),(18)式,得到

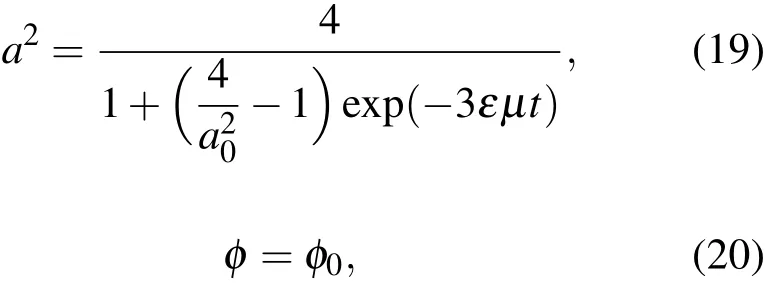
其中a0和φ0为常数.将(19),(20)式代入(7)式,我们便得到弱阻尼van der Pol方程(4)的震荡近似解：

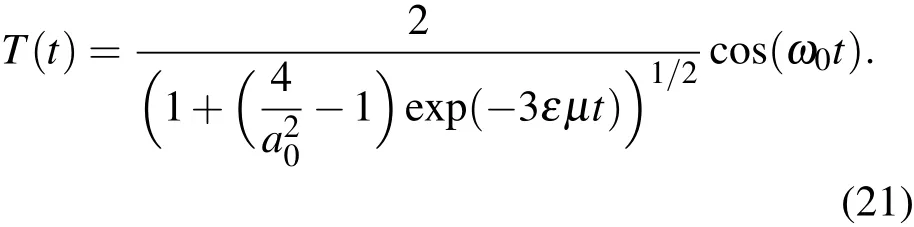
再将(21)式代入方程(2),得

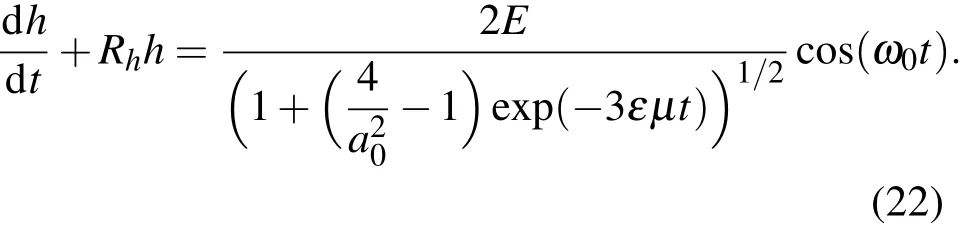
由方程(22),有解

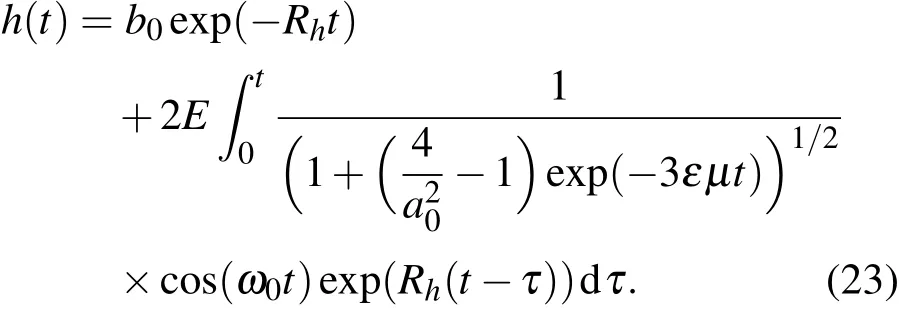
故(21),(23)式便是ENSO耦合振子动力学模型(1),(2)的震荡近似解.用同样的方法,还可继续得到ENSO耦合振子动力学模型更高次的震荡近似解.

4 举例

现举例说明ENSO耦合振子动力学模型解的震荡性态.为了方便起见,我们假设如下无量纲方程：

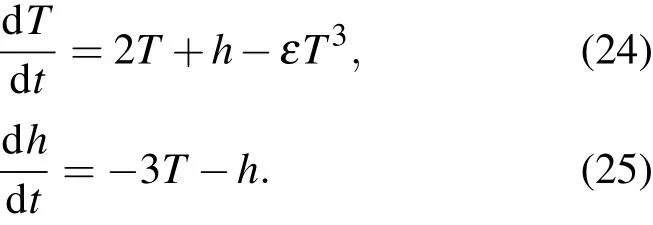
比较模型(1),(2)知C=2,D=Rh=1,E=3,µ=1,ω0=1.现求模型(24),(25)式的近似解.由(24),(25)式,对应于方程(5)为

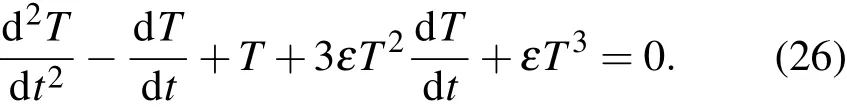
由(8)式,设方程(26)的解为

由(14),(15)式

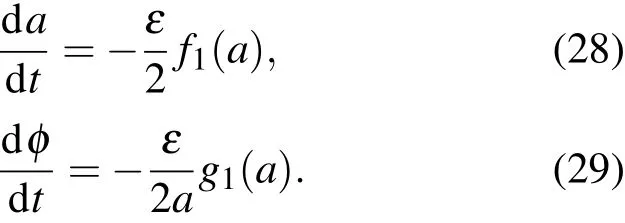
其中

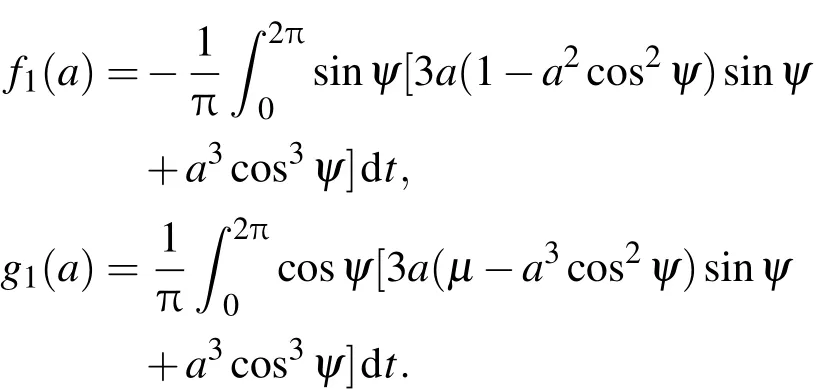
即有

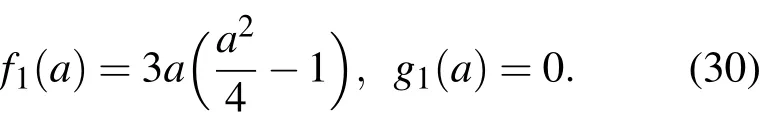
于是由(14)—(16)式知

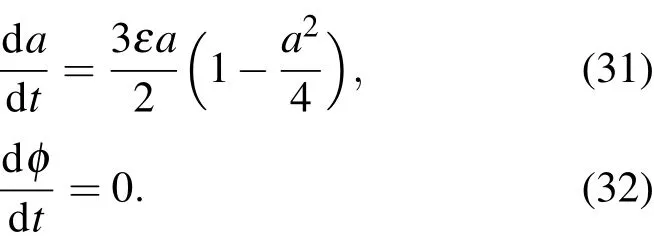
积分(31),(32)式,得到

其中a0和φ0为常数.将(33),(34)式代入(27)式,我们便得到方程(26)的震荡近似解：

将(35)式代入方程(25),得

由方程(36),有解

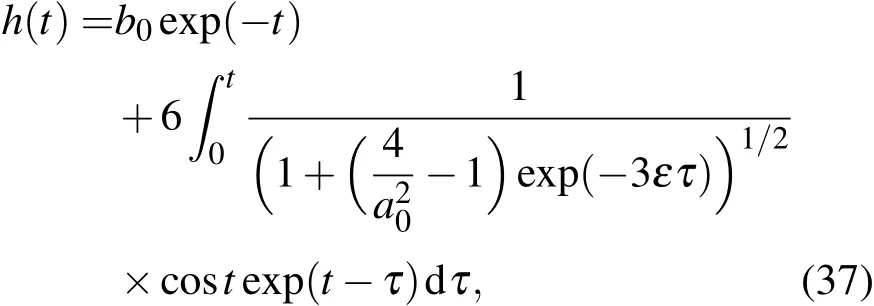
其中a0,b0为常数.故(35),(37)式便是ENSO耦合振子动力学模型(24),(25)的震荡近似解.现设T(0)=h(0)=1,这时由解(35),(37)式得

由方程(36),有解

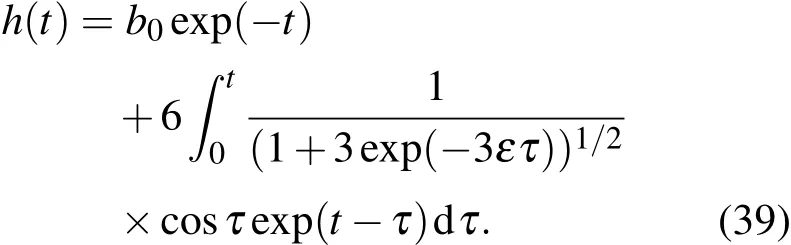
当在初始条件T(0)=h(0)=1,ε=0.5下,震荡近似解(38),(39)曲线图见图1和图2所示.由图1和图2可以看出,ENSO耦合振子动力学模型(24),(25)具有震荡型的近似解.

5 结论

由于大气物理中的复杂性,需要建立它的基本模型系统的方程,并去求解它.参数变值法和平均法是一个简单而有效的方法.它类同于变系数非齐次常微分方程的常数变易法,但比常数变易法更深入,加上了取变量函数平均值的过程,以达到求得近似解的目的.这种方法对消去解的长期项的有界解用相应的近似解来替代很有效,同样,这种近似解保留了解析表达式的特点,以便可以继续对它使用解析运算.因此可以利用它对模型的相应的定性性质做进一步的探讨,这对进一步了解和预测模型的有关性质更为方便和实用,特别是对大气物理方面的气象预报等的描述.

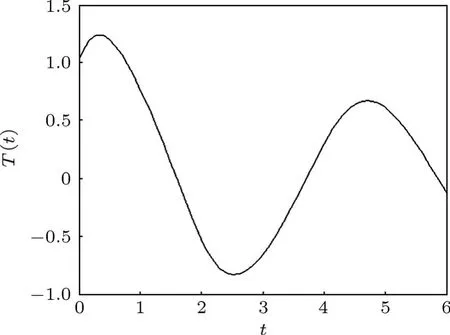
图1 ENSO耦合振子海表温度T(t)近似震荡曲线图

图2 ENSO耦合振子温跃层厚度h(t)近似震荡曲线图

[1]Feng GL,Dong WJ,Jia X J,Cao H X 2002 Acta Phys.Sin.51 1181(in Chinese)[封国林,董文杰,贾晓静,曹鸿兴2002物理学报51 1181]

[2]Guan X P,He Y H,Fan Z P 2003 Acta Phys.Sin.52 276(in Chinese)[关新平,何宴辉,范正平2003物理学报52 276]

[3]Li CG 2003 Acta Phys.Sin.52 2114(in Chinese)[李春贵2003物理学报52 2114]

[4]Li Z,Han CZ 2002 Chin.Phys.11 9

[5]Lin J,Xu Y S2003 Chin.Phys.12 1049

[6]Hu Y Q 2002 Introductory to Atmospheric Thermodynamics and Dynamics—Linear and Nonlinear Thermodynamicsof the Atmospheric Non-equilibrium State(Beijng：Geology Pub.)(in Chinese)[胡隐樵2002大气热力动力学导论——大气非平衡态线性和非线性热力学(北京：地质出版社)]

[7]Jin FF 1997 J.Armos.Sci.54 811

[8]Jin FF 1997 J.Armos.Sci.54 830

[9]Wang C 2001 1999 J.Adv.Atmosph.Sci.18 674

[10]Feng G L,Dong W J 2005 Acta Meteo.Sin.63 864(in Chinese)[封国林,董文杰2005气象学报63 864]

[11]Zhao Q,Liu SK,Liu SD 2012 Acta Phys.Sin.61 220201(in Chinese)[赵强,刘式适,刘式达2012物理学报61 220201]

[12]Liu S K,Liu S D 2012 Nonlinear Equations in Physics(Beijing：Peking University Press)(in Chinese)[刘式适,刘式达 2012物理学中的非线性方程(北京：北京大学出版社)]

[13]de Jager E M,Jiang F R 1996 The Theory of Singular Perturbation(Amsterdam：North-Holland Publishing Co.)

[14]Barbu L,Morosanu G 2007 Singularly Perturbed Boundary-Value Problems(Basel：Birkhauserm Verlag AG)

[15]Ramos M 2009 J.Math.Anal.Appl.352 246

[16]D’Aprile T,Pistoia A 2010 J.Diff.Eqs.248 556

[17]Faye L,Frenod E,Seck D 2011 Discrete Contin.Dyn.Sys.29 1001

[18]Lin WT,Ji ZZ,Wang B 2002 Prog.Nat.Sci.12 102(in Chinese)[林万涛,季仲贞,王斌2002自然科学进展12 102]

[19]Lin W T,Mo JQ 2004 Chin.Sci.Bull.48(suppl II)5

[20]Lin W T,Lin Y H,Mo JQ 2012 Chin.Phys.B 21 010204

[21]Shi L F,Ouyang C,Chen L H,Mo J Q 2012 Acta Phys.Sin.61 050203(in Chinese)[石兰芳,欧阳成,陈丽华,莫嘉琪2012物理学报61 050203]

[22]Shi L F,Lin W T,Lin Y H,Mo JQ 2013 Acta Phys.Sin.62 010201(in Chinese)石兰芳,林万涛,林一骅,莫嘉琪2013物理学报62 010201]

[23]Mo JQ,Lin Y H,Lin W T,Chen L H 2012 Chin.Geog.Sci.22 42

[24]Mo JQ 2009 Sciencein China G 39 568

[25]Mo JQ,Lin Y H,Lin WT 2010 Acta Phys.Sin.59 6701(in Chinese)[莫嘉琪,林一骅,林万涛2010物理学报59 6701]

[26]Mo JQ,Lin W T,Lin Y H 2011 Acta Phys.Sin.60 080202(in Chinese)[莫嘉琪,林万涛,林一骅2011物理学报60 080202]

[27]Mo JQ 2011 Acta Phys.Sin.60 090203(in Chinese)[莫嘉琪2011物理学报60 090203]

[28]Mo JQ 2010 Commun.Theor.Phys.53 440

[29]Mo JQ,Lin Y H,Lin WT 2010 Chin.Phys.B 19 030202

[30]Mo JQ,Lin WT,Lin Y H 2011 Chin.Phys.B 20 070205