关于条件概率及其应用教学方法的研究*

宋明珠

(铜陵学院数学与计算机系，安徽铜陵244000)

条件概率是《概率论与数理统计》课程中的一个重难点，由条件概率推导出的全概率公式和贝叶斯公式在实际生活中有着广泛的应用，同时也是考研的重点。但在多年的教学过程中发现:大多数学生对这两个公式掌握不够准确，在遇到实际问题时无从下手。案例教学是以学生为中心，学生和教师之间进行交互式探索的教学方法。为了避免直接抽象地给出公式给学生带来的困惑，采用案例教学，通过对实际案例分析导入新课，在分析的过程中既要发挥教师的引导、指导作用，又要发挥学生的主动性和积极性，激发学生的学习兴趣，使学生轻松掌握条件概率、全概率公式和贝叶斯公式以及其适用范围，从而提高教学效果。

1 条件概率的教学方法

为了让学生轻松掌握条件概率的定义以及它的实际意义，从学生感兴趣的实际问题出发，引出条件概率的定义。

引例1 掷一枚骰子，观察其点数，设事件A为“出现的点数为奇数”，事件B为“出现的点数不超过3”，求在事件A已经发生的条件下事件B的发生概率。

解 样本空间为Ω={1，2，3，4，5，6}，且每个可能的事件都等可能发生，故属于古典概型，由题意可知A={1，3，5}，B={1，2，3}，所以 P(B)

记P(B|A)表示在事件A已经发生的条件下事件B的发生概率，因为事件A已经发生，则此时试验的样本空间缩减为A={1，3，5}，此时B事件包含两个基本事件{1}，{3}，所以P(B|A)

显然有P(B)≠P(B|A)，即概率和条件概率是有区别的，为此引入条件概率的定义。

定义1［3］设A，B为随机试验的两个事件且P(A)＞0，则称:

为在事件A已经发生的条件下，事件B的发生的条件概率。

归纳出条件概率具有的性质:

(1)非负性:0≤P(B|A)≤1;

对于初学者，在讲解条件概率时，需要强调P(B)，P(B|A)和P(BA)所表示的意义是不同的，P(B|A)表示条件概率，P(BA)表示事件A和事件B同时发生的概率。由式(1)可以推导出乘积公式如下:

乘积公式［3］:

设 P(A)＞0，则有 P(AB)=P(A)P(B|A);若 P(B)＞0，则有P(AB)=P(B)P(A|B)。

将两个事件的乘积公式推广到有限个事件的乘积公式:若P(A1A2……An－1)，则有P(A1A2……An)=P(A1)P(A2|A1)P(A3|A1A2)…P(An|A1A2……An－1)。

为了巩固学生对条件概率和乘积公式的认识，让学生独立完成下题。

习题1 一批产品有10件，其中6件正品，4件次品，从中任取两次，每次任取一件，采取非回置抽样，求:①两次都取到正品的概率;②第一次取到次品，第二次取到正品的概率。

解 设A表示“第一次取到是正品”，B表示“第二次取到是正品”。

对于①:两次都取到正品的事件是AB，则P(AB)=P(A)P(B|A)

2 条件概率的实际应用

由条件概率推导出的全概率公式和贝叶斯公式是用来解决实际生活中的问题，应用价值很高，学生对公式掌握的程度，直接决定了学生解决问题的能力。通过多年对《概率论与数理统计》课程的教学研究，发现从实例入手，引导启发学生学习全概率公式和贝叶斯公式的效果甚好。

2.1 全概率公式的教学方法

基于学生高中时掌握的概率知识，引导学生解决下列问题:

引例2 在一盒中装有10只乒乓球，其中8只新球，第一次比赛时从中任取两球，赛后仍放回原盒子，第二次比赛时，再从盒子里取两个球，求第二次取出的两个球都是新球的概率。

解 让学生利用高中的已有的概率知识分析问题，学生很快发现第二次试验取得两球的新旧，受到第一次试验取得两球新旧的影响，故先对第一次取得两个球进行分类:

① 事件A0:新球0个，旧球2个;② 事件A1:新球1个，旧球1个;③ 事件A2:新球2个，旧球0个。

设第一次试验的样本空间为Ω，则A0，A1，A2两两互不相容且A0∪A1∪A2=Ω，即A0，A1，A2是Ω一个完备事件组，设B表示第二次取出的两个球都是新球，由题意可知P(B|A)=0

利用互不相容事件的可加性和条件概率及乘积公式可得:

对解题过程进行总结，B事件发生之前受到前一次试验结果的影响，且A0，A1，A2是前一次试验的一个完备事件组，则B事件发生概率为P(B)=)，将解题方法一般化就得得到了全概率公式。

全概率公式［3］设试验E的样本空间为Ω，A，A…A为一完备事件组，且P(A)＞ 0，i=1，2，…，n，则12ni对任一事件B，有P(B)=

全概率公式适用范围:对于事件B，它的发生受到前一次试验结果的影响，且A1，A2…，An是前一次试验的一个完备事件组，则在计算P(B)时，将复杂的事件B分成分类进行考虑，再利用全概率公式解出P(B)。

下面贴近生活的实际问题既可以巩固全概率公式，又可以引入贝叶斯公式。

引例3 一人到达目的地乘火车、船、汽车和飞机的概率分别为0.3、0.2、0.1和0.4，并且迟到的概率分别为0.25，0.3，0.1和0，求① 此人迟到的概率;② 如果此人迟到，他乘坐哪种交通工具的可能性最大。

解 令A1，A2，A3，A4表示此人选择的交通工具分别为火车、船、汽车和飞机，B表示此人迟到。对于①:B事件发生与此人选择的交通工具有关，且A1，A2，A3，A4是一完备事件组，全概率公式的适用范围可知，计算P(B)需要使用全概率公式，即P(B)=)，由题意可知 P(A1)=0.3，P(A2)=0.2，P(A3)=0.1，P(A4)=0.4，P(B|A1)=0.25，P(B|A2)=0.3，P(B|A3)=0.1，P(B|A4)=0，从而P(B)=0.145。

对于②:已知B事件发生，显然利用条件概率求出结果。

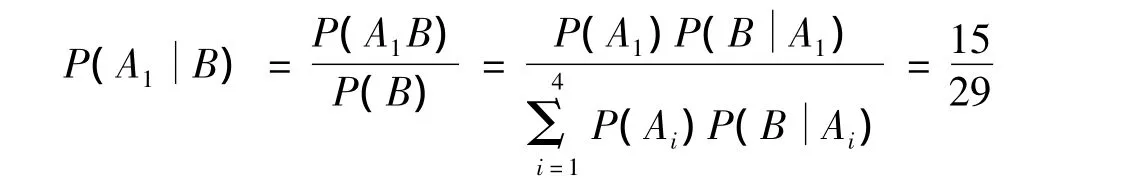
对问题③的做题过程进行归纳得出贝叶斯公式如下:

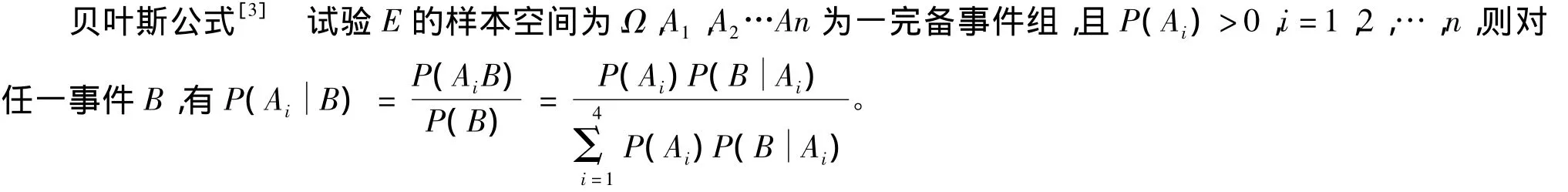
贝叶斯公式适用范围:已知B事件已经发生，且引起B事件发生的可能“原因”共有n个，分别为A1，A2，…，An且两两互不相容，此时可以利用贝叶斯公式计算出每个)，然后找出其中最大的一个P)，则Ai就是引起B事件发生的最大可能的原因。

［1］华东师范大学数学系.概率论与数理统计［M］.北京:高等教育出版社，1994

［2］丁万鼎.概率论与数理统计［M］.上海:上海科学技术出版社，1999

［3］杨桂元.概率论与数理统计［M］.成都:电子科技大学出版社，2002

［4］李明泉.全概率公式和贝叶斯公式教学琐谈［J］.武汉工程职业技术学院学报，2007，19(4):76-78

［5］宋明珠.随机环境马氏链的常返性与暂留性［J］.重庆工商大学学报，2009，26(3):209-112