带多重临界指数和Hardy项的椭圆方程组解的存在性

康东升,张微微,吴 红

(中南民族大学 数学与统计学学院,武汉 430074)

1 问题的引入

本文研究下列椭圆方程:

(1)

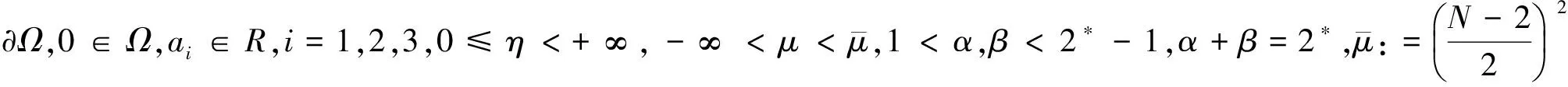
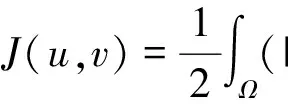
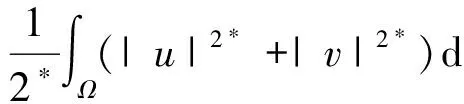
则J∈C1(H×H,R).我们称(u0,v0)∈H×H是方程组(1)的解，如果：

u0,v0≠0,〈J′(u0,v0),(φ,ø)〉=0,

∀(φ,ø)∈H×H.

研究方程组(1)涉及到Hardy不等式[1]:

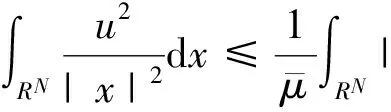
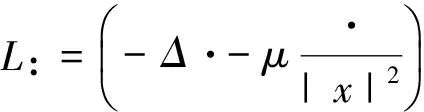
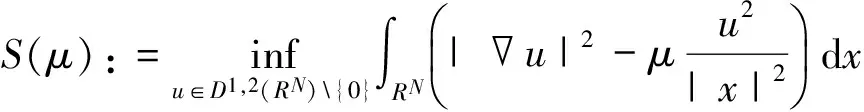
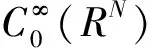
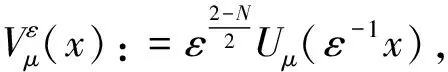
(2)

Uμ(x)是径向对称函数，Uμ(x)=

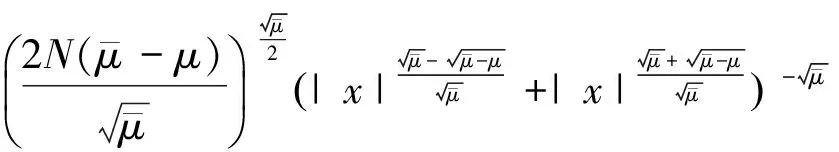
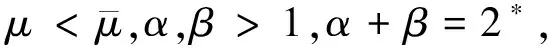
Sη,α,β(μ):=

近年来带有Hardy项和临界Sobolev指数的方程受到关注,参见文[1]，[2]，[3]，[5]-[8]及其参考文献,但上述文献主要是研究单个椭圆方程,关于椭圆方程组的结果很少.本文主要研究方程组(1)当ai(1≤i≤3)取值范围较大时,非平凡解的存在性.

在本文中我们做以下假设：

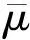
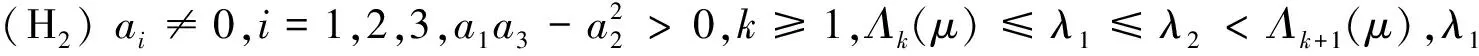
(H3)a2≠0,并且存在常数θ1,θ2∈R+,k,k′∈N+,满足：

Λk(μ)≤a1-θ1|a2|,a1+θ2|a2|<Λk+1(μ),

Λk′(μ)≤a3-(θ1)-1|a2|,a3+(θ2)-1|a2|<

Λk′+1(μ).

定义二次型

Q(u,v):=(u,v)A(u,v)T=a1u2+2a2uv+a3v2.

如果(H2)成立，则有：

λ1(u2+v2)≤Q(u,v)≤λ2(u2+v2),∀(u,v)∈H×H.

(3)

在条件(H3)下有：

(4)

注意(3)式和(4)式系数区域不同,在(H2)和(H3)中条件a2≠0用来排除方程组(1)的半平凡解.

记d*:=max{|x|2,x∈∂Ω},

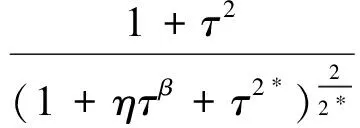
其中τmin≥0是f(τ)的最小值点.

本文的主要结果如下.

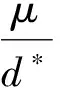
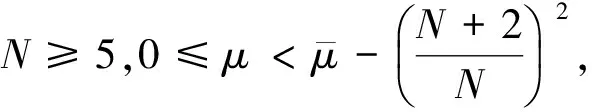
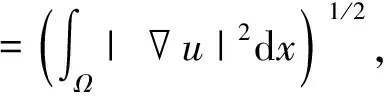
2 解的存在性

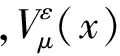
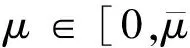
(ii)Sη,α,β(μ)=f(τmin)S(μ)=f(τmin)S(0)=Sη,α,β(0),∀μ∈(-∞,0].

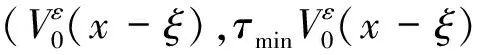
设ei(x)为对应于λi(μ)的特征函数，i∈N,k∈N,H(k)表示由对应于特征值λ1(μ),λ2(μ),…，λk(μ)的L2范数单位化的特征函数张成的空间，取m∈N足够大使得B2/m(0)⊂Ω. 定义：

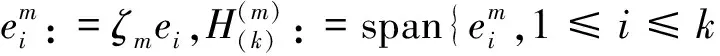
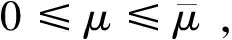
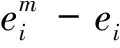
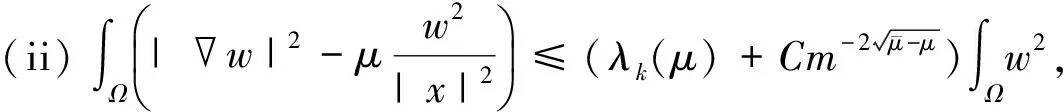
设μ<0且ξ∈Ω,取m∈N足够大使得B2/m(ξ)⊂Ω{0}. 定义：

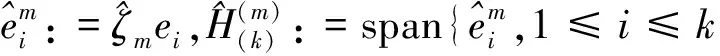
引理4 设-∞<μ<0,则：

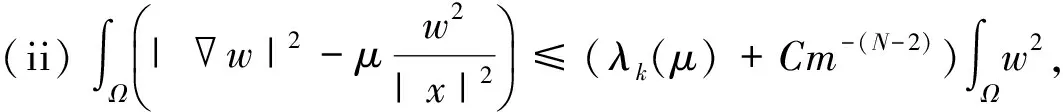
证明(i)参见文献[3]中引理1的证明.

(ii)当μ≤0时，ei∈L∞(Ω).证明方法与文献[7]中引理2.3相同.

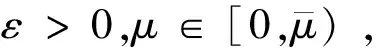
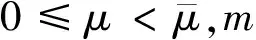
(5)

(6)

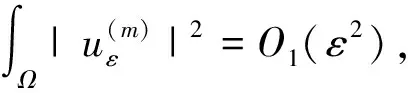
(7)

同样地，当ξ∈Ω,m∈N充分大，定义：

由引理5的证明过程，可以得到下面的引理6.证明略去.

引理6[8]设m充分大，ε=o(m-1)，则：

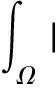
对于ρ>0，定义下面的符号:

Bρ={(u,v)∈H×H|‖(u,v)‖<ρ},

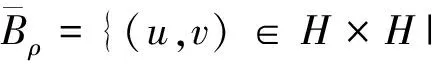
∂Bρ={(u,v)∈H×H|‖(u,v)‖=ρ}.

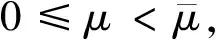
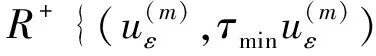
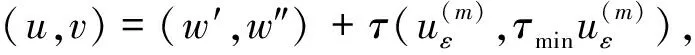
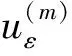
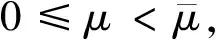
(i)存在σ>0,δ>0,ρ>0,使得：

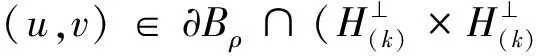
(ii)存在R>ρ,使得：

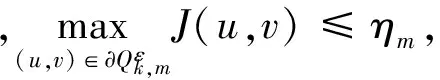
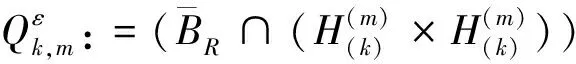
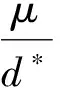
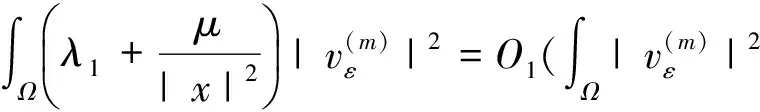
(8)

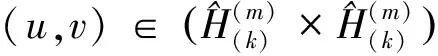
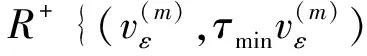
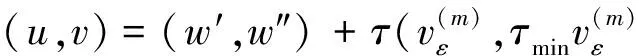
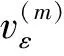
引理8 假设(H1),(H2)成立，且μ<0，则

(i)存在常数σ>0,δ>0,ρ>0,满足：

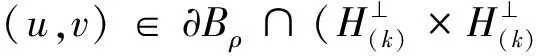
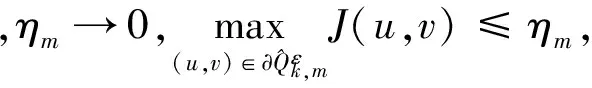
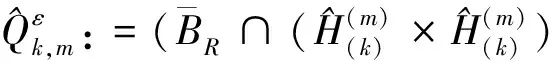
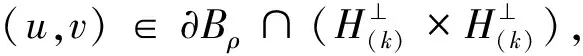
J(u,v)≥

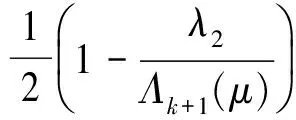
所以当ρ和σ充分小时，结论成立.

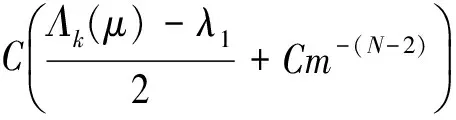
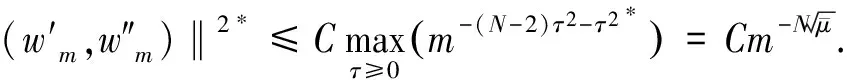
(9)

所以有:

对任意r≥0，

由引理6和(8)式，存在R1满足:

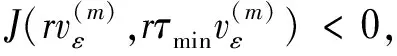
因此，

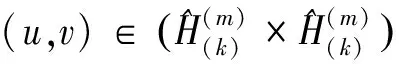
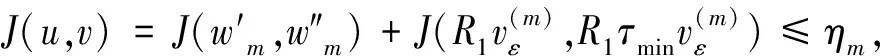
定义

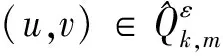
由环绕定理[9]，我们得到J的一个(PS)c序列，由引理1，当ε充分小时就有：

(10)

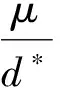
在ε足够小成立. 相反地，假设：

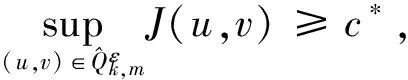
(11)

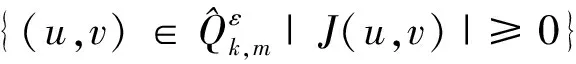
(12)

这里

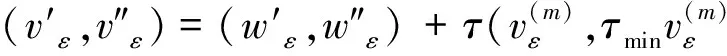
(13)

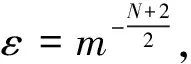
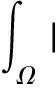
(14)

(15)

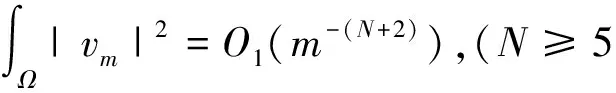
(16)

另一方面，

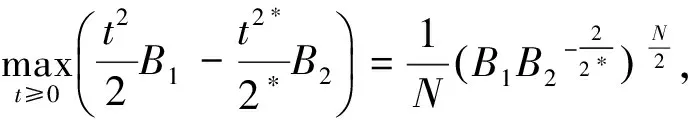
(17)

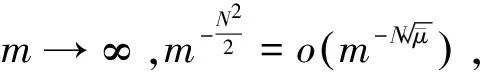
J(τmvm,τmτminvm)≤

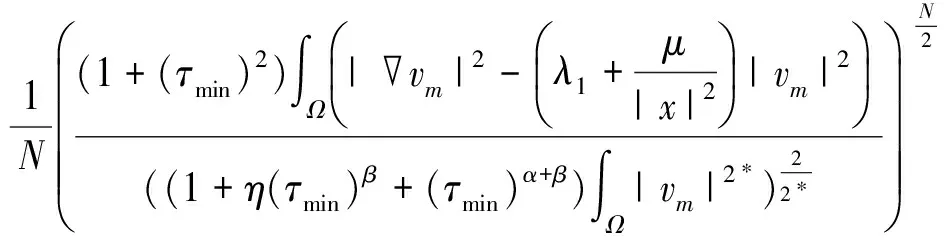
(18)

从(10)和(18)式，得：

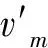
和(12)式矛盾.因此当ε足够小时，

由环绕定理[9]和引理1，方程组(1)有解(u,v)∈H×H. 定理1证毕.

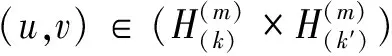
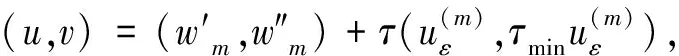
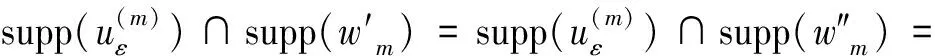
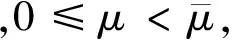
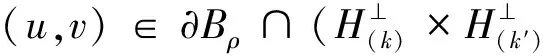
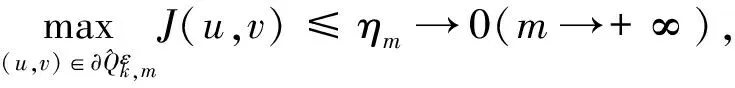
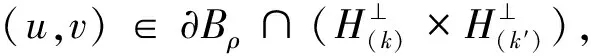
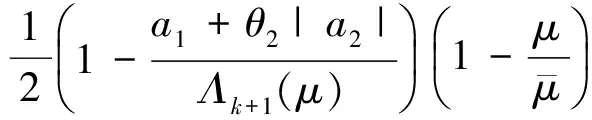
C‖(u,v)‖2*≥C‖(u,v)‖2-C‖(u,v)‖2*.

所以当ρ和σ充分小时，结论成立.

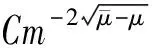
(19)

剩下的证明与文[8]中引理5相似,这里略去.

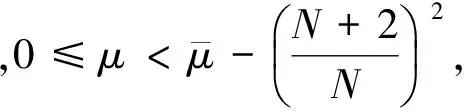
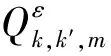
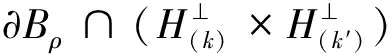
由引理9和环绕定理[9]，我们得到J的一个(PS)c序列，由引理1，我们只需要验证当ε足够小时下式成立：

(20)

由(H3)和(4)式可以得到：

a1u2+2a2uv+a3v2≥(u2+v2)min{a1-θ1|a2|,a3-(θ1)-1|a2|}.

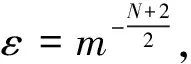
(21)

由 (18)和(21)式可知当m足够大时(20)式成立，从而结论成立.

[1] Hardy G,Littlewood J,Polya G.Inequalities[M].Cambridge: Cambridge University Press,1988: 239-243.

[2] Egnell H.Elliptic boundary value problems with singular coefficients and critical nonlinearities [J].Indiana Univ Math,1989,38(2): 235-251.

[3] Talenti G.Best constant in Sobolev inequality[J].Ann Mat Pura Appl,1976,110(1): 353-372.

[4] Terracini S.On positive solutions to a class of equations with a singular coefficient and critical exponent [J].Adv Differential Equations ,1996,2(2): 241-264.

[5] Huang Y,Kang D.On the singular elliptic systems involving multiple critical Sobolev exponents [J].Nonlinear Anal,2011,74(1): 400-412.

[6] Cao D,Han P.Solutions for semilinear elliptic equations with critical exponents and Hardy potential [J].J Differential Equations,2004,205(1): 521-537.

[7] Ferrero A,Gazzola F.Existence of solutions for singular critical growth semilinear elliptic equations [J].J Differential Equations,2001,177(1): 494-522.

[8]康东升，吴 红，张微微.带有多重临界指数的椭圆方程组的非平凡解[J].中南民族大学学报：自然科学版,2013(1): 92-96.

[9] Rabinowitz P.Minimax methods in critical points theory with applications to differential Equations [M].Washington: American Mathematical Society,1986: 7-50.