Approximate Failures Semantics for Polynomial Labelled Transition Systems
WANG Chao( ),LIANG Yi( ),WU Jin-zhao(),TAN Hong-yan()
1 School of Computer and Information Technology,Beijing Jiaotong University,Beijing 100044,China
2 Guangxi Key Laboratory of Hybrid Computation and IC Design Analysis,Guangxi University for Nationalities,Nanning 530006,China
3 Institute of Actuaries,Chinese Academy of Sciences,Beijing 100190,China
Introduction
The labelled transition system (LTS)[1]consists of a set of states and transitions between states.The transitions are labeled from a given set.Traditionally,the labels of LTS are abstract.They can represent different things depending on the problem of interest.Typically,the usages of labels include representing expected inputs (such as used in finite state machine),actions that performed during the transitions (such as used in process algebra),conditions that must be true to trigger the transitions (such as used in event condition action),and mixtures,for example,mixing conditions and time intervals (such as used in timed event level structure).
A new variation of LTS named polynomial labelled transition system (PLTS) is proposed which refines the labels of LTS into multivariate polynomials,under the assumption that the number of variables is finite.A state of PLTS is an interpretation of all variables.Furthermore,the effect of a transition is to update the state by resetting the variables to zeros of the labelling multivariate polynomial.In other words,each transition is decorated with a non-deterministic update from an algebraic set.
The multivariate polynomials have several advantages.Firstly,polynomials enhance the accuracy of description.That is to say,polynomials have a greater ability to characterize behaviors than abstract symbol.For example,an accelerated motionv=2t+1 contains more internal details than an abstract symbola.Secondly,polynomials are the simplest ones among all expressions.For example,polynomials are simpler than transcendental expressions (e.g.,exponential expressions and logarithmic expressions).Thirdly,polynomials have a very broad application since there are many well-developed theories of them.For example,computers can directly evaluate polynomials,and many expressions (e.g.,trigonometric expressions) can be approximated by polynomials.More important,Weierstrass Approximation Theorem tells us that the error of using polynomial approximation is under control when a continuous function is defined on the real interval.To sum up,refining abstract labels into multivariate polynomials has both theoretical and practical relevance.
Based on the theory of numerical approximations,the following reduction methods will be used on labels of PLTS.
(1) Replace polynomial labels under zeros equivalence.(e.g.,x2=0 andx=0 are equivalent.)
(2) Simplify polynomial labels by using Taylor expansion,the best first order approximation or other approximation methods.
(3) Decompose complex polynomial labels into several simple polynomial labels by using cubic spline interpolation,piecewise linear interpolation or other approximation methods.
The methods above simplify polynomials and hence reduce the computational complexity.Besides,they create opportunities for using linear time-branching time spectrum behavioral equivalences[2-3]which minimize PLTS by decreasing the number of states.
Various semantics equivalences are applied in finitely branching,concrete,sequential,nondeterministic processes[2-3],where finitely branching means there are only finitely many possible ways that a process can proceed in each state,concrete means a process does not have internal actions,sequential means it can perform at most one action at a time,and nondeterministic means a process after a trace may arrive at different states.It is noted that these processes may have infinite length actions.
In this paper the failures semantics is focused on which is introduced by Brookesetal.[4]The motivation for failures semantics is presented in Ref.[5].The intersection operator[6]is also called synchronous parallel composition,which allows an action to happen only if it can happen on both sides of the operator.A process reaches a state of deadlock[7]when it can carry out no further actions.Failures semantics supports both intersection operator and deadlock behaviour,and it is the coarsest semantics supporting both of them among all semantics reviewed in linear time-branching time spectrum[2].
In recent years,many researchers have taken failures semantics as one of the standard denotational semantics[8-9]of communicating sequential processes (CSP).However,existing researches ignore the concept of approximation which has a great potential to improve the computation efficiency.
A similar definition to PLTS is algebraic transition system[10-11].However,algebraic transition system must employ current-state variables and next-state variables,and have initial conditions,while the PLTS does not have these restrictions.
1 Polynomial Labelled Transition System (PLTS)
This section presents the definition of polynomial labelled transition system (PLTS) and our replacement theorem.
Definition1A PLTS is a tuple

Fig.1 An example of PLTS
In a PLTS model diagram,states are represented by circles,and transitions from states to states are represented by edges and multivariate polynomials labelled on them.Figure 1 is an example of PLTS model diagram.The stateS1may perform an actionx-1 to reach the next stateS2,then it may do an actiony-xto reach the stateS3or do an actiony-x-1 to reach the stateS4.The choice betweeny-xandy-x-1 is interleaving concurrency.V={x,y},S={S1,S2,S3,S4},and the states are listed in Table 1.

Table 1 The states of Fig.1

The following are the symbols used in the paper.Ø denotes the empty set.εdenotes the empty sequence of polynomials.Zeros(a) denotes the zeros ofa∈Awith variable names.HenceZeros(x-1) is different fromZeros(y-1),whileZeros(x2) andZeros(x) are equivalent.

Theorem1says that a complex polynomial can be replaced by a simple one which has the same zeros to reduce the computational complexity.
Section 2 introduces the numerous advantages of multivariate polynomials.Since polynomial is more satisfactory in describing behaviour than abstract action,the scope of the problems which PLTS can solve is larger than that LTS can do.Although PLTS is more complex than LTS,the former can become simpler with the help of rich theory of numerical approximations.The technique of approximation is introduced in the next section.
2 Approximation
This section introduces a number of numerical approximation theorems,which are illustrated in the case studies and used to reduce the computational complexity.

(1)
xn+a1xn-1+…+an-1x+an=0,
(2)
xn+a1xn-1+…+an-1x+an+ω=0.
(3)


ProofByLemma1,subtract Eq.(3) from Eq.(2),yields:
…+an-2(x2+x1)+an-1}+ω

|ω|
The idea ofTheorem2is a bit like interval polynomials[12].Theorem2can be generalized to a multi-variable version.The conclusions above remain valid when the disturbance term is related to other coefficient (e.g.,a1) .
Theorem3Iff(x) has a continuous second derivative in the interval [a,b],then the piecewise linear interpolationL(x) satisfies
Theorem4Iff(x) has a continuous second derivative in the interval [a,b] and the derivative does not change sign,then the best first order approximationp(x) satisfies
Theorem5Taylor’s theorem: iff(x) isk(an integer,k≥1) times differentiable at the pointa,there existshk(x) such that

Iff(x) isk+1 times differentiable on the open interval and continuous on the closed interval betweenaandx,Lagrange form of the remainder is

whereξis betweenaandx.

Theorem5can also be used in estimating the total error after propagation of errors.The technique is detailed in Section 4.3.Theorem6guarantees that there exists an approximated polynomial,given a error limit.Hence,the error of using polynomial approximation is under control.
3 Failures Semantics
This section describes the definitions of Failures semantics.

Let Power(A) denote the power set ofA.With the help of definition of initial actions,the definition of failure pair is as follows.

A failure pair <δ,X> of a processprecords that the actions setXis refused by the processpafter a certain sequence of actionsδ.The set of all failure pairs of the processpis denotedF(p),called the failures set ofp.The set is used to determine whether a process is failures equivalent with another process.
Definition4Two processespandqare failures equivalent,notationp=Fq,iffF(p)=F(q).
Ifp=Fq,then in failures semanticspandqare identified,that is to say there is no difference betweenpandqunder failures semantics.Besides that,one and only one process can be constructed under failures semantics equivalence for a given failures set.
Obviously,ifδ∈T(p),<δ,Ø>∈F(p).In order to letT(p) andF(p) have the same form,δis identified with a pair <δ,Ø> in this paper.
For example,the failures set of Fig.1 is {<ε,{y-1}>,<ε,{y-2}>,<ε,Ø>,
Theorem7Failures are finer than completed trace,coarser than readiness semantics and failure trace semantics.
Let CT,F,R,and FT respectively denote completed trace semantics,failures semantics,readiness semantics,and failure trace semantics.Then the relations inTheorem7can be denoted as CT Using behaviour equivalence which alleviates the state explosion problem,a simpler equivalent model can be selected to verify both safety and liveness properties. This section presents three cases studies of our technique which combines approximation and failures semantics equivalence on PLTS. Case 1 illustrates how to transform actual problem into PLTS and use numerical approximation methods to simplify PLTS. Case 2 illustrates our approximate failures semantics for PLTS,namely,combines numerical approximation and failures semantics equivalence. Case 3 illustrates how to estimate total error after propagation of errors. Figure 2 considers a diamond ABCD whose center is O,∠ADC=60°,OA=x,its perimeterp=8 and its areaa=3.464.This implies the following conclusion: (4) p=AB+BC+CD+DA=8x. (5) Equation (4) is a quadratic equation ofx.When solving this equation,using quadratic formula method is denoted asm=1,and using completing the square method is denoted asm=2.There is only one way to solve Eq.(5) which is denoted asm=1.In other words,after calculation of Eq.(4) there are two options (m=1,m=2) which can be chosen,and after calculation of Eq.(5) there is only one option (m=1).Then this problem corresponds to PLTS model diagram (Fig.3). Fig.2 A diamond Fig.3 PLTS model Fig.4 Numerical approximation Since the failures set of Fig.4 has a failure pair Fig.5 Another PLTS model Fig.6 Original model(x∈[0,2]) Fig.7 Best first order approximation The failures set of Fig.7 is {<ε,{y-7x+6,y-x}>, <ε,{y-7x+6}>, <ε,{y-x}>, <ε,Ø>, A new PLTS model (Fig.8) can be generally constructed which matches the failures set expression above.Hence,Figs.8 and 7 are equivalent under failures semantics. Fig.8 failures semantics equivalence To sum up,under the conditionez≤0.107,Fig.6 is approximately failures semantics equivalent to Fig.8.Intuitively,Fig.8 has lower computational complexity and a smaller number of states than Fig.6.So it is more efficient to use PLTS model (Fig.8) instead of PLTS model (Fig.6) in formal description and verification. In a multi-step PLTS model,the errors arising due to numerical approximation will propagate.The following case (Fig.9) describes a generic approach which is used to estimate total error after propagation of errors. F ig.9 Original model x∈[0,] In other words,z-y3is decomposed intoz-4.75y+3.75 andz-9.25y+10.5.Decomposition methods,which are somewhat analogous to action refinement methods,reduce the computational complexity but increase the number of states.So it requires further discussion about the advantages and disadvantages of each decomposition.The branch introduced by a piecewise function can be regarded as system choice.Hence Fig.9 is approximate to Fig.10 under the condition thatey≤0.092 andez≤0.375. Fig.10 After approximation The following will be derived fromTheorem5Taylor’s theorem and Lagrange form of the remainder, 9.25ey≤0.849 The error estimate method above can be always applied in the approximation on PLTS,even though the approximation takes place in the beginning of multi-step PLTS model. A new variation of LTS named PLTS is proposed,which is used to extend the power of the model of LTS by specializing abstract labels as multivariate polynomials.The motivation comes from the need to improve the accuracy of description.The main advantage of PLTS is its great potential to alleviate the computational complexity and cut down the scale of PLTS since it is convenient to make full use of approximations of numerical computation and behavioural equivalence.The approximation methods include replacing polynomial labels,simplifying polynomial labels,and decomposing complex polynomial labels into several simple polynomial labels.For behavioural equivalence,in this paper failures semantics equivalence under polynomial form is focused on.All the methods above rebuild the PLTS model and gains in simplification and downsizing.Our methods will save a lot of work in formal description and verification. Decomposition method reduces computational complexity.The drawback of this method is that it increases the number of states.Hence it requires further discussion about the advantages and disadvantages of each decomposition.But it is still worth doing decomposition when it requires a very high running efficiency or it is time sensitive. The condition introduced by decomposing polynomial labels can be viewed as system choice,which can be amended by adding semi-algebraic feature to PLTS.Polynomials in PLTS have many features and only a small part of them has been studied in this paper.It would be one of the most controversial issues in the future and will be studied in our future work. [1] Keller R M.Formal Verification of Parallel Programs[J].CommunicationsoftheACM,1976,19(7): 371-384. [2] van Glabbeek R J.The Linear Time-Branching Time Spectrum I-the Semantics of Concrete,Sequential Processes[M]// Bergstra J A,Ponse A,Smolka S A.Handbook of Process Algebra.New York: Elsevier Science Inc.,2001: 3-99. [3] Maldonado A P,Monteiro L,Roggenbach M.Towards Bialgebraic Semantics for the Linear Time-Branching Time Spectrum[C].Proceedings of the 20th International Conference on Recent Trends in Algebraic Development Technique,Salamanca,Spain,2012: 209-225. [4] Brookes S D,Hoare C A R,Roscoe A W.A Theory of Communicating Sequential Processes[J].JournaloftheACM,1984,31(3): 560-599. [5] Main M G.Trace,Failure and Testing Equivalences for Communicating Processes[J].InternationalJournalofParallelProgramming,1987,16(5): 383-400. [6] Hoare C A R.Communicating Sequential Processes[J].CommunicationsoftheACM,1978,21(8): 666-677. [7] de Boer F S,van Eijk R M,van der Hoek W,etal.Failure Semantics for the Exchange of Information in Multi-Agent Systems[C].The 11th International Conference on Concurrency Theory,University Park,PA,USA,2000: 214-228. [8] Dunne S.Termination without Checkmark in CSP[C].The 17th International Symposium on Formal Methods,Limerick,Ireland,2011: 278-292. [9] Maldonado A P,Monteiro L,Roggenbach M.Towards Bialgebraic Semantics for the Linear Time-Branching Time Spectrum[C].Proceedings of the 20th International Conference on Recent Trends in Algebraic Development Techniques,Salamanca,Spain,2012: 209-225. [10] Sankaranarayanan S,Sipma H B,Manna Z.Non-linear Loop Invariant Generation Using Gröbner Bases[J].ACMSIGPLANNotices,2004,39(1): 318-329. [11] Maza M M,Xiao R.Generating Program Invariants via Interpolation[EB/OL] (2012-01-24)[2012-12-02].http://arxiv.org/abs/1201.5086. [12] Ferreira J A,Patrcio F,Oliveira F.On the Computation of Solutions of Systems of Interval Polynomial Equations[J].JournalofComputationalandAppliedMathematics,2005,173(2): 295-302.4 Case Studies
4.1 Numerical approximation





4.2 Approximate failures semantics




4.3 Propagation of errors







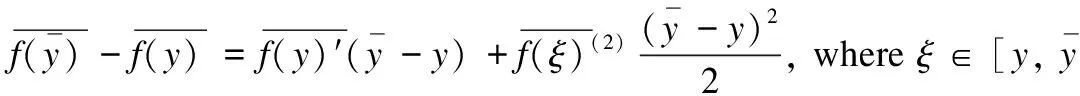


5 Conclusions
 Journal of Donghua University(English Edition)2013年6期
Journal of Donghua University(English Edition)2013年6期
- Journal of Donghua University(English Edition)的其它文章
- Comparison of the Vortex and Ring Spun Cotton Yarns and Their Knitted Fabric Properties
- Modeling of the Dyeing Uptake Rate for Direct Dyestuff on Cotton in Batch Dyeing Process Based on Grey System Theory
- Curing Behaviors and Thermal Properties of Dimer Fatty Acid(DFA) Modified Multifunctional Epoxy Resin
- Scheduling Multiple Orders per Job with Multiple Constraints on Identical Parallel Machines
- Determination Method on Initial Pretension of Cables in Steel Mega Frame and Pre-stressed Composite Bracing Structure
- Mechanical and Abrasion Properties of Polyethylene Terephthalate Films Coated with SiO2/Epoxy Hybrid Material
