基于双层位势的Poisson方程无奇异方法

林 鑫，高发玲

（青岛理工大学 琴岛学院，山东 青岛 266106）

0 引言

在用传统边界元法求解位势问题时，通常需要求解奇异积分，特别是当公式中有双层位势的法向导数时，会遇到超强奇异积分计算。孙焕纯等［1］采用的虚边界法是基于虚拟边界上的单层位势表达式来推导虚边界积分方程，可避免传统边界元中强奇异积分的计算。受此启发，本文利用在虚边界上分布的虚拟密度函数，得出一种基于双层位势的虚边界积分方程，这种间接边界积分公式的优点在于，积分点和场点分别位于虚边界和实边界上，可避免强奇异积分和超强奇异积分的计算。针对求解Poisson方程的3类边值问题，应用这种思想建立了虚边界元求解公式并用配置法求解，最后通过算例来验证方法的有效性和精确性。

1 基于双层位势的虚边界积分方程

不妨考虑二维位势问题。设在以Γ为边界的区域Ω上定义位势函数u，满足Poisson方程位势u可以用单层位势或双层位势分别表示，也可以用两者的组合表示［2］。如果将u的法向导数以连续穿越Γ的方式延拓到Ω的补域，则位势u适合用双层位势表示。不妨在Ω的补域中设置一条与原边界Γ成相似比的虚拟闭曲线，称之为虚边界，记为 Γ′，则在以 Γ′所围的区域Ω′内（见图1），得到u的双层位势表达式

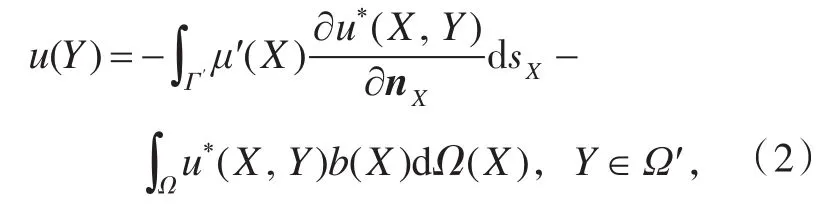
同时，其法向导数为

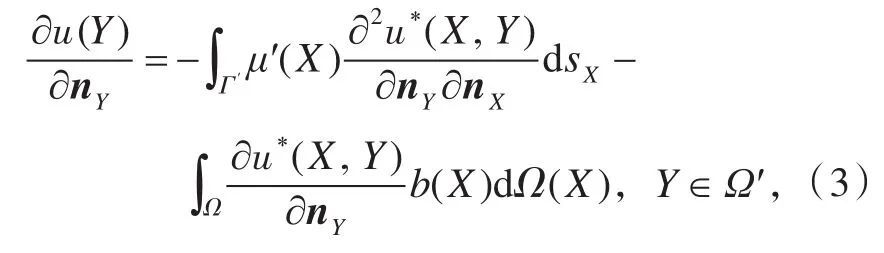
其中μ′是分布在虚边界 Γ′上的虚拟密度函数，简称矩密度；u*（x,y)=-ln|x-y|是二维 Laplace方程的基本解，是对虚边界 Γ′的外法线方向n的导数。

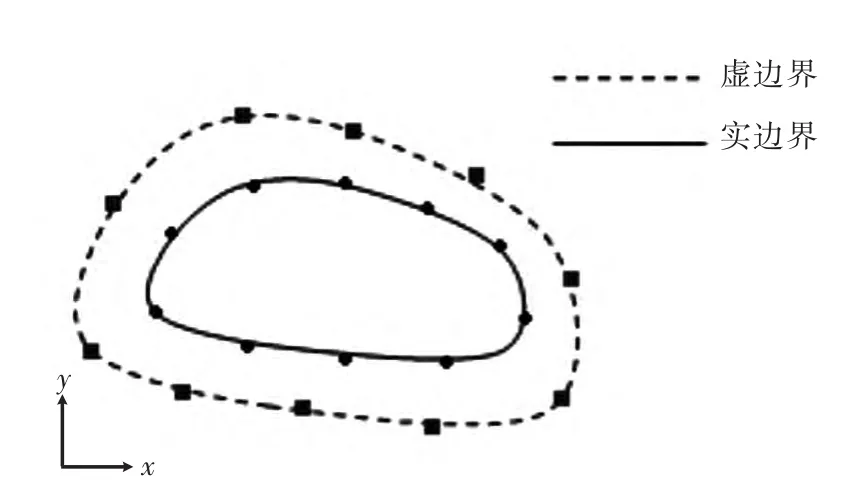
图1 虚实边界及配点示意图Fig.1 Physical，virtual boundary and point collocation

当Y位于原边界Γ时，积分式（2）和（3）仍然成立。此时方向nY为Y点处对Γ的单位外法向量。由于点X和Y分别位于虚实边界，故积分式（2）和（3）不再有奇异性。不妨以Poisson混合边值问题为例得出如下的基于双层位势的无奇异虚边界积分方程组

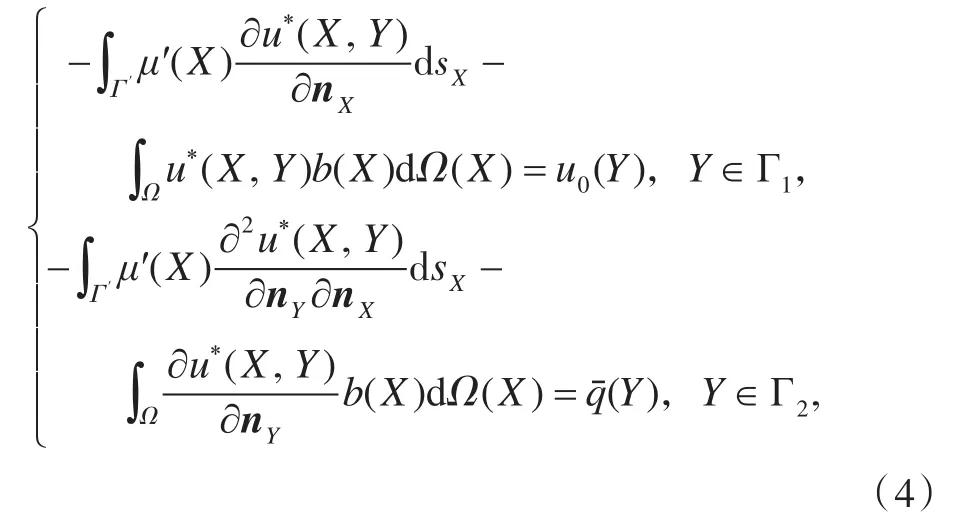
边界积分方程组（4）是间接积分方程，其解具有存在唯一性［3］。通过常单元离散以及m-Gauss积分公式，可以将方程组（4）离散成形如Hμ′=F 的线性代数方程组。解出μ′(X)的值后，再回代到（2）和（3）式的右端，即可求得区域Ω或其边界Γ上任意一点处未知的位势值及其法向导数值。当然，此方法的求解精度在很大程度上受虚实边界之间距离的影响。为此，引入参数λ为虚实边界长度的相似比值［4］，即

通过计算知，对内问题的比值在1.3～7.0间选取，对外问题一般在 0.6～0.8［1，4］内变动。

2 算例

考虑如图2所示的正方形区域的Poisson混合边值问题［5］，其解析解为 u=y(y+1)。 在计算中，首先考虑虚实边界比例对于计算结果的影响，部分内点位势值见表1。

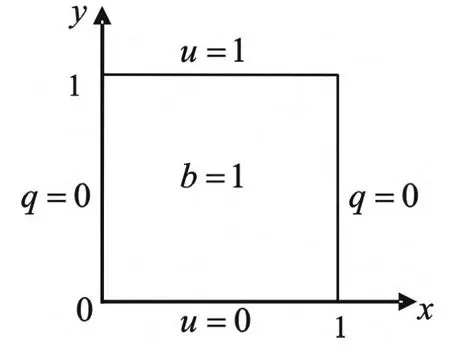
图2 算例的边界条件Fig.2 Boundary condition of example

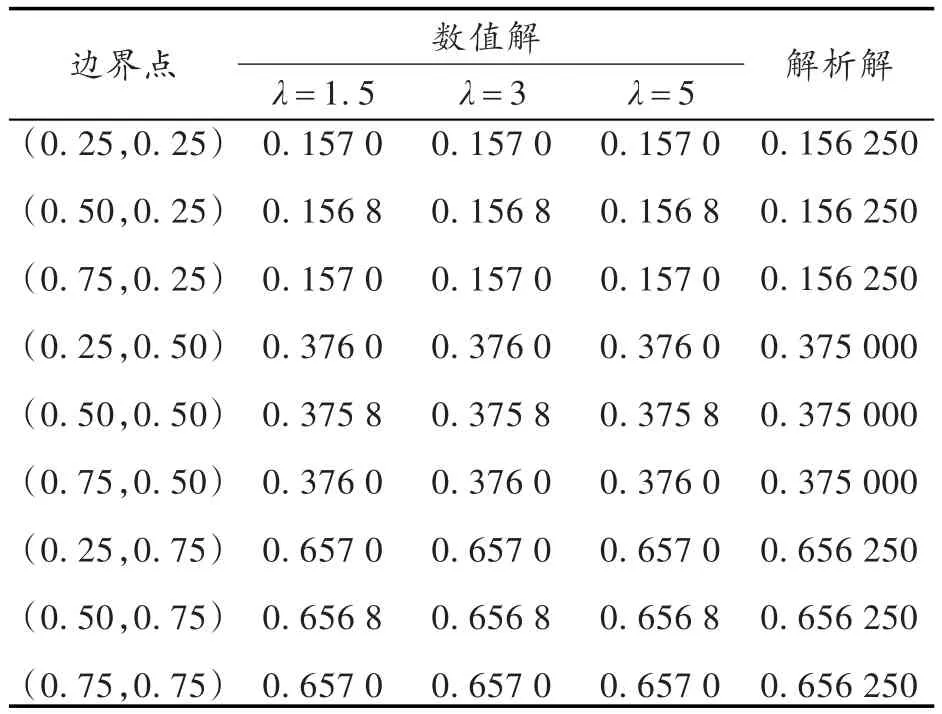
表1 区域内点位势值uTab.1 Potentialuat internal points

由表1可以看出，虚实边界之间的比值可以在1.3～7.0的合理范围内变动而对计算结果的精度并无很大的影响，但是虚实边界之间的距离不可以太近。接着，根据不同边界剖分数目所得到的结果绘出误差图（见图3），从图3可以看出计算结果的精度会随着区域剖分的加密而提高。

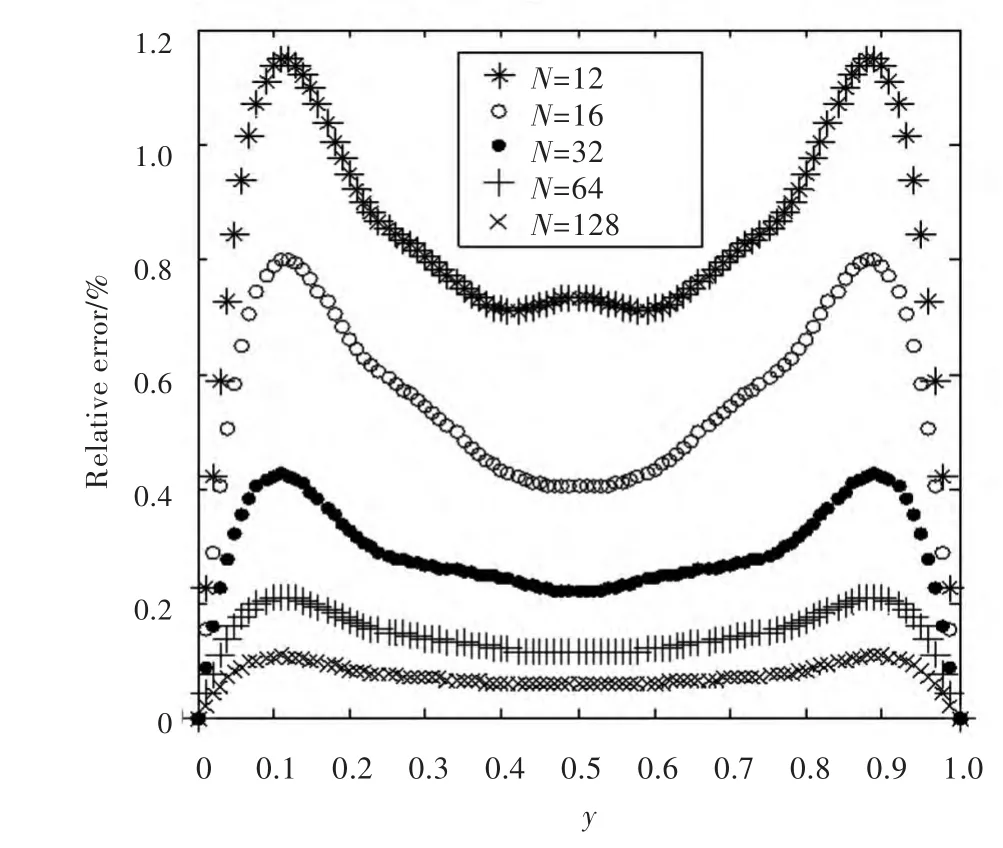
图3 不同边界剖分对应的结果误差图Fig.3 Relative error of different boundary elements

3 结论

对于求解Poisson方程，本文采用了一种完全无奇异性的边界元方法。通过数值试验可以看出：计算结果的精度与虚实边界之间的相似比以及节点数目有一定的关系。对于虚实边界距离，在1.3～7.0范围内都会取得比较好的数值计算结果，但是两者之间不可以太近（即 λ接近于1）。与普通边界元法相比，本方法只需用较少的边界节点数就可以得到相对较高的精度，而且完全避免了奇异与强奇异积分的计算。

（References）

［1］孙焕纯，张立洲，许强，等，无奇异边界元法［M］.大连：大连理工大学出版社，1999：1-25.

［2］祝家麟，袁政强.边界元分析［M］.北京：科学出版社，2009：33-37.

［3］STROUD A H，SECREST D.Gaussian quadrature formulas［M］.Upper Saddle，NJ：Prentice-Hall，1966：78-90.

［4］WANG H，QIN Q H.A meshless method for generalized linear or nonlinear Poisson-type problem［J］.Engineering Analysis with Boundary Elements,2006（30）：515-521.

［5］王元淳.边界元法基础［M］.上海：上海交通大学出版社，1988：83-85.