锥壳中严格集压缩映射的若干新不动点定理

陈树佳，许绍元

(韩山师范学院 数学与统计学系，广东 潮州 521041)

锥壳中严格集压缩映射是一类十分重要的非线性算子，广泛存在于非线性微分方程之中，其中严格集压缩映射不动点定理在研究非线性微分方程解的存在性方面具有十分重要的作用[1-3].近年来，人们在锥壳中严格集压缩映射的研究方面已取得了一些成果，如：文献[4]利用锥壳中严格集压缩映射的一个基本不动点定理，在适当的边界条件下得到了锥壳中严格集压缩映射的新不动点定理；文献[5-10]得到了锥壳中严格集压缩映射的Altman定理、Roth定理和Petryshyn定理及其各种推广形式.本文利用锥壳中严格集压缩映射的Leray-Schauder不动点定理，在适当的边界条件下，得到了锥壳中严格集压缩映射的新不动点定理，进一步改进了文献[4]中的一些结果.

设E是实Banach空间，D⊂E,A∶D→E是连续算子.称A∶D→E是k-集压缩映射，如果存在常数k≥0，使得对任何有界集S⊂D，都有α(A(S))≤kα(S),其中α(S)表示Kuratowski非紧性测度,α(S)=inf {δ>0|S是有限个直径小于等于δ的集合之并}.

定义1[1]映射A∶D→E称为严格集压缩映射，如果存在常数0≤k<1，使得A∶D→E为k-集压缩映射.

1 主要结果

首先给出凸壳中严格集压缩映射的一个基本不动点定理.设E是Banach空间，C⊂E为E的一个闭凸子集且满足条件：对任意α≥0,β≥0以及u,v∈C有αu+βv∈C.设ρ>0，记

Bρ={x:x∈C,‖x‖<ρ},

Sρ={x:x∈C,‖x‖=ρ}.

x≠λAx,∀x∈SR,∀0<λ<1

(1)

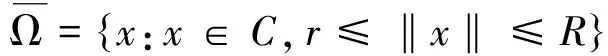
由引理1可以得到凸壳中严格集压缩映射的若干新不动点定理.

‖Ax-x‖α‖x‖β≥‖Ax‖α‖Ax+x‖β-‖Ax‖α‖x‖β,∀x∈SR,

(2)

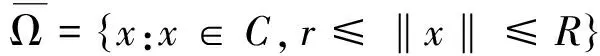
证明若算子A在SR上没有不动点，下证A满足引理1中条件(1)．用反证法．若不然，则存在x0∈SR以及μ0≥1使得Ax0=μ0x0.容易看出μ0>1.考察函数

f(t)=(t-1)α-tα(t+1)β+tα,∀t≥1,

由于f′(t)=α(t-1)α-1-αtα-1(t+1)β+αtα-1-βtα(t+1)β-1≤(<)0,f(t)在[1,∞)上严格单调递减，又当t>1时有f(t)1成立.注意‖x0‖≠0,μ0>1,于是有

‖Ax0-x0‖α‖x0‖β=‖μ0x0-x0‖α‖x0‖β=(μ0-1)α‖x0‖α+β<

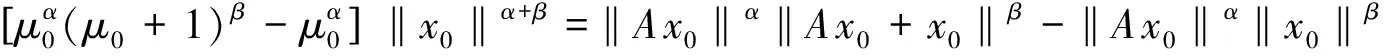
这与(2)式矛盾，故由引理1可知定理1结论成立，证毕.

在定理1的条件中,若分别取α=1,β=1以及α=1，即可以得到以下的两个推论.

‖Ax-x‖‖x‖≥‖Ax‖‖Ax+x‖-‖Ax‖‖x‖,∀x∈SR,

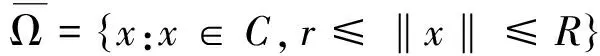
‖Ax-x‖‖x‖β≥‖Ax‖‖Ax+x‖β-‖Ax‖‖x‖β,∀x∈SR,

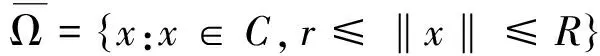
注1显然,文献[4]中推论11(viii)式‖Ax-x‖‖x‖≥‖Ax‖‖Ax+x‖,∀x∈SR蕴含本文推论1的条件：‖Ax-x‖‖x‖≥‖Ax‖‖Ax+x‖-‖Ax‖‖x‖,∀x∈SR.这说明本文推论1推广了文献[4]中的相关结果，而推论2是推论1的进一步推广，故推论2是文献[4]的相关结果的有益补充.

‖Ax+x‖α+β≤‖Ax‖β‖Ax-x‖α+‖x‖α+β,∀x∈SR,

(3)

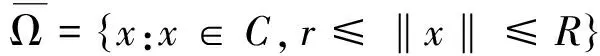
证明若算子A在SR上没有不动点，下证A满足引理1中条件(1)．用反证法．若不然，则存在x0∈SR以及μ0≥1,使得Ax0=μ0x0.容易看出μ0>1.考察函数

f(t)=(t+1)α+β-tβ(t-1)α-1,∀t≥1.

由于f′(t)=α[(t+1)α+β-1-tβ(t-1)α-1]+β[(t+1)α+β-1-tβ-1(t-1)α]>0,f(t)在[1,∞)上严格单调递增，又当t>1时有f(t)>f(1)，即(t+1)α+β>tβ(t-1)α+1对任意t>1成立.注意到‖x0‖≠0,μ0>1，于是有

‖μ0x0‖β‖μ0x0-x0‖α+‖x0‖α+β=‖Ax0‖β‖Ax0-x0‖α+‖x0‖α+β,

此与(3)式矛盾，故由引理1可知定理1结论成立，证毕.

‖Ax+x‖2≤‖Ax-x‖2+‖x‖2,∀x∈SR,

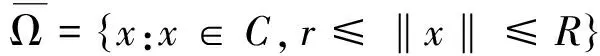
‖Ax+x‖α≤‖Ax-x‖α+‖x‖α,∀x∈SR,

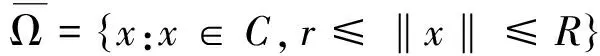
注2推论3类似于著名的Altman定理.因此，推论3是Altman定理的有益补充.由于推论4是推论3的进一步推广，因而推论4是Altman定理的进一步补充.

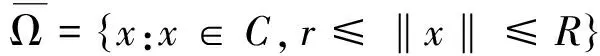
‖Ax‖α‖Ax+x‖β≤‖Ax‖β‖Ax-x‖α,∀x∈SR,

(4)

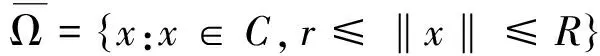
证明若算子A在SR上没有不动点，下证A满足引理1中条件(1)．用反证法．若不然，则存在x0∈SR以及μ0≥1使得Ax0=μ0x0．容易看出μ0>1．考察函数

f(t)=tα(t+1)β-tβ(t-1)α.

由于f′(t)=α[tα-1(t+1)β-(t-1)α-1tβ]+β[tα(t+1)β-1-tβ-1(t-1)α]>0,f(t)在[1,∞)上严格单调递增，又当t>1时有f(t)>f(1)=2β>0，即tα(t+1)β>tβ(t-1)α对任意t>1成立.注意到‖x0‖≠0,μ0>1，于是有

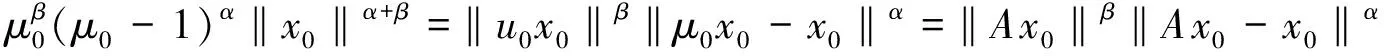
此与(4)式矛盾，故由引理1可知定理3成立，证毕.

在定理3的条件中若分别取α=1,β=0，则有如下推论.

‖Ax‖≤‖Ax-x‖,∀x∈SR,

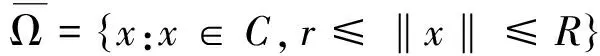
注3推论6即著名的Petryshyn定理[4],因此本文定理3是对Petryshyn定理的进一步推广．

‖Ax-x‖α‖x‖α+β≥‖Ax‖α‖Ax+x‖α+β-‖x‖2α+β,∀x∈SR,

(5)

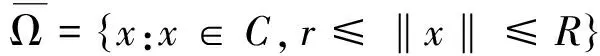
证明若算子A在SR上没有不动点，下面证明A满足引理1中条件(1)．用反证法．若不然，则存在x0∈SR以及μ0≥1,使得Ax0=μ0x0.容易看出μ0>1.考察函数

f(t)=(t-1)α-tα(t+1)α+β+1.

由于f′(t)=α[(t-1)α-1-tα-1(t+1)α+β-tα(t+1)α+β-1]-β[tα(t+1)α+β-1]<0,f(t)在[1,∞)上严格单调递减,又当t>1时有f(t)1成立.注意到‖x0‖≠0,μ0>1，于是有

‖Ax0-x0‖α‖x0‖α+β=‖x0‖α+β‖μ0x0-x0‖α=(μ0-1)α‖x0‖2α+β<

‖Ax0‖α‖Ax0+x0‖α+β-‖x0‖2α+β,

这与(5)式矛盾，故由引理1可知定理4成立，证毕.

在定理4的条件中,若取β=0,则可得到如下推论.

‖Ax-x‖α‖x‖α≥‖Ax‖α‖Ax+x‖α-‖x‖2α,∀x∈SR,

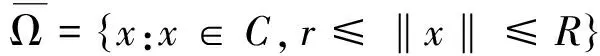
参考文献：

[1]Agarwal R P,Meehan M,O ’ Regan D. Fixed Point Theory and Application[M]. Cambridge: Cambridge University Press and Beijing World Publishing Corporation,2001.

[2]Agarwal R P,O’ Regan D. A note on the existence of multiple fixed point for multivalued maps with applications[J]． J Diff Eqns，2000，160:389-403.

[3]Simon A,Volkmann P. Existence of ground states with exponential decay for semi-linear elliptic equations inRn[J]. J Diff Eqns，1988，76:374-390.

[4]许绍元，谢显华.锥壳中严格集压缩映射的新不动点定理[J].信阳师范学院学报：自然科学版，2011,24(4):440-443.

[5]许绍元.Altman定理的推广与改进[J].江西师范大学学报：自然科学版,1995,19(2):149-152.

[6]许绍元.Banach空间中压缩映射的新不动点定理[J].赣南师范学院学报,2007,28(6):1-4.

[7]郭大钧,孙经先.拓扑度的计算及其应用[J].数学研究与评论,1988,8(3):469-480.

[8]陈继乾.P1-紧与半紧1-集压缩映射的Altman定理[J].工程数学学报,1994,11(2):118-122.

[9]许绍元.P1-紧映象的Altman定理的一个推广[J].江西师范大学学报：自然科学版,1996,20(1):89-91.

[10]贾庆菊.Altman定理的一个注记[J].山西大学学报：自然科学版,1994,17(3):266-268.