一类线性正算子Lp空间逼近的强逆不等式
刘国军,马月梅,张选德
(1.宁夏大学数学计算机学院,宁夏银川750021; 2.宁夏大学民族预科教育学院,宁夏银川750002)
P.N.Agrawal等[1]定义了一类线性正算子

约定Pn,k(x)=0,k<0,并且讨论了该算子对无界函数的同时逼近问题.
文献[2-3]分别讨论了算子Mn(f)的线性组合和迭代线性组合的逼近正定理.文献[4-5]讨论了该算子的线性组合在Lp空间逼近的逆定理和饱和定理.李景斌等[6]进一步讨论了算子Mn(f)在Lp空间逼近的弱型逆定理,即Steckin-Marchaud型不等式.2012年,文献[7]给出了该算子的一种变形.
本文在上述研究的基础上,继续讨论算子Mn(f)在Lp[0,∞)(1≤p≤∞)中的强型逆定理,得到了逼近的强逆不等式.强逆不等式给出了算子逼近逆定理的深刻刻画,是研究的一个热点和难点,其代表性工作可见文献[8-9].之后,许多学者对强逆不等式进行了深入研究和拓展.例如文献[10-11]拓 展 到 了 Bernstein型 算 子,文 献[12-14]分别研究了 Baskakov型算子和Beta算子,文献[15-18]讨论了 Szasz型算子,文献[19-20]进一步分别研究了Szasz-Mirkjan算子和Gamma算子加权逼近的强逆不等式,文献[21]讨论了多元Stancu算子逼近的强逆不等式.
文献[22]定义了K-泛函和二阶光滑模

1 若干引理
引理 1.1设φ2(x)=x(1+x),





于是,由 Riesz插值定理[24]即可完成引理1.3的证明.
引理 1.4设g'∈A.C.loc,且 φ2g″∈Lp[0,∞ ),对于1<p≤∞,则

证明类似于文献[23]的引理5的讨论,即可得到本引理的结论.
2 主要结果

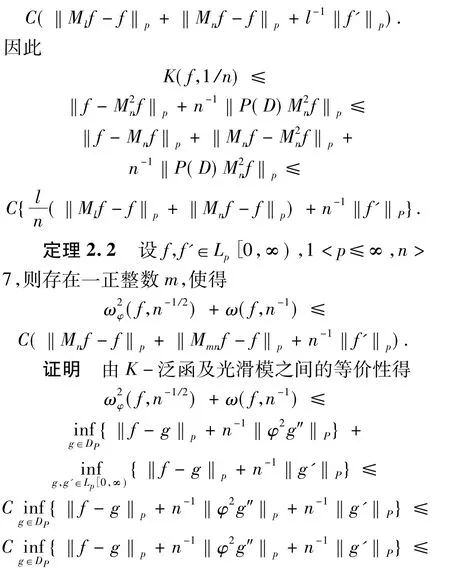

3 结语
本文讨论了一类线性正算子在Lp空间逼近的B-型强逆不等式,由此给出了该算子对可积函数类的逼近逆定理和等价刻画.有关该算子的其他逼近性质,如高维扩充[26]和饱和阶[27]仍有待于进一步研究.
[1]Agrawal P N,Thamer K J.Approximation of unbounded functions by a new sequence of linear positive operators[J].J Math Anal Appl,1998,225:660-672.
[2]Gupta V.Rate of approximation by a new sequence of linear positive operators[J].Comput Math Appl,2003,4(12):1895-1904.
[3]Gupta M K,Vasishtha V.The iterative combinations of a new sequence of linear positive operators[J].Math Comput Model,2004,39(4/5):521-527.
[4]Agrawal P N,Mohammad A J.OnLp-inverse theorem for a linear combination of a new sequence of linear positive operators[J].Soochow J Math,2006,32(3):1-13.
[5]Agrawal P N,Mohammad A J.Lp-saturation theorem for a linear combination of a new sequence of linear positive operators[J].Soochow J Math,2005,31(1):31-40.
[6]李景斌,刘国军,王式功.一类新线性正算子的Steckin-Marchaud型不等式[J].兰州大学学报:自然科学版,2008,44(6):107-111.
[7]Gupta V,Kim T,Lee S H.q-analogue of a new sequence of linear positive operators[J].J Inequal Appl,2012,144:1-9.
[8]Ditzian Z,Ivanov K G.Strong converse inequalities[J].J D'analyse Math,1993,61:61-111.
[9]Totik V.Strong converse inequalities[J].J Approx Theory,1994,40(1):369-375.
[10]李松.关于Bernstein型算子的强逆不等式[J].数学学报,1997,40(1):106-121.
[11]封梅,李翠香,吕春先.关于Bernstein-Kantorovich算子的强逆不等式[J].河北师范大学学报:自然科学版,2009,33(3):285-289.
[12]马月梅,刘国军.Lupas-Baskakov型算子逼近的强逆不等式[J].黑龙江大学学报:自然科学版,2014,31(1):51-56.
[13]齐秋兰.广义Baskakov型算子的强逆不等式[J].纯粹数学与应用数学,2002,18(4):317-321.
[14]刘丽霞,孙梅青,许景彦.关于Beta算子的强逆不等式[J].河北师范大学学报:自然科学版,2004,28(3):224-227.
[15]Qi Q L,Zhang Y P.Strong converse inequalities for certain mixed Szasz-Beta operators[J].Chin Quart J Math,2011,26(1):152-158.
[16]李松.关于Szasz-Kantorovich算子的强逆不等式[J].数学杂志,1996,16(2):137-142.
[17]刘国军,薛银川.Szasz-Durrmeyer算子逼近的强逆不等式[J].华中师范大学学报:自然科学版,2006,40(4):24-27.
[18]Yang R Y,Xiong J Y,Cao F L.Strong converse inequality for modified Szasz operators[J].J Math Res Exp,2004,24(3):437-444.
[19]Liu G J,Xue Y C,Sun W B.Strong converse inequalities for Szasz-Mirkjan operators with weights[J].Chin Quart J Math,2008,23(3):384-389.
[20]齐秋兰,郭顺生,黄苏霞.Gamma算子在空间带权同时逼近的强逆不等式[J].数学物理学报,2008,A28(3):537-545.
[21]丁春梅.多元Stancu多项式的强逆不等式[J].数学学报,2009,52(4):141-148.
[22]Ditzian Z,Totik V.Moduli of Smoothness[M].New York:Springer-Verlag,1987:1-179.
[23]丁春梅.Baskakov-Durrmeyer型算子的强逆不等式[J].信阳师范学院学报:自然科学版,1999,12(1):8-13.
[24]Riesz M.Sur les maxima des formes bilinearires et sur les fonctionnelles lineaires[J].Acta Math,1926,49:465-497.
[25]Heilmann M.Direct and converse results for operators of Baskakov-Durrmeyer type[J].Approx Theory Appl,1989,5(1):105-127.
[26]徐艳艳,陈广贵,雷文慧.利用Gaussian核对多元函数的近似逼近及其误差估计[J].四川师范大学学报:自然科学版,2009,32(5):581-587.
[27]王小刚.二元Marcinkiewicz型和的最佳逼近[J].四川师范大学学报:自然科学版,2010,33(3):306-311.

