带极点约束离散广义分段仿射系统的H∞保性能控制
王茂,周振华,王学翰
(1.哈尔滨工业大学空间控制与惯性技术研究中心,黑龙江 哈尔滨150000;2.大庆油田电力集团燃机电厂,黑龙江 大庆230604)
目前,具有范数有界时变参数不确定性广义分段仿射系统的鲁棒稳定性问题越来越受到人们的关注[1-3],但关于二次D-稳定性的研究确少有报道。为使这样的系统不但具有鲁棒稳定性,同时也需要满足某些性能指标[4],二次型性能指标提出的主要思想是对具有参数不确定性的系统设计一个控制律,不仅使得闭环系统渐进稳定,而且使得闭环系统的性能不超过某个给定的性能上界[5-7]。
随着广义分段仿射系统鲁棒控制问题研究的深入,对其进行保性能控制的研究也相继取得了一些成果[8-10]。然而,目前这方面的研究大多局限于连续系统,而所采用的方法主要是基于分段Lyapunov函数法以及一些相应线性矩阵不等式的处理方法[11-13]。王茂等研究了一类具有参数不确定离散广义分段仿射系统的静态输出反馈控制问题[14],通过求解一组包含参变量的LMIs得到保证广义分段仿射系统容许的反馈控制器增益。本文基于分段Lyapunov函数,投影定理以及几个基本引理,在前人的基础上引入带极点约束H∞保性能控制方法对离散广义分段仿射系统设计一个鲁棒H∞静态输出反馈保性能控制器。
文章的研究对象是一类具有时变参数不确定性的离散广义分段仿射系统,且不确定性体现为范数有界,本文特点在于将二次D-稳定性与H∞性能指标同时进行考虑,使得由控制器构成的闭环系统具有二次D-稳定性,且同时满足鲁棒H∞性能指标以及预先给定的二次型性能指标。
1 系统描述及预备知识
本文的研究对象是一类参数不确定性体现为范数有界形式的离散时间广义分段仿射系统:
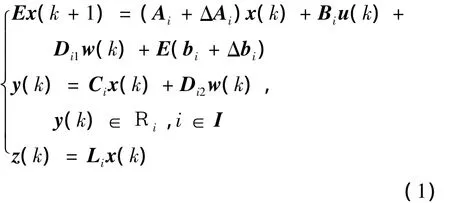
式中:x(k)∈Rnx为系统状态变量;u(k)∈Rnu为控制输入向量;y(k)∈Rny为系统输出向量;z(k)∈Rnz为可控输出向量;w(k)∈Rnw,w(k)∈l2[0,∞)为扰动输入;Ri代表第i个子系统多面体区域,Ai、Bi、Ci、Di1、Di2、Li、bi、E为第i个子系统的已知定常系数矩阵;Ebi是偏置项;索引集合是I={1,2,…,N};E∈是广义矩阵,且rank(E)=r≤nx;ΔAi和Δbi代表系统的不确定项,且满足如下形式:

式中:Wi1、Ei1和Ei2是已知的实定常矩阵,且具有适当维数,Δi(t):Z+→Rs1×s2是一个未知实值矩阵函数,且该时变矩阵函数包含Lebesgue可测量元素,具有如下形式;
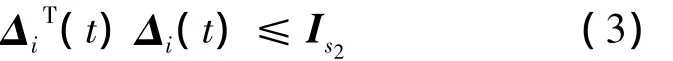
如果式(2)和式(3)成立,则称系统具有容许的参数不确定性。
将系统从多面体区域Ri过渡到Rj的集合用Ω表示,可以描述为
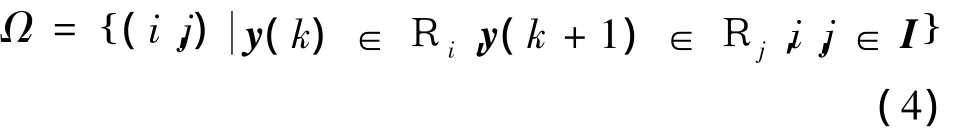
本文假设多面体区域Ri,i∈I具有形式:
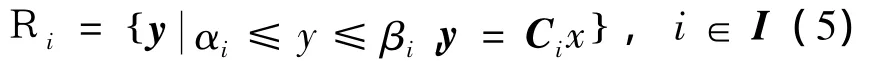
该多面体区域可进一步描述为一个椭圆集合,其中
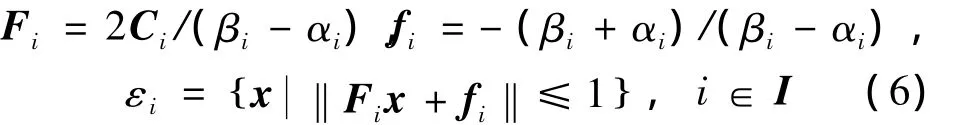
对于每个椭圆区域,可以得到
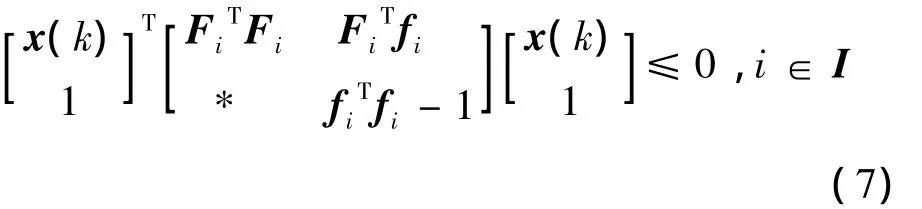
进一步将状态空间分为两类区域I=I0∪I1,I0代表包含原点的-1≤0索引集合区域,则其余的索引集合区域用I1表示。
定义1[15]考虑参数不确定广义分段仿射系统式(1),其中u(k)=0;
1)如果存在z∈C使得det(zE-Ai)≠0,则称广义系统(1)是正则的,i∈I;
2)如果 deg(det(zE-Ai))=rank(E),i∈ I则称广义系统(1)是因果的;
3)如果离散广义系统(1)的所有特征根λ(E,Ai)⊂Dint(0,1),则称系统(1)稳定;
4)如果系统(1)是正则、因果,并且稳定的,则称广义系统(1)是容许的;
5)任意非零向量ν1,若满足Eν1=0,则称其为矩阵束 (E,Ai)的一阶向量,对于满足 Eνk=Aiνk-1的非零特征向量νk(k≥2),则称为矩阵束(E,Ai)的k阶特征向量。
以下定义2和定义3,所考虑广义系统一般形式为
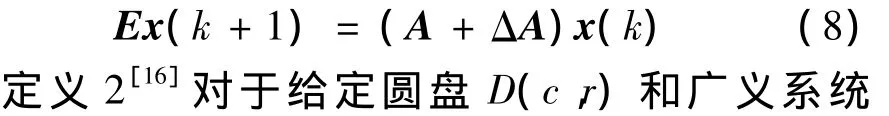
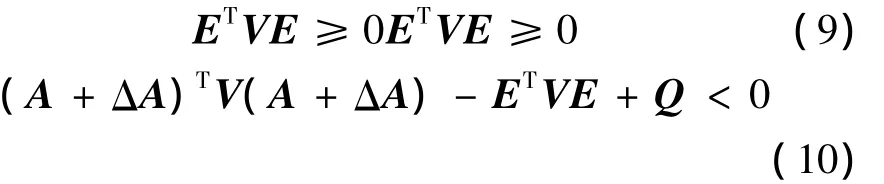
则称V为广义系统(8)的一个二次性能矩阵,相应的闭环性能指标值J≤Vx0。x0为系统初始状态。
定义3[16]对于给定圆盘 D(c,r),广义系统式(8)若存在对称可逆矩阵T,对所有的ΔA,对称可逆矩阵T满足式(9)以及:
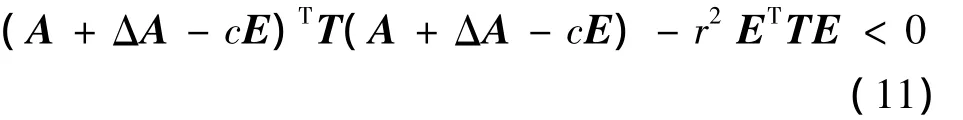
则称广义系统式(8)是二次D-稳定的。若对称可逆矩阵T同时满足式(9)和式(11),则称对称可逆矩阵T为广义系统式(8)的一个二次D-性能矩阵。
引理1 对于适当维数实矩阵M=MT、S、N和Θ(t),若满足ΘT(t)Θ(t)≤I,则当且仅当存在某个标量ε>0,使M+SΘ(t)N+NTΘT(t)ST<0等价于M+εSST+ε-1NTN <0。
应用shcur补引理,M+εSST+ε-1NTN <0可以进一步表述为以下2种形式:
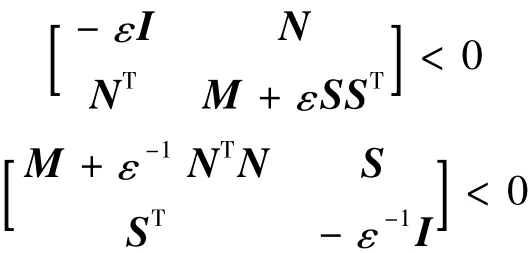
引理2[17](投影定理) 给定矩阵h=hT∈Rn×n,u∈Rk×n和v∈Rm×n,则关于变量Φ的矩阵不等式h+uTΦTv+vTΦu<0是LMI可解的,当且仅当:
1)若 v⊥=0,u⊥≠ 0,则 uT⊥hu⊥< 0
2)若 u⊥=0,v⊥≠ 0,则 vT⊥hv⊥< 0
3)若 u⊥≠0,v⊥≠0,则 uT⊥hu⊥< 0,vT⊥hv⊥<0同时成立,u⊥,v⊥代表u和v的右正交核空间。
本文针对具有参数不确定性离散时间广义分段仿射系统式(1)设计H∞输出反馈保性能控制器:
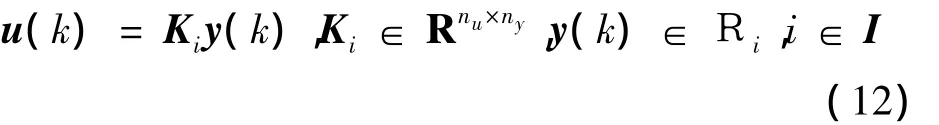
保证闭环系统:
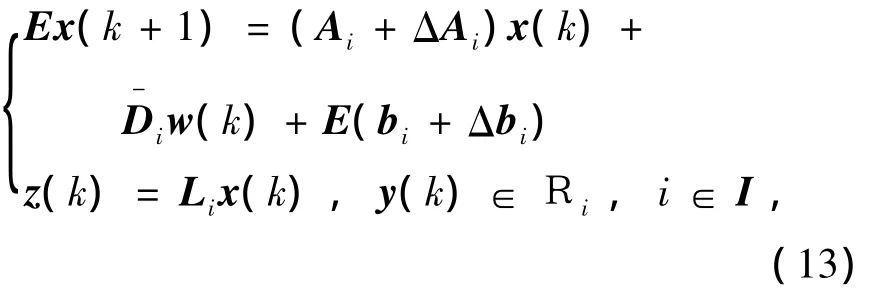
式中系统状态矩阵:Ai=Ai+BiKiCi,扰动矩阵:=Di1+BiKiDi2)是容许的,且具有二次D-稳定性,满足性能指标:
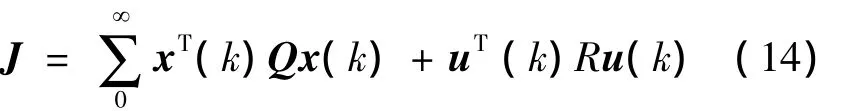
式中:Q、R为已知正定加权矩阵。
2 主要结果
假设系统式(1)的输入矩阵Bi,i∈I是列满秩的,则存在一组转换矩阵 TBi∈ Rnx×nx,i∈ I ,满足:
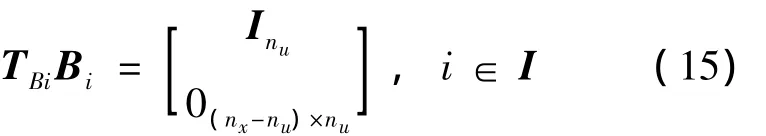
且转换矩阵 TBi∈Rnx×nx非奇异,以下 H∞静态输出反馈保性能控制器就是基于该假设进行设计的。
定理1 考虑参数不确定离散广义分段仿射系统(1),若存在对称矩阵 Pi∈ Rnx×nx,标量:
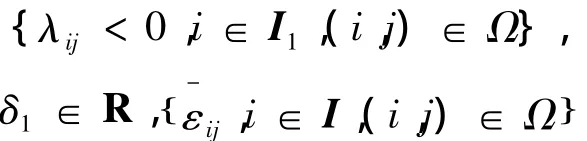
以及:
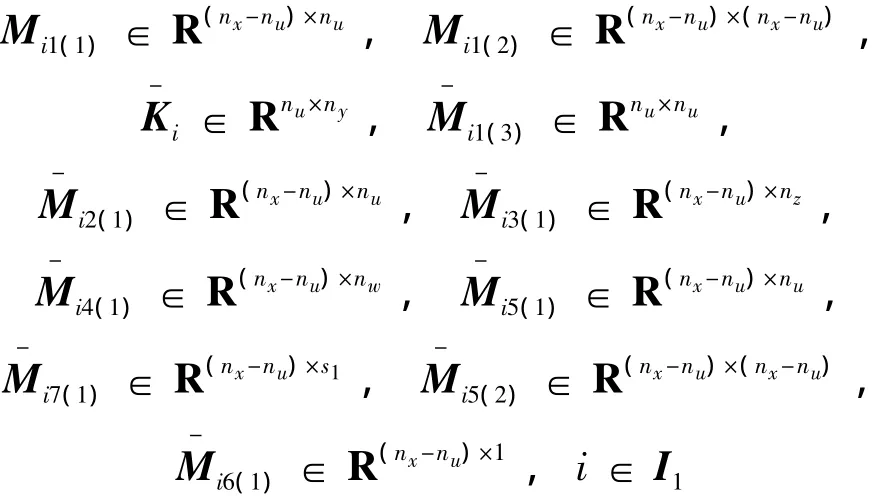
使得

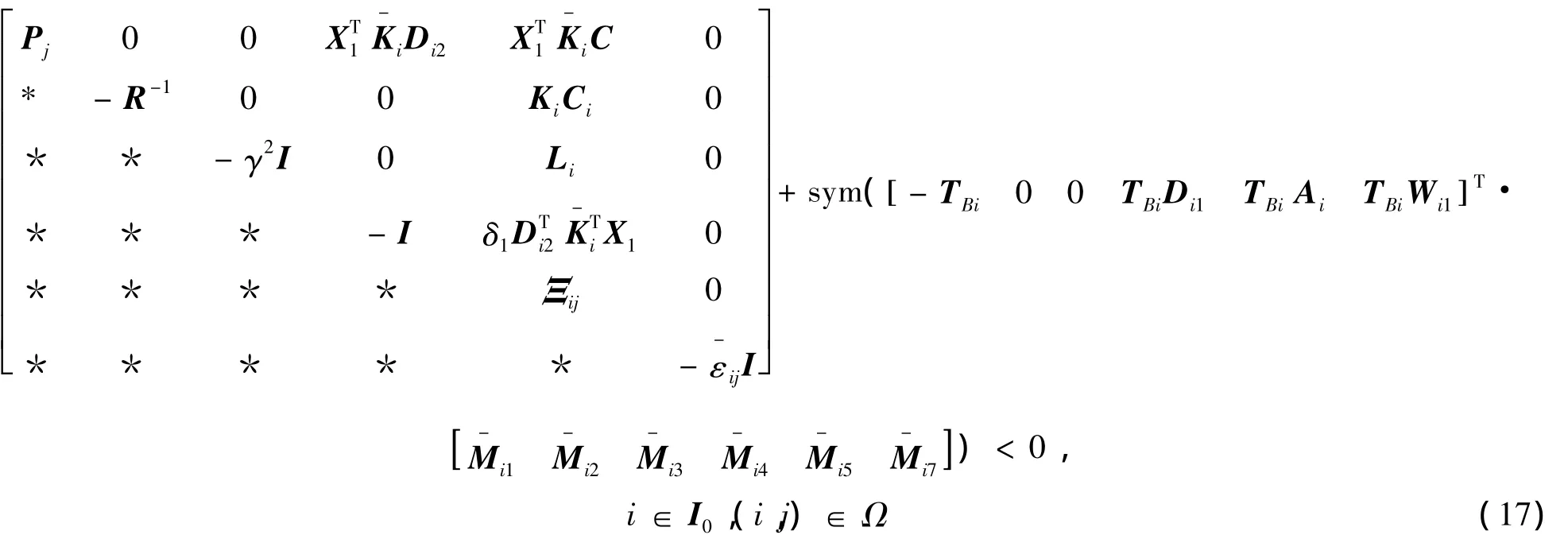
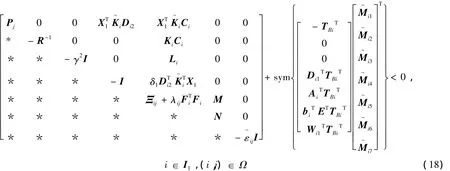
成立,则存在H∞输出反馈保性能控制器式(12),使得闭环系统式(13)是容许的,且满足二次性能指标式(14),即Pi∈Rnx×nx为闭环系统式(13)的一个二次性能矩阵。
对任意矩阵H,sym{H}=H+HT。

H∞输出反馈保性能控制器增益:
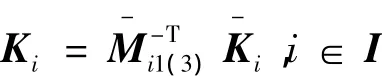
证明:可以看到条件式(18)在Ebi=0时,就是条件式(17)。不失一般性,如下可以只证明条件式(18)成立。
选取广义分段仿射Lyapunov函数:
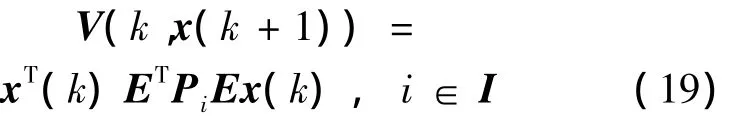
进一步:
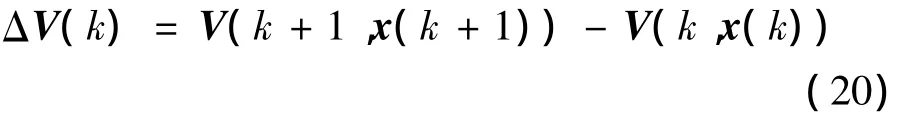
基于Lyapunov函数的定义,为使闭环系统式(13)具有鲁棒H∞性能指标γ,则只需保证以下不等式成立:
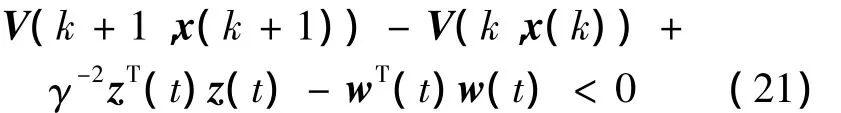
对于闭环系统式(13),根据定义2关于二次性能矩阵的定义,如果下面不等式成立,则系统具有H∞二次保性能矩阵Pi:
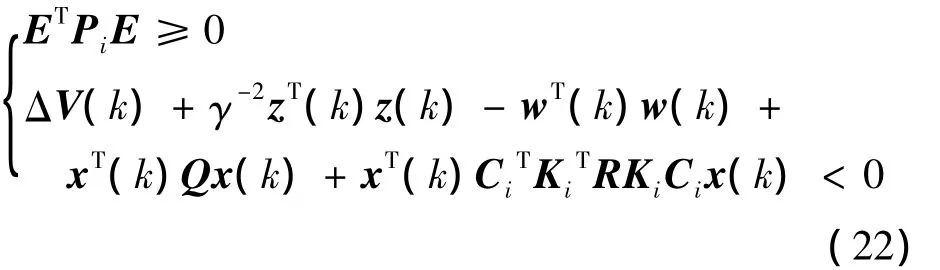
对于任意非零w(k)∈l2[0,∞),式(22)可进一步等价于:
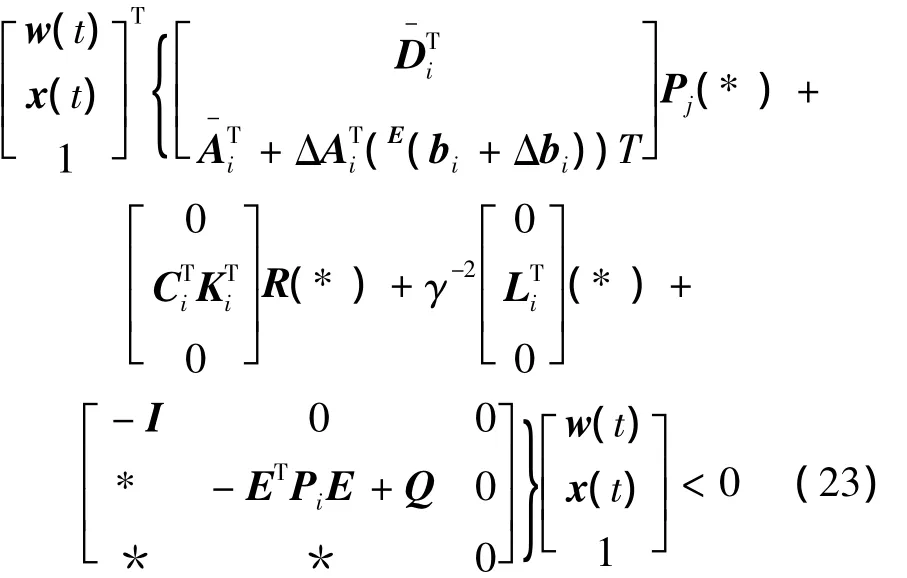
从式(23)可以得到:
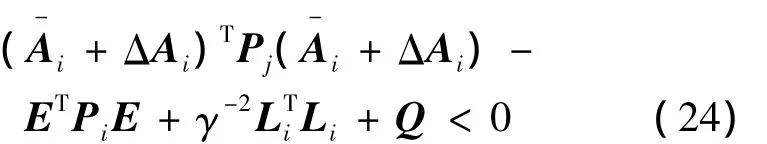
即
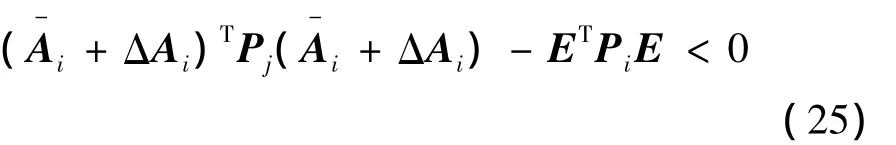
假设矩阵束(E,Ai)是非因果的。用一阶特征向量ν1和它的Hermitian矩阵ν1*分别左乘和右乘式(25)得
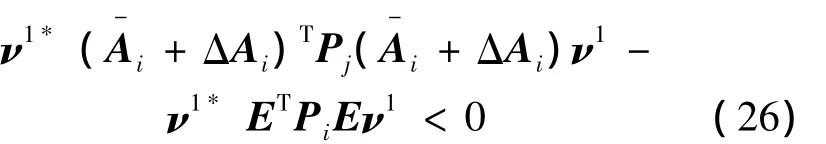
接下来引用schur补引理,再用Eν2代替Aiν1,并注意到Eν1=0,可以得到
与条件式(16)相矛盾。所以得到矩阵束(E,Ai)是因果的。显然,证明因果性的同时也证明了矩阵束(E,Ai)的正则性。
考虑区域信息,即将式(7)代入式(23)并应用 S-procedure,其中 λij< 0,i∈ I1,(i,j)∈ Ω ,得到

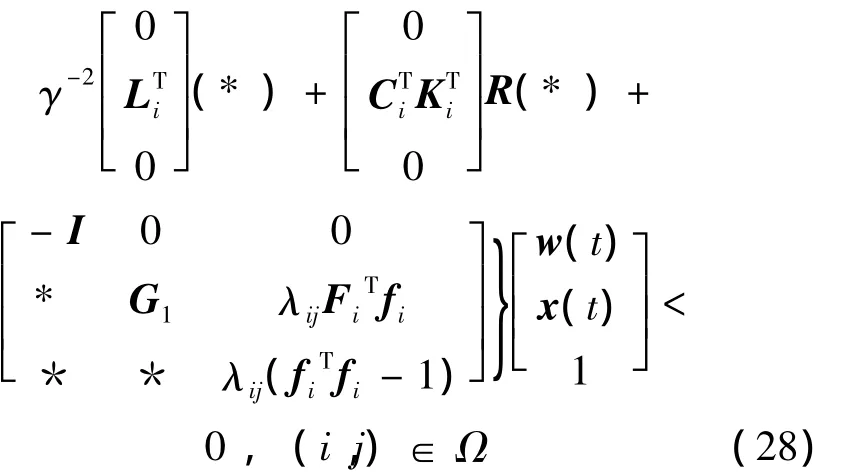
式中:G1=-ETPiE+λijFiTFi+Q。对式(28)中各个矩阵进行合并,并先后应用3次Schur补引理,从式(28)可以得到
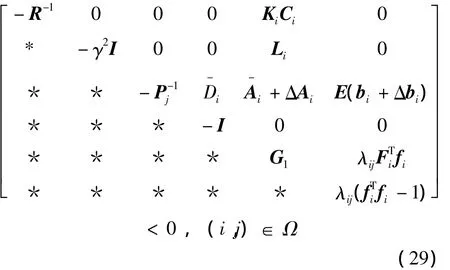
另一方面,为消除不确定性给求解过程带来的影响,将式(29)中的不确定性ΔAi和EΔbi分离出来,可以将式(29)改写为
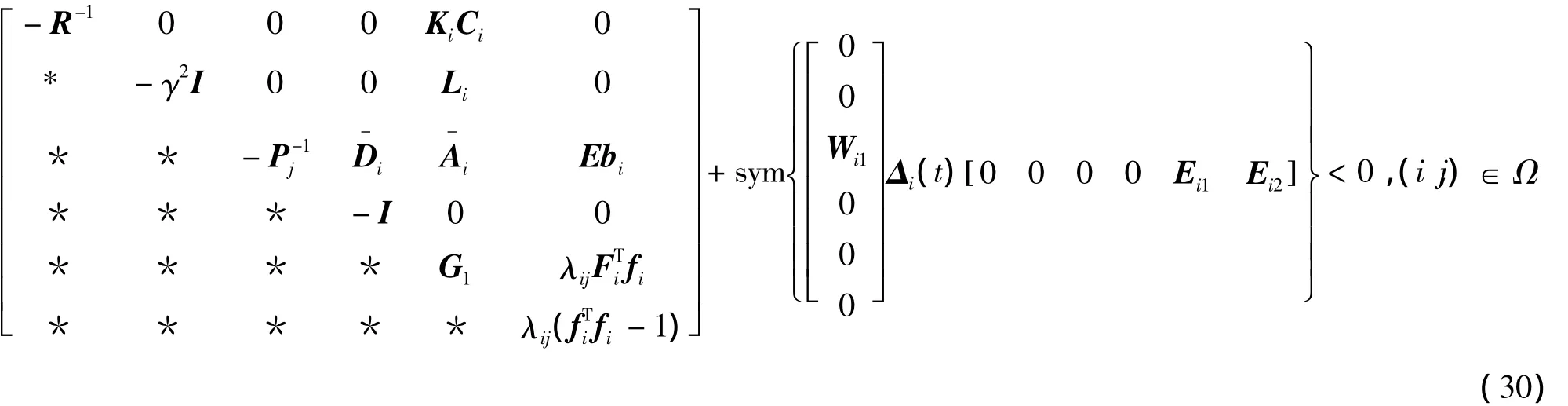
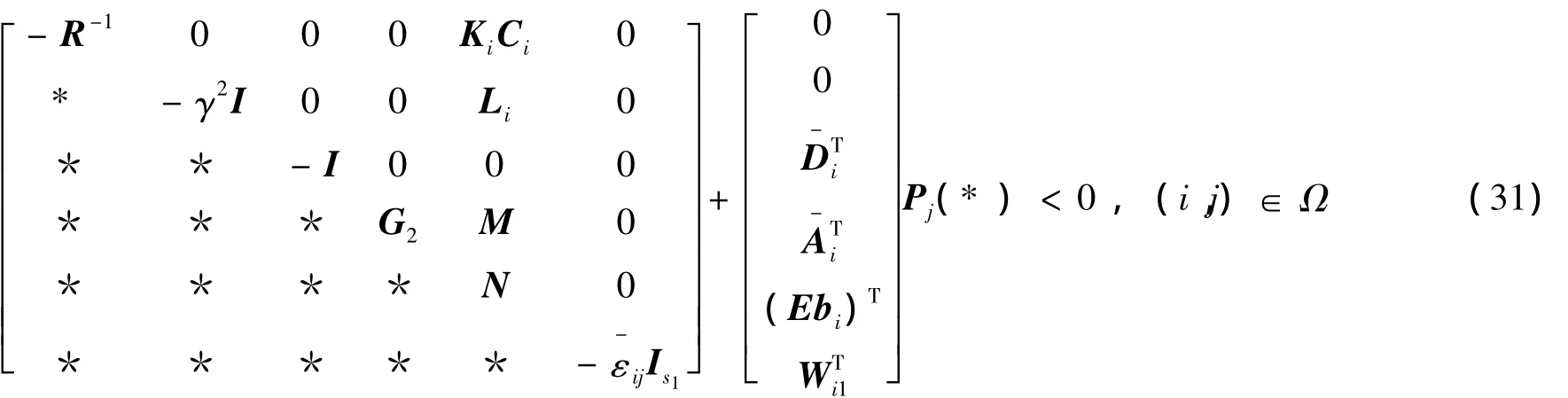
式中,G=-ETP E+λF+E+Q。系
2
iiji1统矩阵与Lyapunov矩阵相耦合。因此以下应用投,(31)影定理消去这种耦合关系 将式 改写成为

基于投影定理,做如下变量替换:
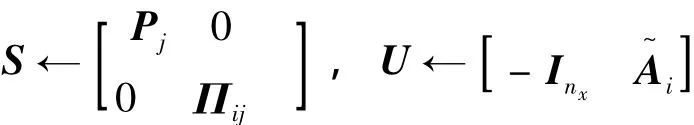
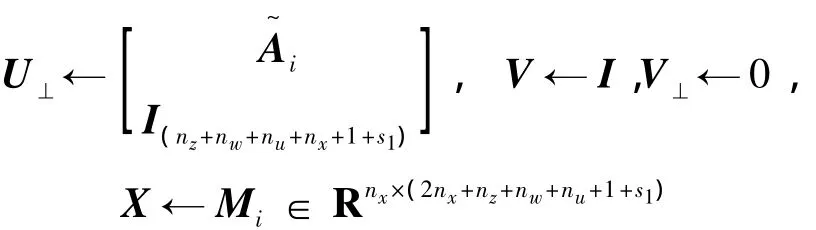
应用引理2的投影定理,得到
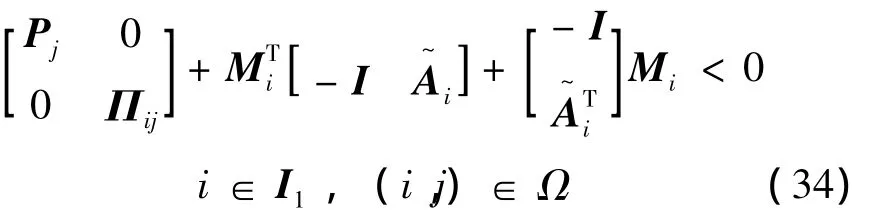
对矩阵 Mi∈ Rnx×(2nx+nz+nw+nu+1+s1),i∈ I1进行分块:
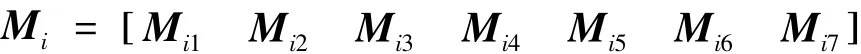
其中:
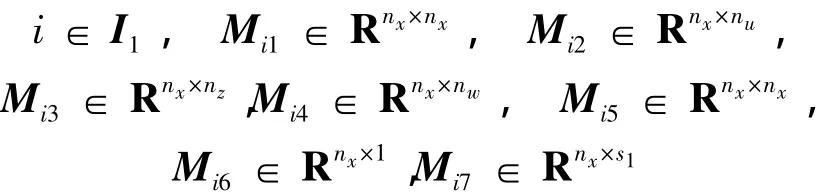
相应矩阵的定义与定理1中给出的形式一样。结合变量δ1:
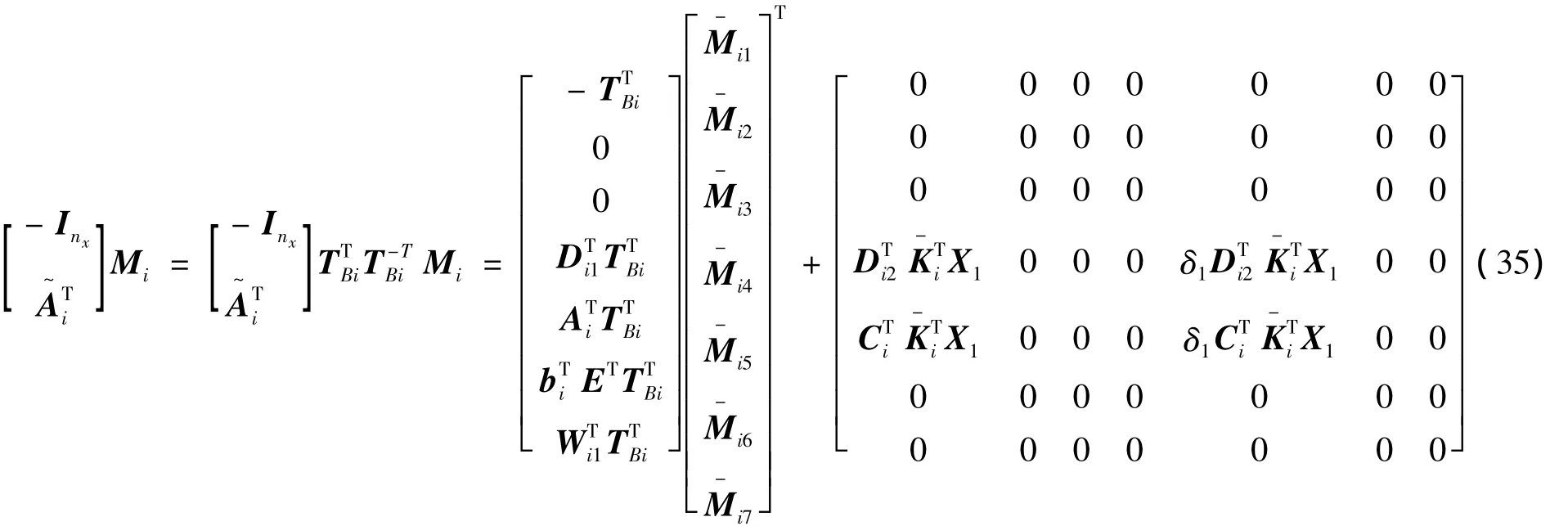
将式(35)代入到式(34)中,并结合所有给定矩阵的定义,最终得到式(18),第一部分证明结束。
另一方面,从式(17)、(18)可以得到
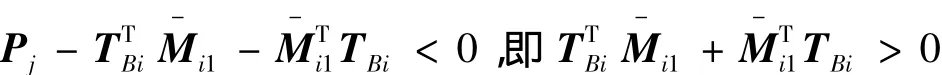
--性,并且由 Mi1是下三角阵,可以得到 Mi1(3)可逆。所以控制器增益能够得到,定理进一步证明完毕。
定理2 考虑范数有界离散广义分段仿射系统式(1),若存在对称矩阵 Pi∈ Rnx×nx,标量:
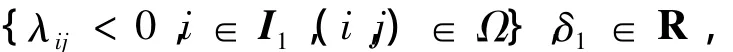
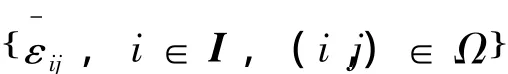
以及
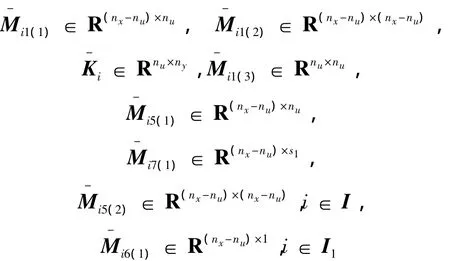
使得式(16)~(18)成立,且满足以下不等式:
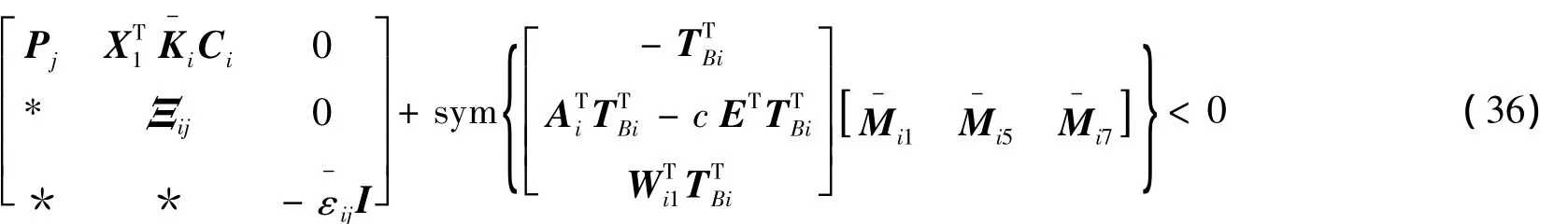

则存在H∞静态输出反馈保性能控制器式(12),使得闭环系统式(13)具有二次D-稳定性,且对于所给二次型性能指标式(14),Pi为一个二次D-性能矩阵。则闭环系统式(13)的控制器增益:
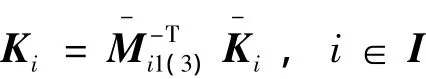
闭环系统式(13)相应的性能上界为
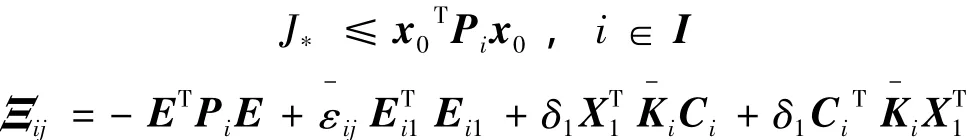
证明 首先,由定义3可知,若一般形式广义系统式(8)是二次D-稳定的,则存在对称可逆矩阵Pi必须同时满足以下2个不等式:
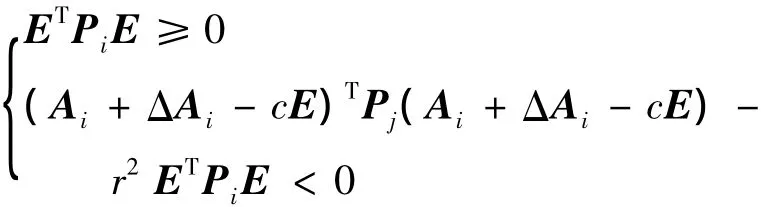
第1个不等式与条件式(16)相同,第2个不等式也等价于:
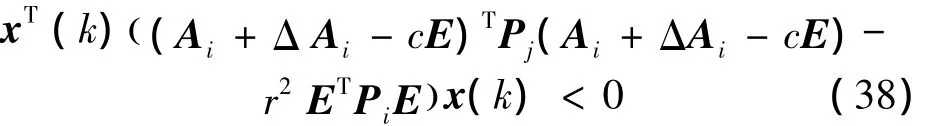
推广到本文所考虑的离散广义分段仿射系统式(1),若使系统式(1)是二次D-稳定的,只需满足条件式(16)以及以下不等式:
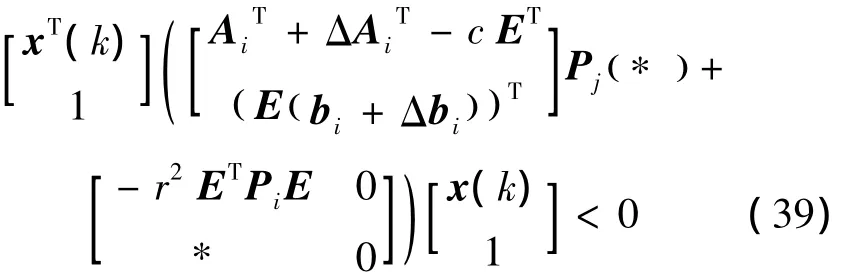
考虑区域信息,将式(7)代入式(39)中,并且应用S-procedure引理,即可得:> 0
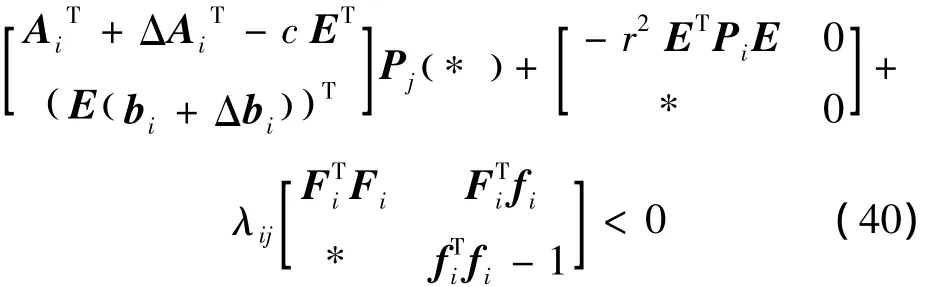
基于定理2,引入一组标量 ,i∈ I1,(i,j)∈Ω,并引用schur补引理,不等式:
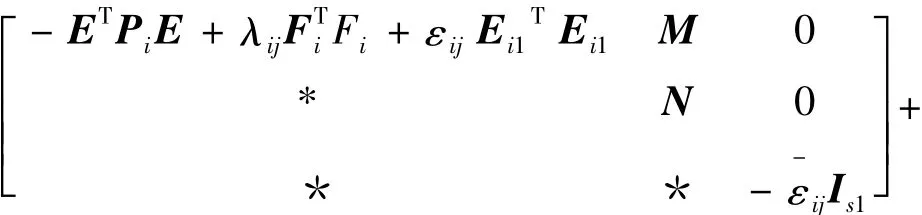
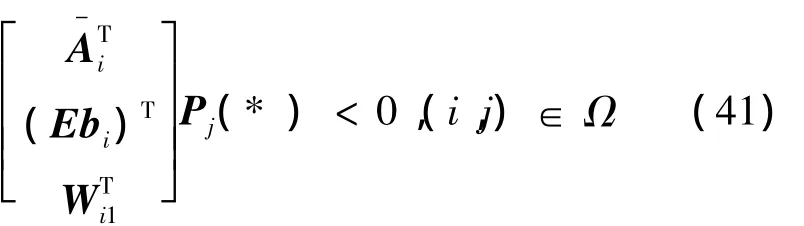
与式(40)等价,其中M和N的定义见定理1。
以下证明方法与定理1相同,去掉系统矩阵和Lyapunov矩阵的耦合关系之后,即可得到条件式(36)、(37)。显然,根据定理 1,由于 Pi满足式(16)、(18),则Pi为闭环系统式(13)的一个二次性能矩阵,而Pi又满足式(36)、(37),所以Pi为闭环系统式(13)的一个二次D-性能矩阵,定理2得证。
3 数值仿真
由于本文所考虑离散广义分段仿射系统存在外部扰动输入,应用定理1设计得到的控制器,应使得由此构成的闭环系统式(13)具有鲁棒H∞性能,且满足预先给定的二次型性能指标。然而,基于定理2设计控制器的主要思想则是考虑将闭环系统式(13)的极点配置在所期望的位置上,以保证系统具有实际工程中所要求的动态和稳态性能,与此同时,闭环系统式(13)还应满足一定的H∞性能指标和二次型性能指标。
考虑参数不确定性体现为范数有界形式的离散广义分段仿射系统式(1)由以下2个子系统组成:
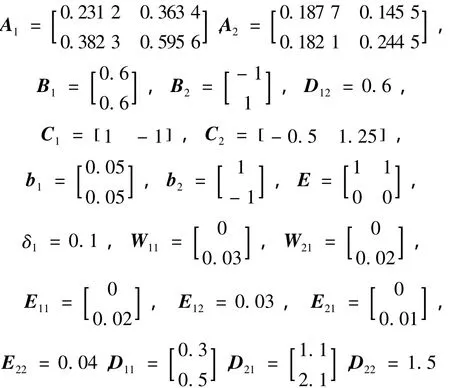
椭圆体系数矩阵:
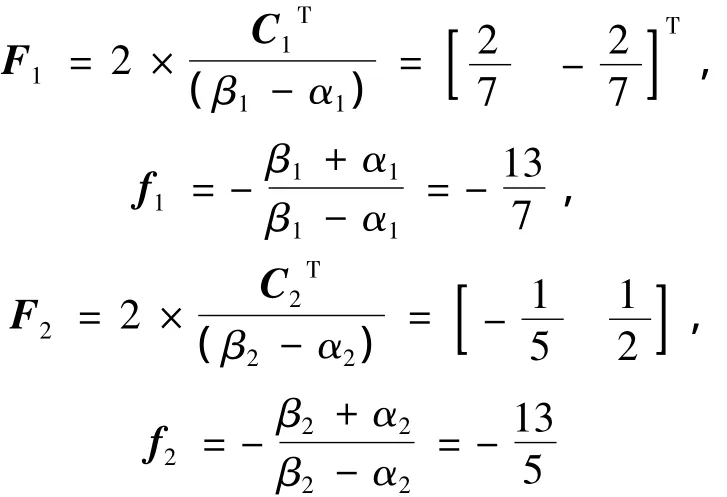
式中:α1=3,β1=10,α2=4,β2=9 ,R=5,Q=。系统初始状态x0=[1 1]T系统扰动输入向量w =[2 1]TL1= [0.1 0.2 ],L2=[0.3 0.4 ]圆盘 D(c,r):c1=-5,c2=-10,r1=5,r2=10应用定理1得到闭环系统式(13)的一个二次性能矩阵以及使闭环系统式(13)容许的H∞静态输出反馈保性能控制器增益:
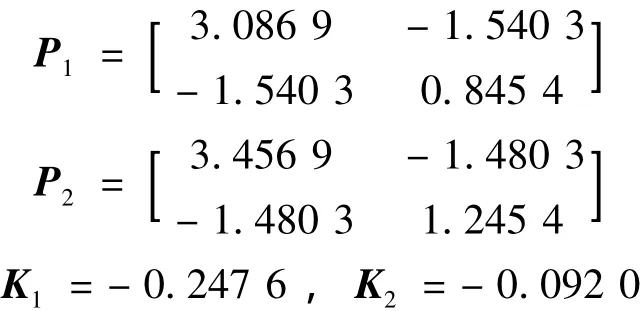
H∞性能指标γ=6.902 5。相应得到系统的一个性能上界:J*≤0.851 7。
图1为根据定理1得到的H∞输出反馈保性能控制器所构成闭环系统式(13)的状态响应曲线:

图1 根据定理1得到的系统状态响应曲线Fig.1 State responses of the closed-loop system according to lemma 1
应用定理2得到使闭环系统式(13)具有二次D-稳定性的一个二次D-性能矩阵以及使闭环系统式(13)容许的H∞静态输出反馈保性能控制器增益:H∞性能指标γ=13.563。相应得到系统的一个性能上界:J*≤7.041。
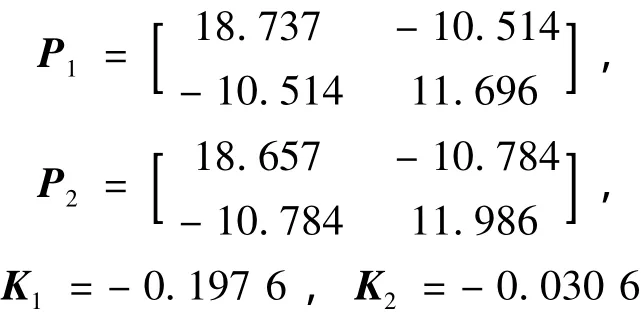
图2为根据定理2得到的H∞输出反馈保性能控制器所构成闭环系统式(13)的状态响应曲线。

图2 根据定理2得到的系统状态响应曲线Fig.2 State responses of the closed-loop system according to lemma 2
由通过仿真所得到的数据可以看到,基于定理1所设计的控制器使得闭环系统式(13)H∞扰动抑制度γ=6.902 5,且性能上届小于0.851 7,满足先前的设计要求。基于定理2所设计的控制器使得闭环系统式(13)具有二次D-稳定性,同时得到系统的H∞干扰抑制度 γ=13.563,相应性能上届为7.041。通过分析可以看到,基于定理2的控制器设计方法由于考虑了系统的二次D-稳定性使得H∞性能指标较基于定理1所得到的同类性能指标有所下降,即:闭环系统式(13)具有二次D-稳定性时鲁棒性能有所下降。
下面采用一个实际例子进行说明,使用隧道二极管电路作为一个物理映射,证实对范数有界广义分段仿射系统H∞静态输出反馈保性能控制器的求取[14],定理1比定理2具有更好的系统鲁棒控制性能,考虑隧道二极管电路[18],电容电压用x1(k)表示,电感电流用x2(k)表示,流过隧道二极管的电流用x3(k)表示。经过离散化得到离散广义分段仿射系统模型:系统参数的取值参看文献[14],其余参数及椭圆区域分段按照第一个数值例子进行选择,系统扰动输入向量
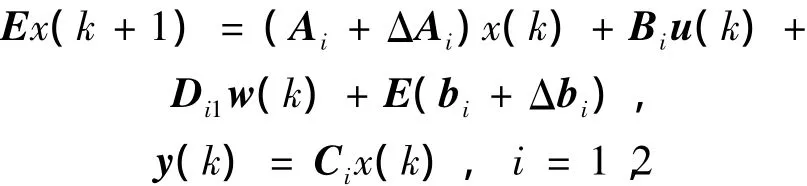
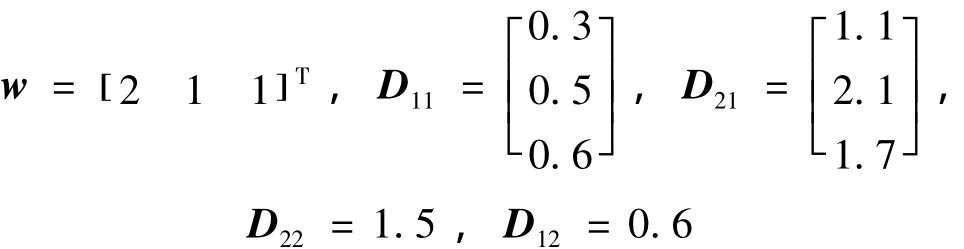
进行实验仿真可得:基于定理2求取H∞静态输出反馈控制器时,利用Matlab软件无法得到可行解。基于定理1求取广义分段仿射系统H∞静态输出反馈保性能控制器增益:K1=-1.256 6,K2=-0.526 3。H∞性能指标γ=9.563。
从仿真所得数据可以看到基于定理2的控制器设计方法由于考虑了二次D-稳定性使得闭环系统鲁棒性能有所下降。
4 结束语
本文在分段仿射Lyapunov函数,投影定理以及几个处理线性矩阵不等式基本引理的基础上,设计了使具有范数有界形式参数不确定性的离散时间广义分段仿射系统容许的H∞输出反馈保性能控制器,保证了由此构成的闭环系统具有二次D-稳定性。控制器存在的充分条件在所采用算法的基础上最终体现为LMIs约束的形式,并且求解过程不包含对系统矩阵的分解,这种做法大大减低了算法的保守性,最后的数值仿真给出了H∞静态输出反馈保性能控制器的最优解,同时使得闭环系统极点被约束在复平面指定区域上,并注意到由于考虑系统的二次D-稳定性使得系统原本H∞性能指标有所下降。仿真证明了设计方法的有效性。
[1]MASUBUCHI,KAMITANE Y,OHARA A.H∞control for descriptor systems:amatrix inequalities approach[J].Automatica,1997,33(4):669-673.
[2]De OLIVEIRA M C,GEROMEL JC.A class of robust stability conditions where linear parameter dependence of the Lyapunov function is a necessary condition for arbitrary parameter dependence[J].Systems Control Letters,2005,54:1131-1134.
[3]QIU J,FENG G,GAO H.Approaches to robust H∞static output feedback control of discrete-time piecewise-affine systems with norm-bounded uncertainties[J].Int J Robust Nonlinear Control,2011,21:790-814.
[4]PERESP L D,GEROMEl JC.H∞guaranteed cost control for uncertain continuous-time linear systems[J].Systems and Control Letters,1993,20:413-418.
[5]DAAFOUZ J,BERNUSSOU J.Poly-quadratic stability and H∞performance for discrete systems with time varying uncertainties[C]//Proceedings of the 40th IEEE Conference on Decision and Control.Orlando,FL,USA,2001:267-272.
[6]GEROMEL JC,OLIVEIRA de M C,BERNUSSOU J.Robust filtering of discrete-time linear systems with parameter dependent Lyapunov functions[J].SIAM JControl Optim,2002,41(3):700-711.
[7]LEITE V JS,PERES P L D.An improved LMI condition for robust D-stability of uncertain polytopic systems[J].IEEE Trans Automat Control,2003,48(3):500-504.
[8]KIM JH.Delay-dependent robust and non-fragile guaranteed cost control for uncertain singular systems with time-varying state and input delays[J].International Journal of Control,Automation,and Systems,2009,7(3):357-364.
[9]REN Junsheng,ZHANG Xianku.Guaranteed cost control of nonlinear singular system with time delays using T-S Fuzzy model[J].Applied Mathematics & Information Sciences,2013,7(4):1615-1622.
[10]ZHU X L,YANGG H.Integral inequality approach to stability analysis of continuous-time systems with time-varying delay[J].IET Control Theory,2008,2(6):524-534.
[11]DONG J,YANG G H.Robust static output feedback control for linear discrete-time systems with time-varying uncertainties[J].Systems and Control Letters,2008,57(2):123-131.
[12]BARBOSA K A,SOUZA C E de.Robust H∞filtering for discrete-time with uncertainty nonlinear systems using parameter-dependent Lyapunov functions[C]//Proceedings of the American Control Conference.Alaska,USA,2002:3224-3229.
[13]DONG J,YANG G H.Static output feedback control synthesis for linear systems with time-invariant parametric uncertainties[J].IEEE Transactions on Automatic Control,2007,52(10):1930-1936.
[14]WANG Mao,WEI Yanling,QIU Jianbin.Static output feedback control of discrete-time piecewise affine singular systems[J].Journal of Harbin Institute of Technology,2013,45(3):14-21.
[15]HSIUNG K L,LEE L.Lyapunov inequality and bounded real lemma for discrete-time descriptor systems[J].IEEE Proc-Control Theory,1999,146(4):327-331.
[16]杜宝珠.不确定广义系统的保性能控制[D].沈阳:东北大学,2006:37-40.DU Baozhu.Guaranteed cost control for uncertain singular systems[J].Shenyang:Northeastern University,2006:37-40.
[17]BOYD S,EL G L,FERON E,et al.Linearmatrix inequality in systems and control theory[M].SIAM:Philadelphia,PA,1994.
[18]RODRIGUES L,BOYD S.Piecewise-affine state feedback for piecewise-affine slab systems using convex optimization[J].Systems and Control Letters,2005,54(9):835-853.

