素数幂次本原置换群的一个简明刻画＊

蔡迁 张华

（1.普洱学院 教师教育学院，云南 普洱665000；2.云南师范大学 数学学院，云南 昆明650500）

1 引 言

传递置换群的研究，特别是本原置换群的研究，长期以来受到许多群论学者的关注.由于一般的传递置换群数量庞大，在对其进行研究时，常需要对其次数做一定的限制.早在1832年，Galois就证明了仿射线性群PSL2（p）在素数p个（p＝5，7，11）点上的本原置换表示.1861年，Mathieu发现了两个著名的素数次置换单群M11和M23.1901年Burnside分类了所有的素数次传递置换群，并且证明了这类群要么是2－传递，要么包含一个正规正则p－子群［1］.1981年，单群分类定理的问世，使得人们知道了所有的2－传递置换群［2］，由此很容易得到Burnside的结果［3］.紧接着在1983年，包含一个指数为素数幂的子群的非交换单群被Guralnick完全刻画［4］.工作还在继续，1985年，Liebeck和Saxl分类了奇数次本原置换群［5］.Li C H 和Serres在2003年确定了非平方元次本原置换群［6］.紧接着，Li C H确定了2·3r、5·3r和10·3r（r为素数）次本原置换群［7］.

关于特殊次本原置换群的研究，Gareth A.Jones于1975年在他的博士论文中首次研究了素数幂次本原置换群.由于在当时还没有单群分类定理，所以对素数幂次本原置换群还很难给出完整的分类.1976年，Praeger也研究了素数幂次本原置换群［8］.

2002年，Dobson确定了p2次Sylow p－子群不同构于ΖpwrΖp所有传递置换群［9］.因此很自然的可以提出如下问题：研究p3次传递置换群，或者更一般地：研究素数幂次传递置换群.作为这个问题的第一步，是研究本原的情形.由著名的O′Nan－Scott定理，素数幂次本原置换群的类型是知道的，但是缺乏一个简明清晰的刻画.

本文工作是Burnside定理和Dobson工作的继续，主要针对本原的情形给出除仿射型外的素数幂次本原置换群的一个清晰的刻画.

本文的主要结果如下：

定理1 假设G是Ω上的本原置换群，且｜Ω｜＝pn，p是一个素数，n≥2.则下述之一成立.

（Ⅰ）G是2－传递的.

（1）G是HA型本原群，并且G＝Ζn∶Gα≤AGLn（p），其中Gα≤GLn（p）作用在向量空间V＝的非零向量上是传递的.

（2）G是AS型本原群，并且G＝或者PSLk（q）≤G≤PΓLk（q），其中（qk－1）／（q－1）＝pn.

（Ⅱ）G不是2－传递的，且下述之一成立.

（1）G是 HA型本原群，并且G＝：Gα≤AGLn（p），其中Gα≤GLn（p）是不可约的，且作用在向量空间V＝的非零向量上不传递.

（2）G是AS型本原群，并且G＝PSU4（2）≅PSp4（3），或者PSU4（2）.2≅PSp4（3）.2，其中p＝n＝3.

（3）G是PA型本原群，并且Td＝soc（G）◁G≤UwrK，其中1＜d≤n，d｜n，且K≤Sd传递，soc（U）＝T≤为下述之一：

；PSLk（q），其中（qk－1）／（q－1）＝pn／d；M11，其中p＝11，n＝d；PSL2（11），其中p＝11，n＝d；M23，其中p＝23，n＝d；PSU4（2），其中1＜d＝n／3.

注1 群GLn（p）中的所有作用在向量空间V＝Ζnp的非零向量上传递的子群被Hering确定［10］.

2 预备知识

假设Ω是任意有限非空集合，Ω到Ω自身的一个一一映射，称为一个置换.Ω上的全体置换构成一个群，称为Ω上的对称群，记为Sym（Ω）.如果G≤Sym（Ω），就称G是Ω上的置换群，通常也称G是｜Ω｜次置换群.

对于某个点ω∈Ω，群G中所有保持点ω不变的元素组成G的一个子群，称为群G的点稳定子群，记为Gω，即Gω＝｛g∈G｜ωg＝ω｝.而把群G作用在非空集合Ω上的轨道定义为：由非空集合｛ωg｜∀g∈G｝所组成的集合，记为ωG.对于群的阶，轨道长度与点稳定子群三者之间的关系如下：引理1 设G是Ω上的置换群，则对任意的点ω∈Ω，存在轨道ωG到［G∶Gω］一个映射，并且｜ωG｜＝｜G∶Gω｜＝｜G｜／｜Gω｜.特别地，如果G是传递的，则｜Ω｜＝｜G∶Gω｜，或者｜G｜＝｜Ω｜｜Gω｜.

设群G作用在集合Ω上.如果对任意的两个点α、β∈Ω，存在元素x∈G使得β＝αx，则称G作用在Ω上是传递的.如果对于任意的点ω∈Ω都有Gω＝1，Ω上的置换群G称为半正则的.而如果Gω＝1对任意的元素ω∈Ω都成立，Ω上的传递置换群G称为正则的.

设Ω是一个集合，则集合B＝ ｛B1，B2，…，Bm｝称为Ω的一个划分，如果Bi⊆Ω，Ω＝B1∪B2∪…∪Bm，且当i≠j时有Bi∩Bj＝Ø.当｜B｜＝1或｜Ω｜时，称B为Ω的平凡划分.设G是Ω上的传递置换群，称Ω的一个划分B＝ ｛B1，B2，…，Bm｝为G－不变的，如果对于任意的元素g∈G和任意的Bi∈B，有Big∈B.

设G是Ω上的传递置换群.Ω的子集合B称为G的一个块，如果对每个元素g∈G，有Bg∩B＝Ø或者Bg＝B成立.Ω中的单点集和Ω本身显然是G的块，称为G的非平凡块.

作用在Ω上的传递置换群G称为本原的，如果G没有非平凡的不变划分.显然这等价于：G没有非平凡的块.

本原群有如下的重要性质.

引理2Ω上的传递置换群G是本原的当且仅当对任意的点α∈Ω，点稳定子群Gα是G一个极大子群.

设G≤Sym（Ω），正整数k≤｜Ω｜.称G为k重传递的（或k－传递的），如果对Ω的任意两个k元有序子集（i1，…，ik）和（j1，…，jk），存在元素g∈G使得（i1，…，ik）g＝ （j1，…，jk），即isg＝js，s＝1，…，k.

从定义可以看出高重传递性可以推出低重传递性.下面给出几个关于多重传递群的重要引理.引理3 设G是Ω上的传递群，k≥2，α∈Ω.则G在Ω上k－传递当且仅当点稳定子群Gα在Ω＼｛α｝上（k－1）－传递.

引理4Ω上的2－传递群G为本原群.

下面介绍 O′Nan－Scott定理［3，11］.

假设G是Ω上本原置换群，并且令H＝soc（G）.则H＝T1×…×Tm≅Tm.

（1）如果H是初等交换p－群Zp m，p为素数，则｜Ω｜＝pm，且G＝∶Gα≤AGLm（p），其中Gα是GLm（p）的不可约子群；此时称G为HA型（Holomorph Affine）本原群.

（2）如果H＝T为非交换单本原群，则T≤G≤Aut（T）， 此 时 称G为 AS 型 （Almost Simple）本原群.

（3）如果H≅Tm，m≥2，T为非交换单群，｜Ω｜＝｜T｜m－1，并且Hα＝ ｛（t，t，…，t）｜t∈T｝≅T.则称G为SD型（Simple Diagonal）本原群.

（4）如果H≅Tm，T为非交换单群，m≥2；G≤UwrK（同构意义下），d＜m，d｜m，其中K≤Sym（m／d）传递，U是l次AS型或者SD型本原群，soc（U）≅Td且｜Ω｜＝lm／d.此时称G为PA型（Product Action）本原群.

（5）如果H≅Tm，T为非交换单群，m≥6并且H正则作用在Ω上，此时称G为TW型（Twisted Wreath product）本原群.

定理2（O′Nan－Scott） 设G≤Sym（Ω）为本原群，则G必属下述五种类型之一：HA，AS，CD，PA，TW.

定理3（Burnside定理） 一个2－传递置换群是HA或AS型.

3 素数幂次本原置换群

对于本原置换群的研究，即便有了关于本原群结构的O′Nan－Scott定理，研究各种带特殊限制条件的本原群仍然是一个有趣而重要的问题.有了前面的一些预备知识后，本节主要讨论素数幂次本原置换群.由O′Nan－Scott定理可知，素数幂次本原置换群只能是HA、AS或者PA（见下面的命题1）.

假设G是Ω上的本原置换群，这里｜Ω｜＝pn，p是一个素数.

当n＝1时，只要G在Ω上传递，就能推出G在Ω上是本原的.下面的这个关于素数次传递群的引理是熟知的［3］.

引理5 假设G是Ω上的传递置换群，且｜Ω｜＝p是一个素数，则下述之一成立.

（1）G是 HA 型 本 原 群， 且Ζp≤G≤AGL1（p）.

（2）G是AS型本原群，并且G满足下列条件之一：

①G＝Ap或Sp；

②PSLn（q）≤G≤PΓLn（q），其中（qn－1）／（q－1）＝p；

③G＝PSL2（11）或PΓL2（11），p＝11；

④G＝M11或M23，p＝11或23.

当n＝2时，Ω上的传递置换群被Dobson和Witte［9］进行了研究.他们的分类近乎完全，特别对p2次的本原置换群按照2－传递和本原非2－传递（imprimitive）给出了一个清晰的刻画.

本节主要讨论素数幂次本原置换群的类型以及具体类型是否具有2重传递性.假设G是Ω上的本原置换群，且｜Ω｜＝pn，p是一个素数.则soc（G）＝T1×…×Tm≅Tm，T为单群.

下面的命题确定了素数幂次本原置换群G的本原类型.

命题1 设G是Ω上的本原置换群，且｜Ω｜＝pn，p是一个素数，则G是HA、AS或PA型.

证明 设G是Ω上的本原置换群，并且令H＝soc（G），则H＝T1× … ×Tm≅Tm.由O′Nan－Scott 定 理 知，G是 HA、AS、SD、TW、PA型.

假设G是SD型，则m≥2，｜Ω｜＝｜T｜m－1＝pn－1.于是T是p－群，就有T可解.而T是非交换单群，矛盾.假设G是TW型.则H是G的一个正则子群，故｜Ω｜＝｜Tm｜＝｜T｜m.由于T是非交换单群，这是不可能的.所以G只可能是HA、AS或者PA型.很明显HA中全是素数幂次本原群，而AS、PA中都含有素数幂次本原群.

假设G是AS型本原群，则G包含一个指数为pn的极大子群.而包含一个指数pn为的子群的非交换单群已经被Guralnick完全刻画［4］.

定理4 假设T是一个非交换单群且包含一个指数为素数幂pn的子群H.则下述之一成立：

（1）T≅Apn，且H≅Apn－1；

（2）T≅PSLd（q），H是T的一个极大抛物子群，且pn＝ （qd－1）／（q－1）；

（3）T≅PSL2（11），H≅A5，且p＝11；

（4）T≅M11，H≅M10，且p＝11；

（5）T≅M23，H≅M22，且p＝23；

（6）T≅PSU4（2），H≅Z42∶A5，且pn＝27.

我们知道所有2－传递群都是已知的，于是有下面的推论.

推论1 假设非交换单群T是集合Ω上的传递置换群，且｜Ω｜＝pn，p是一个素数，则要么T是2－传递，要么｜Ω｜＝27，T≅PSU4（2）本原但不是2－传递.

证明 设T是Ω上的传递置换群，令α∈Ω，则T∶Tα｜＝pn.由定理4，可以得到T和相应的Tα.通过对照文献［2］中2－传递群列表知，除了T≅PSU4（2），其余的T都是2－传递的.又由ATLAS知，Tα≅∶A5是T的指数为27的极大子群，所以T≅PSU4（2）在Ω上是本原的.

特别地，如果p＝2，则G＝A2n或PSL2（q），并且q＝2n－1是梅森素数.Burnside定理告诉我们，一个2－传递置换群是HA或AS型本原群.假设G是2－传递的，则soc（G）＝T是非交换单群，或者soc（G）＝为初等交换p－群.如果G是2－传递的，且soc（G）＝，α∈Ω，则G＝∶Gα≤AGLn（p），且Gα≤GLn（p）作用在向量空间V＝的非零向量上传递，这类群被Hering［10］以及Huppert［12］确定.

如果G是2－传递的，且soc（G）＝T是非交换单群，这类群被列在文献［2］中，通过检查核对，有如下定理.

定理5 假设G是Ω上的2－传递群，且soc（G）＝T是非交换单群，｜Ω｜＝pn（n≥2）.则G＝Apn，Spn或者PSLk（q）≤G≤PΓLk（q），其中（qk－1）／（q－1）＝pn.

下面假设G不是2－传递的，如果G是HA型本原群，则G＝∶Gα≤AGLn（p），且Gα≤GLn（p）是不可约的且作用在向量空间V＝的非零向量上不传递.这样的Gα的确定至今没有一般方法.于是便有下面的问题：

Open Problem：确定GLn（p）的所有不可约且作用在向量空间V＝的非零向量上不传递的子群.

如果G是PA型本原群，由O′Nan－Scott定理知，G是某个圈积U wr K的子群.于是PA型本原群只能出现在圈积中.关于乘积型本原群，有以下引理［3］：

引理6 假设H和K分别是Γ和Δ上的非平凡置换群，则圈积G＝K wr H通过乘积作用在Ω＝Δ｜Γ｜上是本原的当且仅当：

（1）Κ在Δ上本原但不正则；

（2）Γ有限并且H在Γ上传递.

特别地，若｜Ω｜＝pn，p为素数.有下面推论.推论2 圈积G＝K wr H通过乘积作用Ω上是本原的当且仅当下述之一成立.

（a）n为素数，K是引理5（2）中列出的群，并且Zn≤H≤Sn.

（b）n＝mk，K是pm次非正则本原群，且H≤Sk传递.

这一结果把素数幂次乘积型本原群的研究归约为对几乎单型数幂次本原群的研究.

4 本文主要定理的证明

在给出定理1的证明之前，先看｜Ω｜＝8的情形.

命题2 假设G是Ω上的本原置换群，其中｜Ω｜＝8，则G是下列群之一：

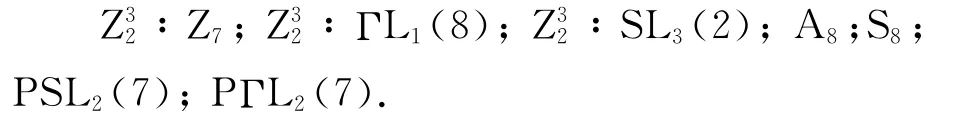
证明 通过文献［13］知，Ω上的本原而非2－传递群是不存在的，即G是Ω上的2－传递群.所以G是AS或HA型本原群.如果G是AS型，则soc（G）＝T是非交换单群.由定理5，则S≅A8，S8，PSL2（7）或者PΓL2（7）.如果G是HA型，令α∈Ω，则G＝∶Gα≤AGL3（2）.由Hering［10］的结果，有 Gα≤ ΓL1（8）或 者Gα＝ SL3（2），GL3（2）.而ΓL1（8）≅Z7∶Z3并且Z7是不可约的且循环传递作用在向量空间的非零向量上.又因SL3（2）≅GL3（2），所以 G＝∶Gα，其中 Gα≅Z7，ΓL1（8）或SL3（2）.

下面证明定理1.

定理1的证明 假设G是Ω上的本原置换群，且｜Ω｜＝pn，p是一个素数.令α∈Ω，H＝soc（G），则H＝T1×…×Tm≅Tm.

假设G是2－传递的.由Burnside定理，G是HA或AS型.如果G是HA型，则H＝，且G＝∶Gα≤AGLn（p），其中Gα≤GLn（p）作用在向量空间V＝的非零向量上传递，这类群被Hering［10］以及Huppert［12］确定.如果 G是AS型，则H＝T为非交换单群.由定理5，则G＝，G＝或者PSLk（q）≤ G≤PΓLk（q），其中（qk－1）／（q－1）＝pn.因此定理1（Ⅰ）成立.

现在假设G不是2－传递的.由命题1知，G是HA、AS或PA型.如果G是HA型，则G＝∶Gα≤AGLn（p），其中Gα≤GLn（p）不可约的且作用在向量空间V＝的非零向量上是不传递的.如果G是AS型，则H＝T为非交换单群.由推论1知，H≅PSU4（2）且｜Ω｜＝pn＝27.又有H ≤ G≤Aut（H）且Aut（H）＝PSU4（2）.2，所以 G≅PSU4（2）或者PSU4（2）.2.如果 G是PA型，则H＝soc（U）d◁G≤U wr K其中1＜d≤n，d｜n，且U是pr／d次AS或者SD型本原群.由命题1知，U是AS型，所以soc（U）＝T是非交换但群.由定理4知，T为Apn／d；PSLk（q），其中（qk－1）／（q－1）＝ pn／d；M11，其中 p ＝ 11，n ＝ d；PSL2（11），其中，p＝11，n＝d；M23，其中p＝23，n＝d；或者PSU4（2），其中1＜d＝n／3.又因圈积U wr K是PA型，由推论6知，K≤Sd传递.因此定理1（Ⅱ）成立.

［1］BURNSIDE W.On some properties of groups of odd order［J］.J.London Math.Soc.，1901，33：162－185.

［2］CAMERON P J.Finite permutation groups and finite simple groups［J］.Bull.London Math.Soc.，1981，13：1－22.

［3］DIXON J D，MORTIMER B.Permutation groups［M］.New York：Springer－Verlag，1996.

［4］GURALNICK R.Subgroups of prime power index in a simple group［J］.J.Algebra，1983，81：304－311.

［5］LIEBECK M W，SAXL J.The primitive permutation groups of odd degrees［J］.J.London Math.Soc，1985，31（2）：250－264.

［6］LI C H，SERESS Á.The primitive permutation groups of square－free degree［J］.Bull.London Math.Soc.，2003，35：635－644.

［7］LI C H.The primitive permutation groups of certain degrees［J］.Journal of Pure and Applied Algebra，1997，115：275－287.

［8］PRAEGER C E，LI C H，NIEMEYER A C.Finite transitive permutation groups and finite vertextransitive graphs［J］.Graph symmetry：algebraic methods and applications，NATO Adv.Sci.Inst.Ser.C，1977，497：277－318.

［9］DOBSON E，WITTE D.Transitive permutation groups of prime squared degree［J］.J.Algebra Combin，2002，16：43－69.

［10］HERING C.Transitive linear groups and linear groups which contain irreducible subgroups of prime order II［J］.J.Algebra，1985，93（1）：151－164.

［11］LIEBECK M W，PRAEGER C E，SAXL J.On the O′Nan－Scott theorem for finite primitive permutation groups［J］.J.Austral.Math.Soc.，1988，44（A）：389－396.

［12］HUPPERT B.Zweifach transitive，auflösbare Permutationsgruppen［J］.Math.Z，1957，68：126－150.

［13］JONES G A.The Sylowp－gruops of simply primitive group of degreep3［J］.Quart J.Math.Oxford，1977，28（2）：177－190.