W （0，1）型代数的二维中心扩张的导子代数＊

张嘉盛，高寿兰

（湖州师范学院 理学院，浙江 湖州313000）

0 引 言

文献［1］中引入了一类W（a，b）型李代数，它有一组基｛Lm，Jm，｜m∈Z｝，满足下列李运算：

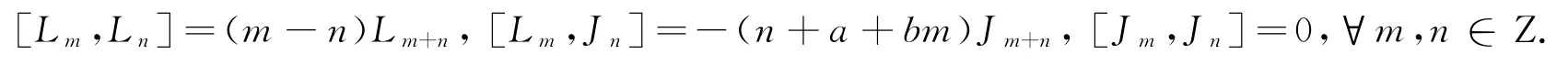
文献［1］对W（a，b）型李代数的结构进行了研究，确定了它们的2－上同调群.特别地，对于W（0，1）型李代数有：

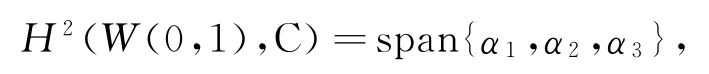
本文计算了带有α1、α3的W（0，1）的二维中心扩张P的导子代数，确定P有四个外导子.

本文用Z和C分别表示整数集和复数域，所有的向量空间都是复数域C上的线性空间.

1 预备知识

定义1.1［2］设M是一个交换群，g＝⊕m∈Mgm是M－阶化李代数.g－模V称为是M－阶化的，如果V＝Vn，gmVn⊆Vm＋n，∀m，n∈M.

定义1.2［2］设g是李代数，V是g－模.线性映射D：g→V称为一个导子，如果对任意的x，y∈g，有：

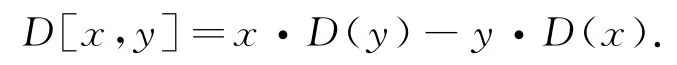
如果存在某个v∈V，使得D：x→x·v，那么称D为内导子.

设g是李代数，V是g－模.记所有的导子张成的空间和内导子张成的空间分别为Der（g，V）、Inn（g，V）.令H1（g，V）＝Der（g，V）／Inn（g，V）.为了方便，记g的导子代数和内导子代数分别为Der（g）、Inn（g）.

2 李代数P 的导子

定义2.1［1］李代数P是复数域C上的线性空间，有一组基｛Lm，Jm，C1，C2｜m∈Z｝，对任意的m，n∈Z满足下列李运算：

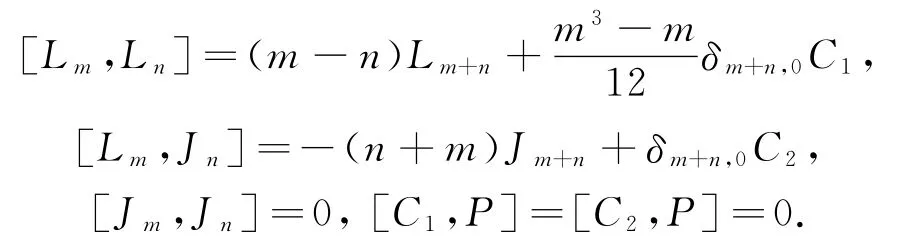
显然，P有2维中心span｛C1，C2｝.易知P是有限生成的，｛L－1，L－2，L1，L2，J1｝是P的一组生成元.P有一个自然的Z－阶化：P＝Pm，其中Pm＝span｛Lm，Jm，δm，0C1，δm，0C2｝，从而由文献［2］中命题1.1得下列引理：

引理2.1 Der（P）＝（Der（P））m，对任意的Dm∈（Der（P））m，Dm（Pn）⊆Pm＋n，∀m，n∈Z.

引理2.2H1（P0，Pm）＝0，∀m∈Z＼｛0｝.

证明 对于任意的μ∈H1（P0，Pm），设

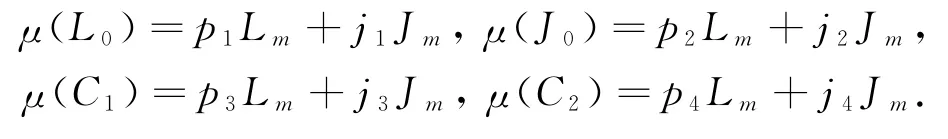
其中：pi，ji∈C；i＝1，2，3，4.

由μ［L0，C1］＝［μ（L0），C1］＋［L0，μ（C1）］，得：

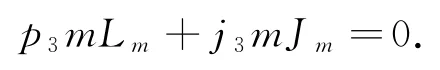
从而有p3＝0，j3＝0，即μ（C1）＝0.

由μ［P0，C2］＝［μ（P0），C2］＋［P0，μ（C2）］，得：

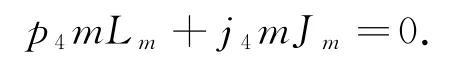
因此p4＝0，j4＝0，即μ（C2）＝0.

由μ［L0，J0］＝［μ（L0），J0］＋［L0，μ（J0）］，得：

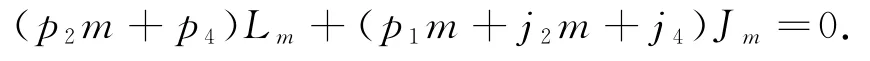
所以

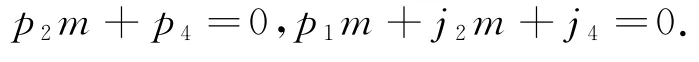
则p2＝0，p1＋j2＝0，即μ（J0）＝－p1Jm.由此可得：

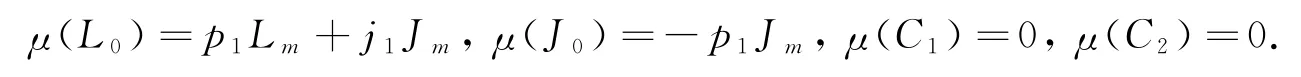
故μ∈Inn（P0，Pm）.由此可得：

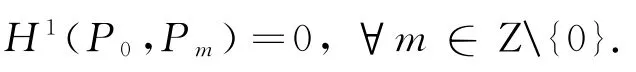
引理2.3 HomP0（Pm，Pn）＝0，∀m，n∈Z，且m≠n.

证明 设m≠n时，对任意的f∈HomP0（Pm，Pn），有：

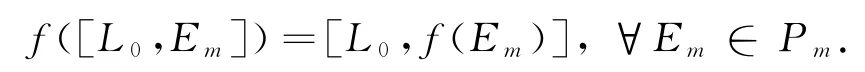
即

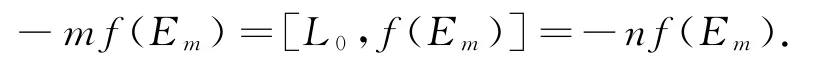
所以f（Em）＝0，从而可得f＝0.此引理成立.

根据引理2.2和引理2.3，以及文献［2］中命题1.2得下列引理：

引理2.4 Der（P）＝Der（P）0＋Inn（P）.

定理2.1H1（P，P）＝CD1⊕CD2⊕CD3⊕CD4，其中：D1（Jm）＝Jm；D1（C2）＝C2；D2（Jm）＝δm，0C1；D3（Jm）＝δm，0C2；D4（Lm）＝m2Jm＋δm，0C2；其余为零.

证明 对任意D∈（Der（P））0，设

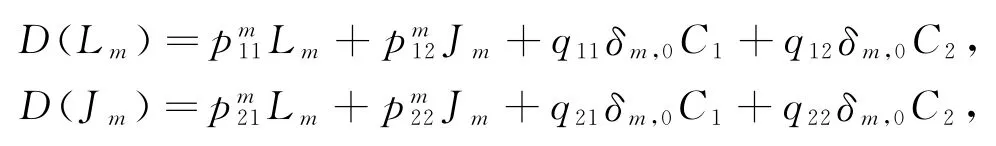
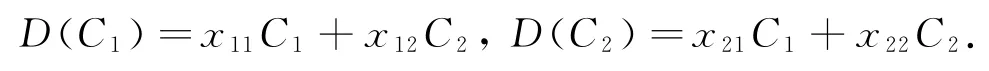
其中：，qij，xij∈C；i，j＝1，2.

由D［Lm，Ln］＝［D（Lm），Ln］＋［Lm，D（Ln）］，得：

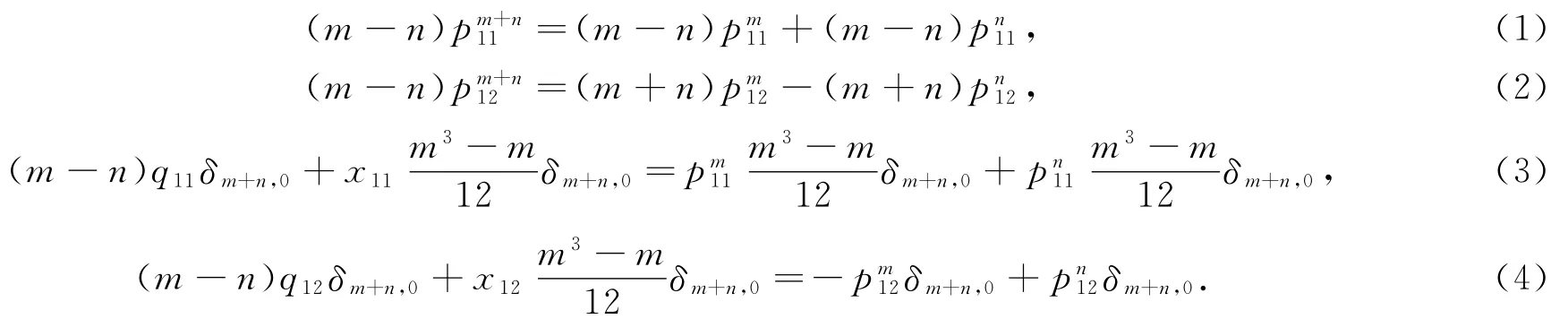
在（1）式中，令m＝0，n≠0，则有＝0，从而可得：

在（5）式中，令n＝－m，则有：

把n＝1代入（5）式中，得：

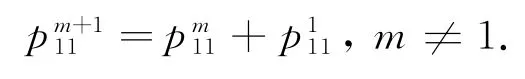
当m≥2时，由上式进行归纳可得：

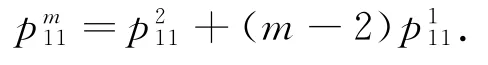
在（5）式中，令m＝－2，n＝1，并由（6）式得＝2，从而可得：

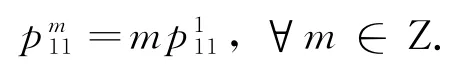
在（2）式中，当m＞0时，令n＝1，则有：

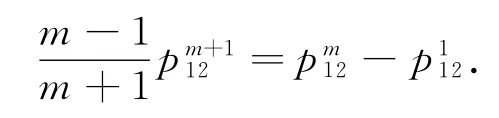
从而可得：

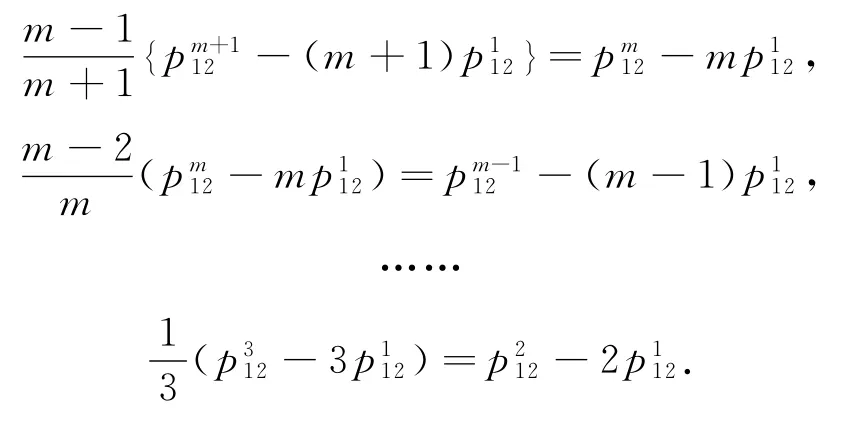
将上述等式等号两边相乘后，得：

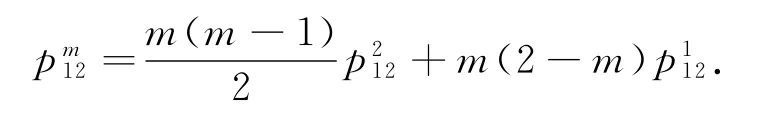
在（2）式中，令m＝2，n＝－1，则有3＝－，从而可得：

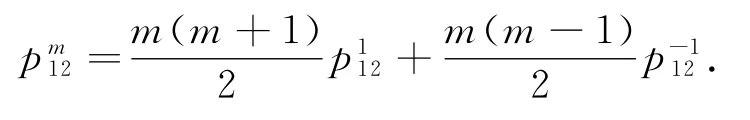
在（2）式中，当m＜0时，令n＝－1，则有：

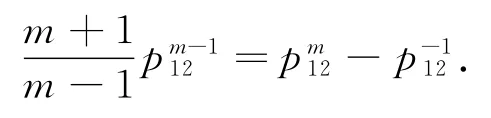
从而可得：

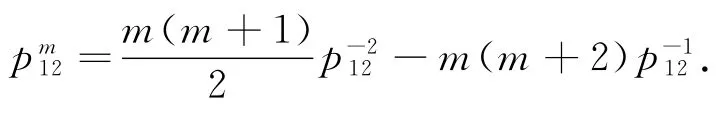
在（2）式中，令m＝－2，n＝1，则有＝3＋，从而可得：

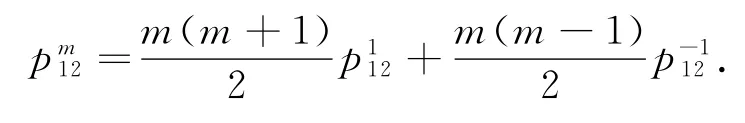
在（2）式中，令m＋n＝0，则有＝0，从而可得：

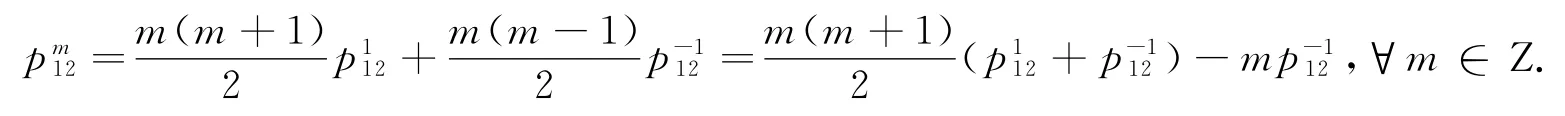
在（3）式中，令n＝－m，则有：

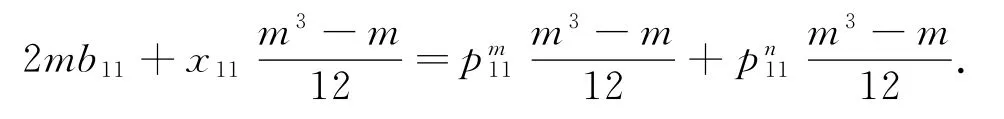
从而可得：

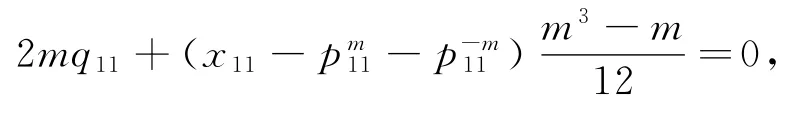
即

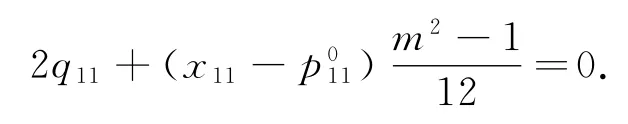
因为此式对任意m都成立，故q11＝0，x11＝0.

由（4）式可得对任意的m∈Z，有：

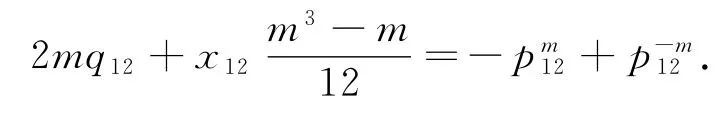
则

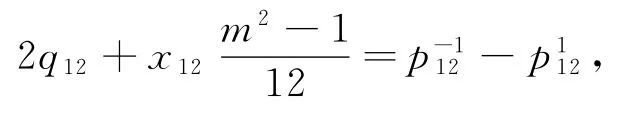
即

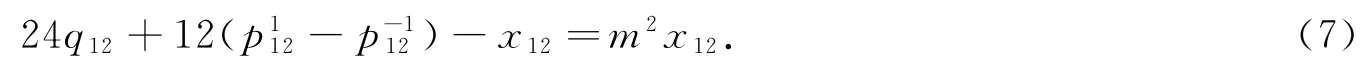
因为（7）式对任意m都成立，故x12＝0，.

由D［Lm，Jn］＝［D（Lm），Jn］＋［Lm，D（Jn）］，得：

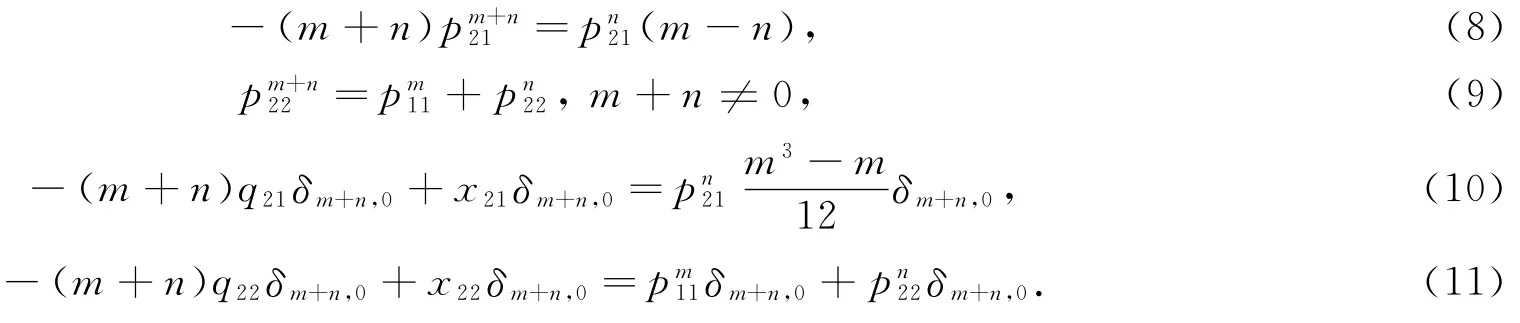
在（8）式中，当n≠0时，有＝0，再令m＝1，n＝0，即可得＝0，从而可得＝0，∀m∈Z.

在（9）式中，当m＋n≠0时，有：

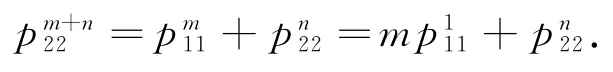
令n＝0，则有：

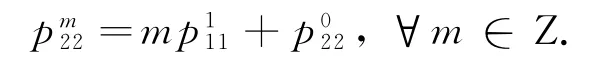
在（10）式中，令n＝－m，得：

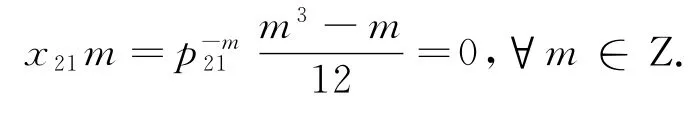
则有x21＝0.

由（11）式得：

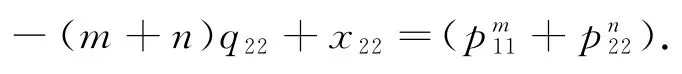
则

设a＝，2b＝＋，c＝，d＝，e＝q21，f＝q22，则有：

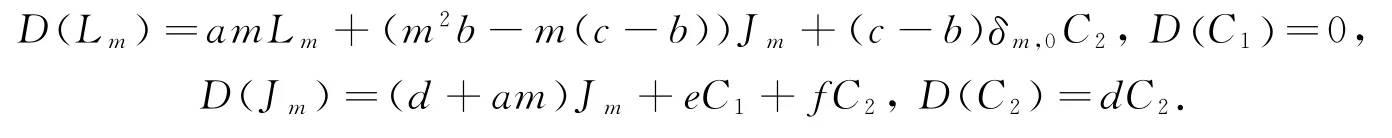
令D0＝ad（－aL0＋（c－b）J0），则有：

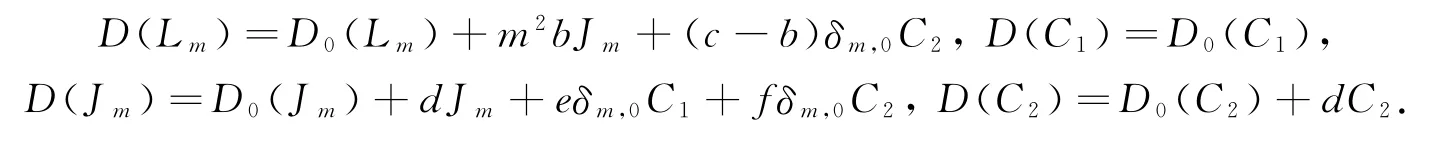
令＝D－D0，则有：

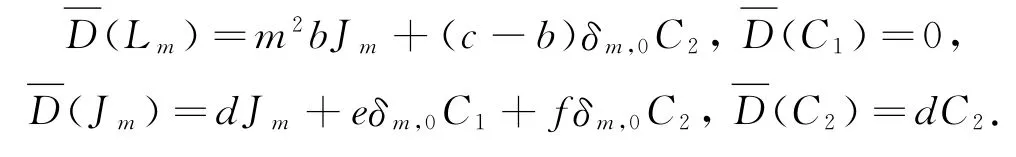
从而可得：

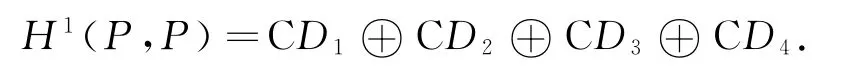
其中：D1（Jm）＝Jm；D1（C2）＝C2；D2（Jm）＝δm，0C1；D3（Jm）＝δm，0C2；D4（Lm）＝m2Jm＋δm，0C2；其余为零.这里D1，D2，D3，D4是P的4个线性无关的外导子.

定理证毕.

定理2.2 Der（P）＝Inn（P）⊕CD1⊕CD2⊕CD3⊕CD4，其中D1，D2，D3，D4如定理2.1所定义.

［1］Gao S，Jiang C，Pei Y.Low－dimensional cohomology groups of the Lie algebrasW（a，b）［J］.Comm Alg，2011，39（2）：397－423.

［2］Farnsteiner R.Derivations and extensions of finitely generated graded Lie algebras［J］.J Algebra，1988，118（1）：34－45.