高中数学教材“推广型”内容的教学策略

曾荣

数学推广是指在一定范围内或一定层次上对数学概念、定理、法则进行拓展，使之在更大范围或更高层次上成立，它是数学研究不可或缺的基本方法[1]。在高中数学教材中，设置了大量的“推广型”教学内容，如：将0°～360°角推广到任意角，将锐角三角函数推广到任意角的三角函数，将勾股定理推广到余弦定理，将平面几何中的向量方法推广到立体几何中的向量方法，等等。教师如能结合这些内容的教学，让学生经历推广的过程，体验数学在结构上的和谐性，并尝试通过类比、归纳、化归等思想方法解决在推广过程中遇到的困难和问题，必然对培养学生的创新思维具有重要意义。

一、“推广型”内容教学时需解决的问题

1.推广的必要性

解决推广的必要性问题，即要解决“为什么需要推广？”这一问题。教学中应从学生已有的认知水平出发，结合数学发展的现实基础和逻辑基础，让学生深刻领悟到进行推广的必要。例如，在引入大于360°的角和负角时，可以举些学生熟悉的生活中大于360°的角和负角，如体操中的转体、跳水中的翻腾、钟表中的指针、自行车的轮子、螺丝扳手与曲柄连杆等按不同方向旋转时所成的角，用以说明建立新概念的必要性和实际意义，这也有利于体验数学的人文价值，开阔学生的视野。

2.推广的方法性

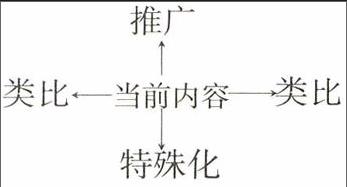
解决推广的方法性问题，即要解决“如何进行推广？”这一问题。从数学学习、研究过程来看，经常使用如下的逻辑思考方法：

其中突出显示了联系的观点，通过类比、推广、特殊化、化归等思想方法，可以极大地促进学生的数学思考，使他们更有效地寻找出自己感兴趣的问题，从中获得研究方法的启示。例如，关于平面几何中的向量方法，我们可以有如下的“联系图”：

3.推广的应用性

解决推广的应用性问题，即要解决“推广后有什么用？”这一问题。在联系旧知推广得到新知的基础上，要重视新知的应用，让推广的价值得到充分的展示。这种价值，不仅体现在新知对旧知的覆盖，更要让学生感受到一个数学概念的推广可能带来很多更好的性质。例如，将勾股定理推广到余弦定理以后，可以讲解这样的问题：用余弦定理证明：在△ABC中，当∠C为锐角时，a2+b2>c2;当∠C为钝角时，a2+b2

二、“推广型”内容的教学基本策略

1.创设具有认知冲突的问题情境，揭示推广的必要性

认知心理学家认为：当学习者发现不能用头脑中已有的知识来解释一个新问题，或发现新知识与头脑中已有的知识相悖时，就会产生“认知失衡”。这种认知冲突会让学生产生新奇和惊愕，从而引起学生的注意、关心和探究。认知冲突是教学和学习的最佳契机。在进行“推广型”教学内容的教学时，创设具有认知冲突的问题情境，将有利于推广必要性的揭示。

（1）情境生活化，使推广成为需要。解决现实生活和生产实际问题的需要，常常是进行数学推广最直接、最有力的推手。为此我们可以结合具体的实例创设情境，使新知自然生成。例如，我们将0°～360°角推广到任意角时，可创设如下问题情境。

案例1  角的概念的推广的问题情境

问题1 在初中我们是怎样定义角的？（从如下的静态和动态两个角度定义。）

问题2  平面内一条射线绕其端点旋转一周后回到原来的位置，所形成的角是什么角？如果继续旋转下去，所形成的图形还是不是角？为什么？

问题3  生活中存在刚才问题中所出现的角吗？你能试着举出一些实例吗？我们又如何去理解它们呢？

通过回顾旧知，联系生活实际，引发认知冲突，角的推广也就成了必然需求。

（2）关系普遍化，使推广成为必要。推广常用的方式是将变量之间、对象之间的特殊关系改为一般关系而获得具有普遍意义的命题及公式，或是将具体对象改为一般对象从而使命题得到推广[2]。教学时，一般先复习包容性小、抽象概括程度低的概念，并在此基础上创设具有认知冲突的问题情境。例如，将锐角三角函数推广到任意角的三角函数的学习，从认知结构发展的角度来说，是属于“下、上位关系学习”，“先行组织者”是锐角三角函数的概念[3]。教学时，可创设如下问题情境。

案例2  任意角的三角函数的问题情境

问题1  你能回忆一下锐角三角函数的定义吗？

问题2  你能用直角坐标系中角的终边上的点的坐标来表示锐角三角函数吗？如果按这种方式用坐标表示的三角函数值，在锐角取值范围内和之前的定义吻合吗？

问题3  改变终边上的点的位置，这三个比值会改变吗？为什么？（在定义任意角的三角函数之前，必须让学生感知、确认、理解这三个比值都只与角的大小有关，而与点在终边上的位置无关，因此它们都是以角为自变量的函数，从而给出任意角的三角函数的定义。）

问题4  角的范围已经推广到了任意角，那么，仿照以上锐角三角函数的新的定义方式，你认为如何定义任意角三角函数比较合理？

通过以上问题串，由特殊到一般，思维流畅，层层深入，新概念的得出水到渠成。

2.迁移已有的思想方法，凸显推广的方法性

新课标强调“四基”，即学生通过学习，获得必需的基本知识、基本技能、基本思想方法、基本活动经验。基本思想方法、活动经验的获得，不仅来源于自己平时对知识的感悟，更多的来源于平时教师对思想方法的提炼、渗透。学会推广实际上就是学会方法。教师在进行“推广型”教学内容的教学时，应注意迁移已有的思想方法，如类比探究、化归论证等，让学生在推广的过程中感悟方法、掌握方法。

（1）类比探究。类比法通过比较两个对象的部分相同或相似，推出其他方面也可能相同或相似。类比是进行数学再发现的有效方式。在进行角的概念推广的教学时，为了引出正角、负角和零角的概念，我们可设置如下类比式问题串。

案例3  类比正数、负数、零的概念，得出正角、负角、零角的概念

问题1  如何用数学的方法将按顺指针、逆时针两种不同的方向旋转的角加以区分？你以前有过类似的经验吗？

问题2  我们知道，正负数和0可借助数轴有效地进行区分。那么，为了区分按顺指针、逆时针两种不同的方向旋转的角，你认为可以利用什么载体进行区分呢？如何给它们下一个合理的定义呢？

通过以上问题，利用类比的方法，由正数、负数、零的概念自然引出正角、负角、零角的概念，同时也让学生体验从低维问题向高维问题发展的一般方法。

（2）化归论证。一般化是数学推广的基本方式。数学家G·波利亚指出：”一般化是从对象的一个给定集合进而考虑到包含这个集合的更大集合。”由下位公式向上位公式推广时常伴随着猜想，而要对这种猜想进行论证，则常需将上位公式化归至下位公式。例如，我们在将勾股定理推广到余弦定理时，可按如下方式进行。

案例4  借助化归的思想论证余弦定理

问题1  前面学过的正弦定理的表达式是怎样的？它具有怎样的功能？

问题2  在我们所学知识中，有没有涉及已知三角形的两边及夹角，求第三边的情形呢？能否举一个具体的例子？

问题3在△ABC中，已知边a，b，∠C≠90°，是否还能用勾股定理求边c？（很自然的想法是构造直角三角形，以便用勾股定理进行计算。辅助线如下图，过程略。）

3.运用推广的结论方法，强化推广的应用性

旧知推广为新知以后，内涵发生了改变，伴随产生了一些新的性质。为了让学生巩固新知，体验数学的实用价值，我们应在推广之后，在概念的辨析、性质的应用等方面及时加以应用。

（1）概念辨析，厘清疑点。数学概念在得到推广以后，其内涵发生了改变，容易与原有的概念产生混淆。为了帮助学生区分新旧概念的区别，加深理解，我们可以通过概念辨析题的方式进行新知的应用。如，将角推广到任意角以后，伴随着产生了象限角、轴线角等概念。这些概念与原有的锐角等概念容易混淆，为此我们可通过如下判断题进行辨析。

案例5  角的概念推广后设置的概念辨析题

判断下列说法是否正确：

①锐角是第一象限角。（对）

②第一象限的角都是锐角。（错）

③小于90°的角都是锐角。（错）

④第二象限的角一定比第一象限的角大。（错）

⑤终边相同的角一定相等。（错）

⑥终边相同的角有无数多个，它们相差360°的整数倍。（对）

（2）前后呼应，变式应用。在问题情境的创设过程中，常借助认知冲突，设置悬念，引发推广。在推广以后，要及时解决原先的疑问，并适当深入，变式提升。例如，前面为了将勾股定理推广到余弦定理，设计了这样的问题：已知三角形的两边及夹角，如何求第三边呢？那么，我们可结合此问题的解决，设计例题及变式。

案例6  将勾股定理推广到余弦定理后设置的例题及变式

①在△ABC中，已知边b=3，c=1，∠A=60°，求边a。

②在△ABC中，已知边a=4，b=5，c=6，求∠A。

变式1在△ABC中，已知边a=4，b=5，c=6，判定在△ABC的形状。

变式2在△ABC中，已知边a∶b∶c=3∶4∶5，判定在△ABC的形状。

知识、能力与学习品质的提升是学生发展的基本目标。通过“推广型”教学内容的教学，让学生充分认识推广的必要性、方法行、应用性，在推广中进行再发现，学会探究，对学生良好数学素养的提升具有较大的帮助。

参考文献

[1] 徐彦辉.数学推广及其常见形式举例分析[J].数学通报，2010（4）.

[2] 孙世华.数学推广的基本模式[J].数学通讯，2005（1）.

[3] 陶维林.任意角的三角函数的设计与反思[J].中国数学教育，2009（4）.【责任编辑  郭振玲】