基于PH 曲线插值的圆锥曲线逼近
郑志浩,汪国昭
(浙江大学 数学科学学院,浙江 杭州310027)
将式(9)及ω(t)的表达式代入式(10)和(11),整理后得到以下方程组:
在计算机辅助几何设计中,圆锥曲线可用带权因子的有理多项式表示,权因子的易控特点使得圆锥曲线具有很强的几何灵活度,因而被广泛用于航空和汽车工业设计、机械加工、路径规划及艺术字体的造型中.利用圆锥曲线进行几何造型会频繁涉及放样与拼接问题,其中蕴含了大量的曲线求交工作,因此,须进行有理多项式与多项式的系统转化,其主要方法就是用多项式对圆锥曲线进行高精度逼近[1-6].同时,几何造型会频繁处理等距线的构造及弧长计算问题.由于目前圆锥曲线(除圆弧外)的弧长或等距线往往不能用多项式或有理多项式表示,不兼容于现有的NURBS系统,因此,对圆锥曲线进行弧长表示的有理转化是一种非常有效的方法.PH曲线是Farouki[7]引入的一种新颖的多项式曲线,即平面多项式参数曲线P(t)=(x(t),y(t))是PH 曲线的充要条件如下:存在多项式σ(t)使得关系式x′2(t)+y′2(t)=σ2(t)成立.PH 曲线主要特征是其弧长和等距线可用多项式及有理多项式表示.自引入PH 曲线后,许多学者对其进行了广泛研究,并用来对曲线作插值逼近.主要成果包括:由曲线端点条件插值生成G1的三次PH 曲线或PH 样条[8-10];Pelosi等[11]利用解非线性复方程的方法构造C2五次PH 样 条 曲 线;Moon 等[12]用 复 分 析 中 的Minkowski几何代数法研究了五次PH 插值曲线的形状与端点插值条件的关系;Sir等[13]由端点C1的Hermite插值条构造五次PH 样条曲线,逼近误差阶数为4;Juettler[14]由基曲线端点,基曲线端点一阶导数及端点曲率为插值条件,插值方程通过适当的坐标变换得到相关代数参量的四次方程,生成G2连续的七次PH 逼近曲线;Sir等[15]构造了次数更高的九次PH 样条曲线,逼近误差阶数为6;Wang等[16]对四次PH 曲线的控制多边形的几何结构作了深入研究,给出了四次Bézier曲线成为PH 曲线的边角分离的几何条件.张伟红等[17]利用五次PH曲线对圆弧作了等弧逼近.方林聪等[18]在C1Hermite插值条件下构造了2类六次PH 曲线,并能自由选择奇异点的位置.杨平等[19-20]讨论了七次Bézier曲线为PH 曲线的几何条件.此外,PH 曲线还应用于过渡曲线的构造和逆向工程[21-25].
在现有PH 插值及逼近结果基础上,本文进一步探讨较为新颖的四次PH 曲线及一类特殊的五次PH 曲线(具有保弧长的特点)的插值生成算法.分别从几何结构及复分析的角度具体构造G1插值的PH 曲线来对圆锥曲线作逼近.由于大量涉及圆锥曲线逼近的研究所采用误差度量均是Hausdorff距离[1-6],本文同样给出这些逼近的Hausdorff距离误差估计.
1 圆锥曲线及其逼近误差定义
平面内的圆锥曲线b(t)=(bx(t),by(t))可用二次有理Bézier曲线表示为

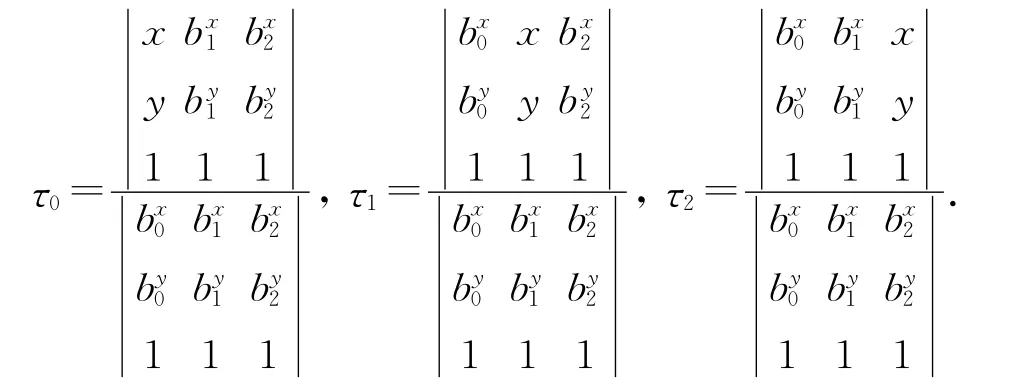
则X=τ0b0+τ1b1+τ2b2,τ0+τ1+τ2=1.
定义1 同一参数区间[0,1.0]内的2条平面曲线p(t)及q(t)的Hausdorff距离定义为
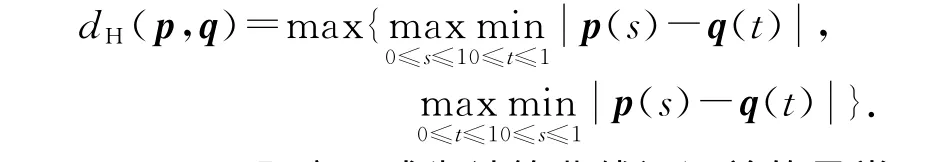
Hausdorff距离已成为计算曲线间误差的最常用的测度方式.特别针对圆锥曲线的逼近,Floater[4]还给出以下结论.
定理1 包含于Δb0b1b2的连续曲线r(t),t∈[0,1],满足r(0)=b0,r(1)=b2,{τj}2j=0是r(t)关于Δb0b1b2的三重心坐标,则r(t)与圆锥曲线b(t)的Hausdorff误差距离上界有如下估计式:
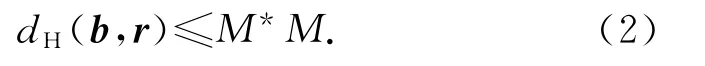
式中:

2 用四次PH 逼近圆锥曲线
对式(1)所表示的圆锥曲线,本章将根据其端点及端点单位切向量来构造G1四次PH 插值曲线,把该PH 曲线作为圆锥曲线的插值逼近曲线,并利用定理1进行误差估计.
2.1 G1 四次PH 曲线的插值构造
在复平面中,四次Bézier曲线的参数多项式P(t)=(x(t),y(t))可 表 示 成 复 数 形 式P(t)=x(t)+i y(t),P(t)是四次PH 曲线的充分必要条件是:存在一次实多项式w(t)=α(1-t)+t及一次复多项式G(t)=β(1-t)+γt(α为实系数,β与γ 为复系数),使得P′(t)=w(t)G2(t).基于复分析的方法,Wang等[16]给出四次PH 曲线的控制多边形几何特征,如定理2所述.
定理2 四次Bézier曲线
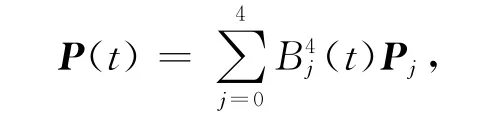

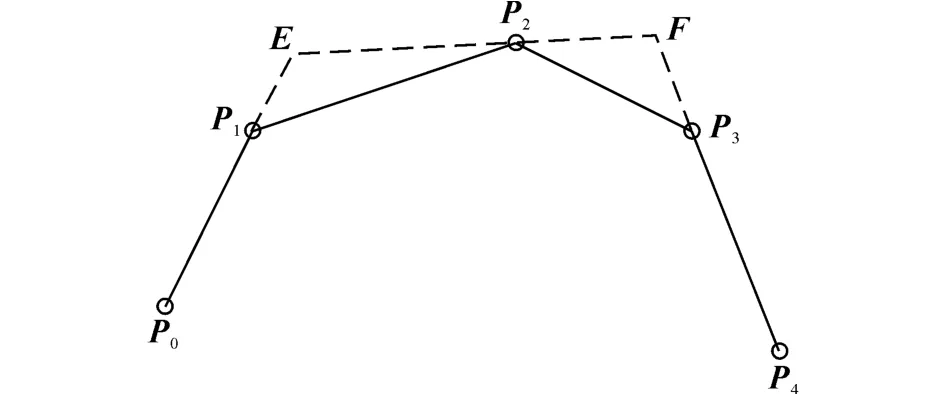
图1 四次Bézier曲线的控制多边形Fig.1 Control polygon of quartic Bézier curve

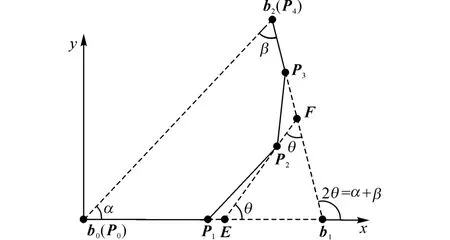
图2 圆锥曲线及四次PH 曲线的控制多边形Fig.2 Conic section and control polygon of PH quartic
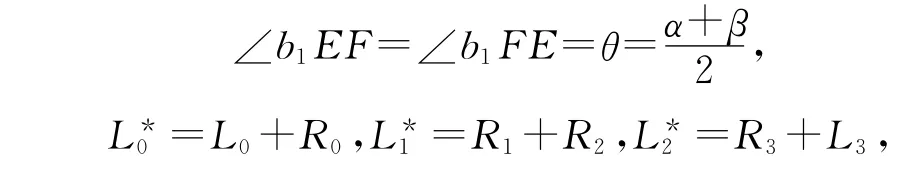
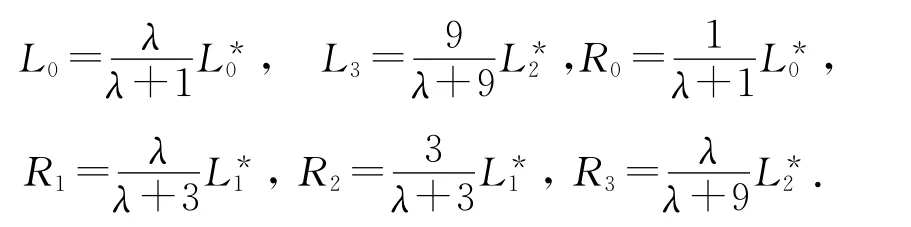

式中:
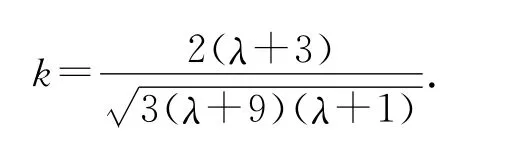
因此,P(t)的控制顶点可用上述有关边长及角度几何量表示:
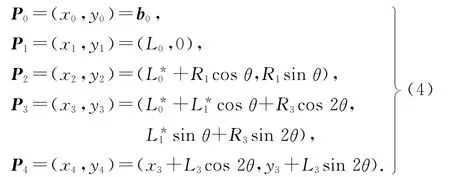
式中:λ可自由选取.当λ为某一特定值时,只要求出L*0、L*1、L*2就能同时算出L0、L3、R1、R3,由式(4)产生四次PH 曲线的控制顶点坐标.为此,利用插值条件P4=b2,对应以下方程组:
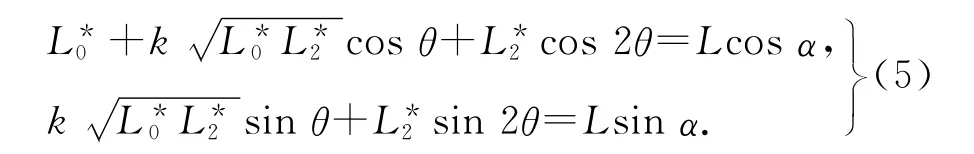
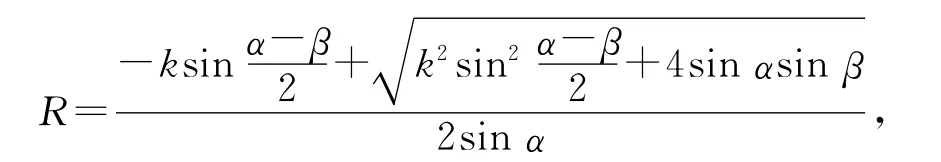

因此,在设定λ值后,能直接解出L*0、L*1、L*2,得到PH 曲线的控制顶点.
由上述边长L*0、L*1、L*2的关系可知,k=1 即λ=3,就有

若取P*0=b0、P*1=E、P*2=F、P*3=b2,所构造的三次Bézier曲线

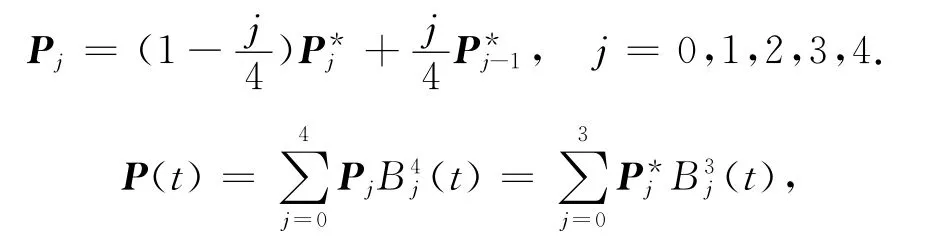
四次PH 曲线可退化成三次PH 曲线.
2.2 插值逼近的误差
当以圆锥曲线的端点及端点单位切向为插值条件构造了四次PH 逼近曲线后,进一步来估计逼近误差.不妨设

则四次PH 曲线的控制顶点{Pj与点b0、b1、b2就有以下线性组合关系:
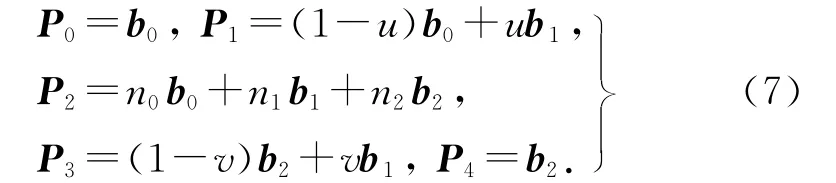
式中:n0、n1、n2是 点P2关 于Δb0b1b2的 重 心 坐 标,通过具体计算得到
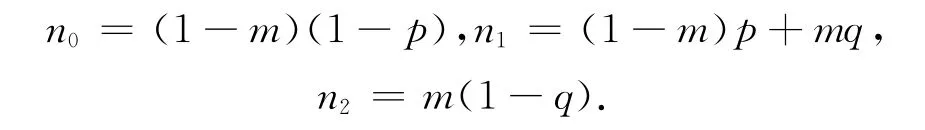
将式(7)代入
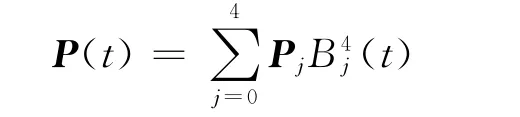
整理后化成τ0b0+τ1b1+τ2b2的线性组合形式,系数{τj就是P(t)关于Δb0b1b2的重心坐标,计算结果如下:

进一步计算可得
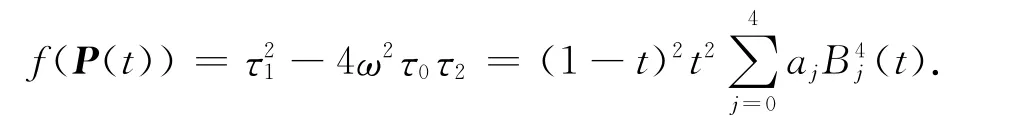
这里Bernstein基函数的系数分别为
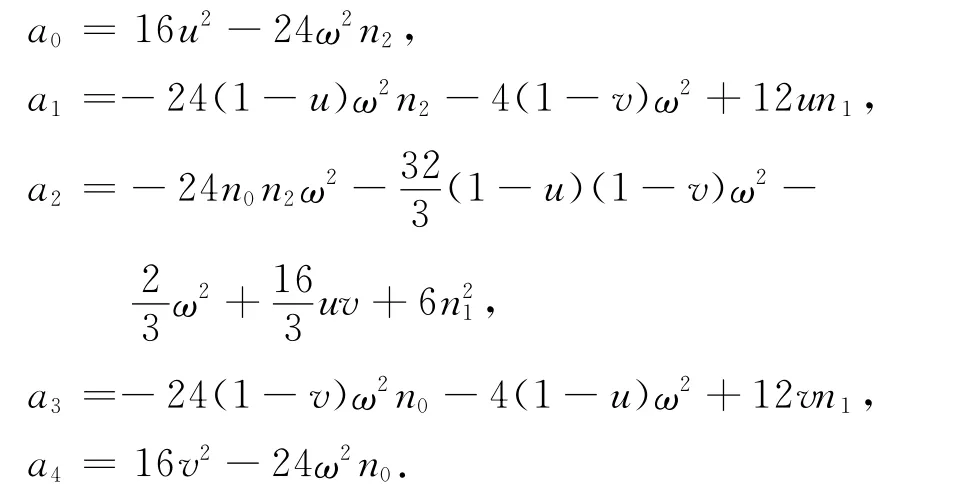
总结以上的分析及结论,得到如下误差定理和推论.
定理3 圆锥曲线b(t)与由其端点G1Hermite插值产生的四次PH 曲线P(t)的Hausdorff距离误差有以下估计:
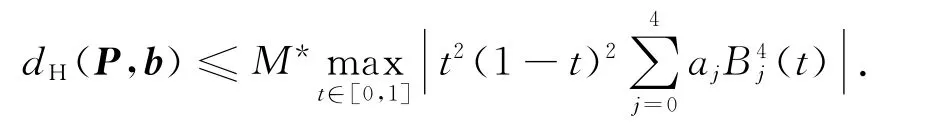
对于以上估计式,为获得最大值,可能会涉及解六次多项式方程,但精度较高.如为了避免解方程,由定理3的结论进一步可得以下推论.
特别地,当λ=3时,插值构造的四次PH 曲线退化为由式(6)所表示的三次PH 曲线.误差计算可通过次数较低的三次PH 曲线P*(t)计算.设

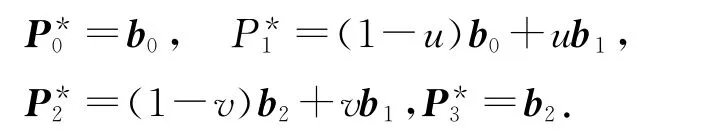
那么,P*(t)关于Δb0b1b2的重心坐标为τ0=3(1-u)(1-t)2t+(1-t)3,τ1=3u(1-t)2t+3v(1-t)t2,τ2=t3+3(1-v)(1-t)t2.
考虑函数
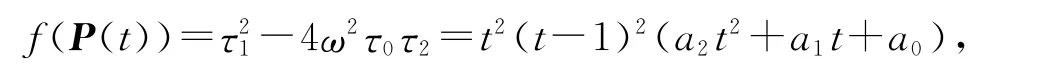
式中:
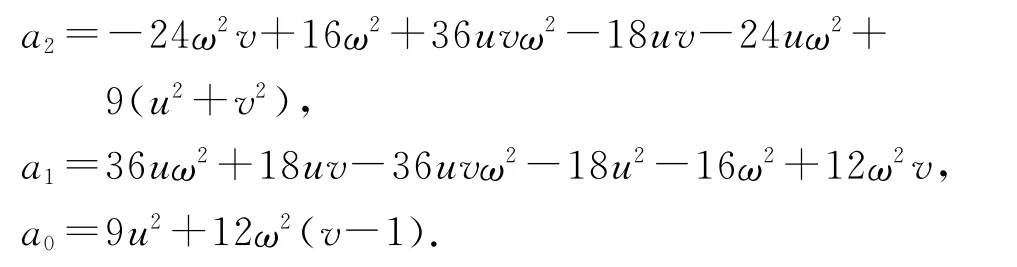
总结以上过程又有以下推论.
推论2 当λ=3时,四次PH 曲线P(t)对b(t)的逼近退化为三次PH 曲线(6)对b(t)逼近.
两者间的Hausdorff距离误差估计如下:
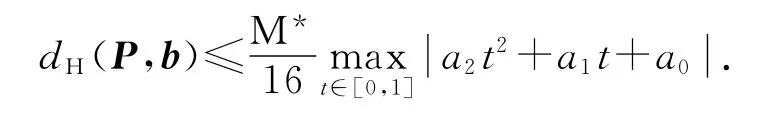
3 用五次PH 曲线逼近圆锥曲线
复数形式的五次Bézier曲线为
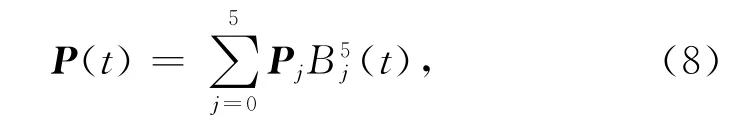
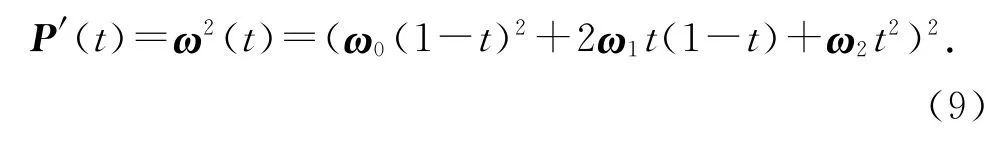
若点P0确定,则其余控制顶点为
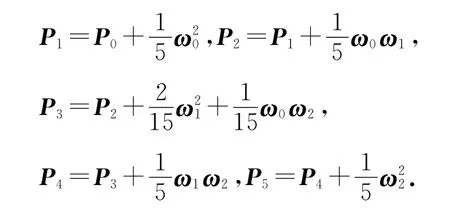
3.1 逼近的误差估计
在△b0b1b2内构造插值圆锥曲线端点及其单位切向的G1五次PH 曲线.根据要求可知,点P1、P4应 分 别 在b0-b1和b1-b2的 边 上,点P2、P3为△b0b1b2的内点,因此,PH 曲线的控制顶点与点b0、b1、b2存在以下线性关系:

式中:
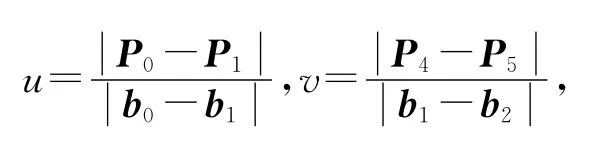

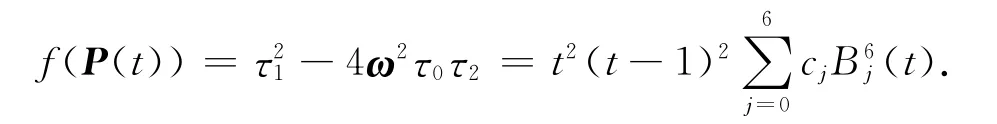

总结以上结果得到定理4.
定理4 圆锥曲线b(t)与插值逼近的五次PH
曲线P(t)的Hausdorff距离估计式为

定理4的最大值可通过八次多项式方程求解得到,精度较高.同样分析定理4 的结论进一步得到推论3.

3.2 插值曲线的类型
要构造对圆锥曲线插值逼近的G1五次PH 曲线,即只要确定复系数{ωj}2j=0,用定理4或推论3可估计逼近误差.关于复系数的确定可采用以下2种方式.
1)基于C1插值逼近.
为使插值产生的五次PH 曲线在圆锥曲线点达到C1,参照Moon[12]的结论,取系数
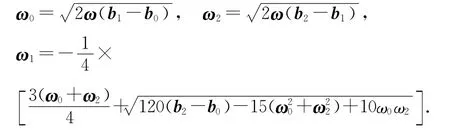
2)G1等弧方式逼近圆锥曲线.
为了得到更高的逼近精度,主要采用等弧逼近的方式.如果逼近曲线与基曲线保持弧长的一致性,那么曲线的内在几何特征就能充分得以体现.比如:当在路径规划设计中使用逼近算法时,基曲线与逼近曲线弧长的对应就很重要,逼近曲线应保弧长.
在此要解决的问题是:由式(1)所表示的圆锥曲线的弧长为S,现根据其端点及其端点的单位切向量(一阶几何Hermite插值条件),构造与之等弧长的五次PH 逼近曲线P(t).参照图2 的坐标系,以点b0为原点且b0的切向为x 轴正向,末端点b2的切向与x 轴的夹角为2θ.由于P(t)插值端点b0、b2及其单位切向T0、T1,故
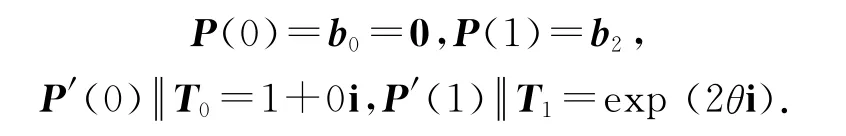
从而ω0为实数,记为ω0,为减少计算参数,设定五次PH 曲线的两端点切向量模长相等,即取ω2=ω0exp(iθ),另外ω1=ω1x+iω1y.由P(t)插值两端点b0、b2得到
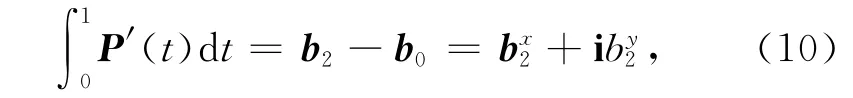
及PH 曲线的弧长同为S,则
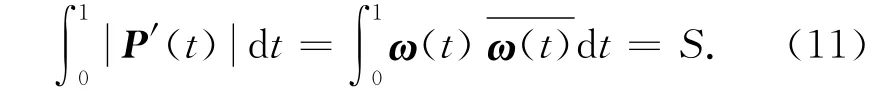
将式(9)及ω(t)的表达式代入式(10)和(11),整理后得到以下方程组:

由式(12)、(14)得到
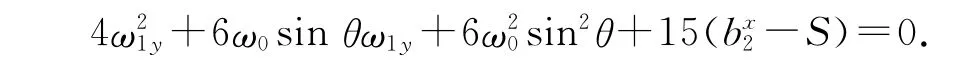
取

由式(13)解得
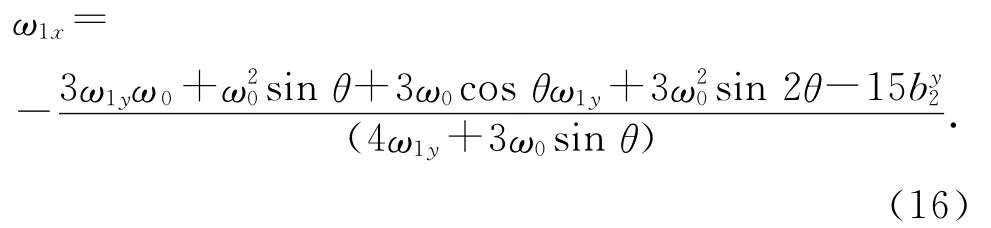
再将ω1x、ω1y的表达式代入式(14),经整理后产生了关于ω0的四次多项式方程:


解方程式(17),特别取


4 实 例
为了更好地说明本文中各类PH 插值曲线对圆锥曲线的逼近应用,列举如下2个实例.


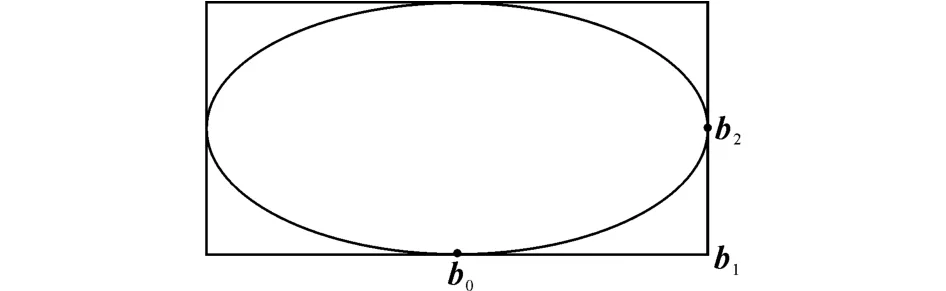
图3 椭圆及1/4段的控制顶点Fig.3 Ellipse and control polygon of quarter section

图4 例1的误差主项函数Fig.4 Key function for error in example 1

表1 用PH曲线逼近1/4椭圆段的Hausdorff距离误差估计Tab.1 Hausdorff distance evaluation between quarter section of ellipse and PH quartics

图5 离散后的两等弧逼近曲线及控制多边形Fig.5 Two approximation curves preserving arc-lengths and their control polygons after subdivision
若要获得更高的逼近精度,可将表示椭圆段的二次有理Bézier曲线在肩点(t=1/2)处离散成2段子曲线b1(t)与b2(t)(见图5):
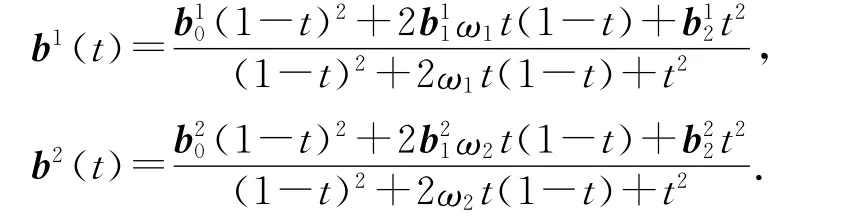
b1(t)与b2(t)对应的控制顶点及权因子为

如果对这两离散段分别构造五次PH 曲线作等弧逼近,则第一段误差估计值为σ=0.127 9×10-3,而第二段误差估计值为σ=0.001 2.由此可见,适当地对圆锥曲线进行离散可以使逼近精度迅速提高.当离散段数较多时,误差估计式采用推论1及推论3可避免多次解方程.

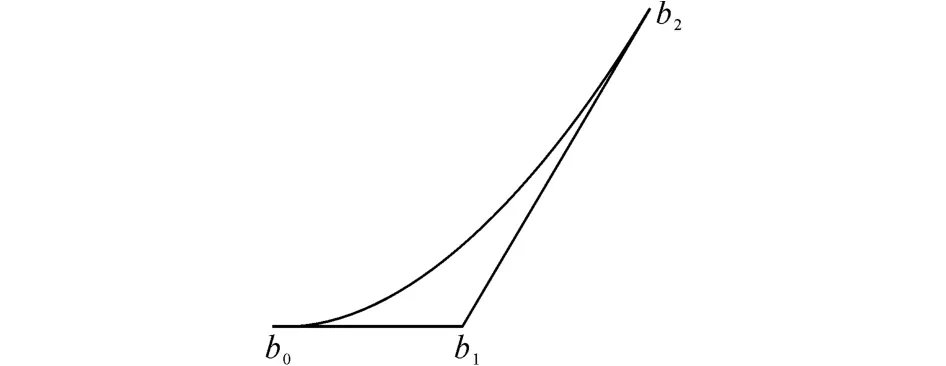
图6 抛物线及控制顶点Fig.6 Parabola and control polygon
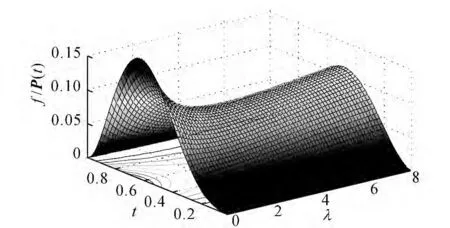
图7 例2的误差主项函数Fig.7 Key function for error in example 2

表2 例2的误差主项函数Hausdorff距离误差估计Tab.2 Hausdorff distance evaluation between parabola and PH quartics in example 2
5 结 语
采用四次PH 曲线及具有保弧长特征的五次PH 曲线可对圆锥曲线进行插值逼近.基于对控制多边形边角分离的几何结构分析,得到四次PH 曲线退化为三次PH 曲线的条件.利用不同类型的PH 曲线逼近圆锥曲线的Hausdorff距离误差的估计结果,可选取适当类型的PH 曲线,在用户给定的误差范围内,将圆锥曲线转化成PH 曲线.若要提高转化精度,可利用二次有理Bézier曲线的中点离散公式将圆锥曲线离散成多段曲线,再分别对各离散段构造插值逼近的PH 曲线,而对应的PH 曲线段将组成C1、G1的样条曲线.采用PH 曲线转化的方法,不仅实现了圆锥曲线的多项式的表示,还能得到弧长的多项式表示形式及等距线的有理形式,对减少计算量、压缩数据量都有一定的贡献.为获得更高连续阶的逼近曲线,在今后工作中将研究用六次及七次PH 曲线构造G2插值逼近曲线,并继续将本文的逼近思想应用到对其他类型曲线的逼近.
(
):
[1]AHN Y J.Approximation of conic section by curvature continuous quartic Bézier curves[J].Computers and Mathematics with Applications,2010,60(7):1986-1993.
[2]FANG L.G3approximation of conic sections by quintic polynomial curves[J].Computer Aided Geometric Design,1999,16(8):755-766.
[3]FLOATER M.High-order approximation of conic sections by quadratic splines[J].Computer Aided Geometric Design,1995,12(6):617-637.
[4]FLOATER M.An O(h2n)Hermite approximation for conic sections[J].Computer Aided Geometric Design,1997,14(2):135-151.
[5]KIM S H,AHN Y J.An approximation of circle arcs by quartic Bézier curves[J].Computer-Aided Design,2007,39(6):490-493.
[6]AHN Y J.Helix approximations with conic and quadratic Bézier curves[J].Computer Aided Geometric Design,2005,22(6):551-565.
[7]FAROUKI R T.The conformal map z→z2of the hodograph plane [J].Computer Aided Geometric Design,1994,11(4):363-390.
[8]LI Y J,DENG C Y.2012.C-shaped C2Hermite interpolation with circular precision based on cubic PH curve interpolation [J].Computer-Aided Design,2012:44(11),1056-1061.
[9]MEEK D S,WALTON D J.Geometric Hermite interpolation with Tschirnhausen cubics[J].Journal of Computational and Applied Mathematics,1997,81(2):299-309.
[10]BYRTUS M,BASTL B.G1Hermite interpolation by PH cubics revisited[J].Computer Aided Geometric Design,2010,27(8):622-630.
[11]PELOSI F,SAMPOLI M L,FAROUKI R T,et al.A control polygon scheme for design of planar C2PH quintic spline curves[J].Computer Aided Geometric Design,2007,24(1):28-52.
[12]MOON H P,FAROUKI R T.Construction and shape analysis of PH quintic Hermite interpolants[J].Computer Aided Geometric Design,2001,18(2):93-115.
[13]SIR Z,FEICHTINGER.F,JUETTLER B.Approximating curves and their offsets using baircs and Pythagorean hodograph quintic[J].Computer-Aided Design,2006,38(6):608-618.
[14]JUETTLER B.Hermite interpolation by Pythagorean hodograph curves of degree seven[J].Mathematics of Computation,2000,70(235):1089-1111.
[15]SIR Z,JUETTLER B.Constructing acceleration continuous tool paths using Pythagorean Hodograph curves[J].Mechanism and Machine Theory,2005,40(11):1258-1272.
[16]WANG G Z,FANG L C.On control polygon of quartic Pythagorean-hodograph curves[J].Computer Aided Geometric Design,2009,26(9):1006-1015.
[17]张伟红,蔡亦青,冯玉瑜.圆弧的五次PH 曲线等弧长逼近[J].计算机辅助设计与图形学报,2010,22(7):1082-1086.ZHANG Wei-hong,CAI Yi-Qin,FENG Yu-yu.Arclength-preserving approximation of circular arcs by quintic PH quintic PH curves[J].Journal of Computer-Aided Design and Computer Graphics,2010,22(7):1082-1086.
[18]方林聪,汪国昭.六次PH 曲线C1Hermite插值[J].中国科学:数学,2014,44(7):799-804.Fang Lin-cong,Wang Guo-zhao.C1Hermite interpolation using sextic PH curves[J].SCIENCE CHINA Mathematics,2014,44(7):799-804.
[19]杨平,汪国昭.7次PH 曲线的控制多边形的几何性质[J].计算机辅助设计与图形学报,2014,26(3):378-384.YANG Ping,WANG Guo-zhao.Geometric properties of control polygon of septic PH curve[J].Journal of Computer-Aided Design and Computer Graphics,2014,26(3):378-384.
[20]杨平,汪国昭.C3连续的七次PH 样条闭曲线插值[J].浙江大学学报:工学版,2014,48(5):934-941.YANG Ping,WANG Guo-zhao.C3Spline interpolation by Pythagorean hodograph closed curve of degree seven[J].Journal of Zhejiang University:Engineering Science,2014,48(5):934-941.
[21]郑志浩,汪国昭.三次PH 曲线的曲率单调性及过渡曲线构造[J].计算机辅助设计与图形学报,2014,26(8):1219-1224.ZHENG Zhi-hao,WANG Guo-zhao.On curvature monotony for a PH cubic curve and constructing transition curve[J].Journal of Computer-Aided Design and Computer Graphics,2014,26(8):1219-1224.
[22]WALTON D J,MEEK D S.G2curve design with a pair of Pythagorean hodograph quintic spiral segments[J].Computer Aided Geometric Design,2007,24(5):267-285.
[23]HABIB Z,SAKAI M.On PH quintic spirals joining two circles with one circle inside the other[J].Computer-Aided Design,2007,39(2):125-132.
[24]FAROUKI R T,GIANNELLI C,SESTINI A.Identification and“reverse engineering”of Pythagorean-hodograph curves[J].Computer Aided Geometric Design,2015,34(1):21-36.
[25]FAROUKI R T,SIR Z.Rational Pythagorean-hodograph space curves[J].Computer Aided Geometric Design,2011,28(2):75-88.

