正多面体对称群生成元的计算方法
欧阳培昌,占小根,邓志云,范发明
正多面体对称群生成元的计算方法
*欧阳培昌,占小根,邓志云,范发明
(井冈山大学数理学院,江西,吉安 343009)
借助三维正多面体的几何意义,可以直接推导其矩阵生成元,但因在三维空间无法建立真实的正多胞体(regular polytopes,正多面体在更高维空间的推广),该方法难以推广到正多胞体。基于正多面体群的抽象表示,提出了一种纯代数方法计算其矩阵生成元。因该方法完全是符号化的代数计算过程,可以类似推广到高维正多胞体,用于确定高维有限反射群的生成元。
正多面体;对称群;生成元;反射群
1 概述
由反射变换生成的反射群具有重要意义,其原因主要基于以下事实[1-4]:有一个一般性的理论框架覆盖它们;此类群包含物理化学领域的至关重要的点群(point group)为子群。Coxeter群是欧氏空间的有限反射群,它们是三维欧氏空间正多面体的对称群,或者是更高维欧氏空间正多胞体(regular polytopes)的对称群[5-8]。研究显示,此类对称群与量子物理、晶体化学、离散几何以及拓扑等领域有深刻交集,无论在理论层面还是应用领域,都具有深远意义[9-11]。
生成元是群的核心,它刻画了群的本质特征和发动机。为方便起见,本文把维欧氏空间及该空间上的有限反射群分别记为和。因正多面体的低维属性,借助几何模型,人们可以较容易地建立它们的生成元。但即便如此,正十二面体或正二十面体群生成元的确立还是相当复杂,这需要对它们的几何结构有非常深入的认识。因正多胞体无直观的真实几何模型,直接观察方法难以建立它们的生成元。
有鉴于此,本文提出一种纯代数的计算方法,用于确定3。该方法可以轻松推广到,给定的抽象表达式。本文将在探讨其几何意义的基础上,给出其生成元的纯代数计算方法。
2 G3抽象表示的几何意义
定义1 对称(symmetry)指的是物体的变换,该物体在此变换下保持不动。该物体的所有对称构成一个群,称为对称群(symmetry group)。
数学上,对称是一个等距变换,等距的含义与具体的测度有关[1]。
定义3 设一个离散对称群的生成元全部是反射变换,则称该群为完全反射群(reflection group)。
定义4 称一个多面体是规则的,如果它的每个面是相等的正多边形,且每个顶点都处于等价的地位。
为方便起见,下面介绍规则多面体的Schläfi标记[2]。记{}为正边形,{}表示规则多面体,它的每个面都是相同的{},且每个顶点有个相同的{}相交。可以证明,三维空间总共有5个规则多面体(或正多面体,柏拉图体),其简便推导方法可简述如下。设和是两个自然数,{}的每个立体角由个角度为围成。因立体角小于,因此,和应满足

图1 三维欧氏空间存在五个规则多面体
Fig.1 There are five regular solids in the three-dimensional Euclidean space

(a)正方体和正八面体互为对偶
(b) {,}的中心、顶点以及该顶点所在面的对边中点确定的平面是{}的反射面
图 2 正多面体对偶性及对称性说明
Fig. 2 The duality and symmetry of regular polyhedra

(3)
图3 具有[3,4](左)和[3,5] (右)对称性的球面拼砌图
Fig. 3 The spherical tilings with the symmetries of [3,4](left) and [3,5] (right)
在球面几何中,球面上两条测地线(geodesics,即大圆弧)的夹角等于经过测地线的平面的二面角。设和是两个法向量,给定经过原点的平面和,则这两个平面的夹角满足
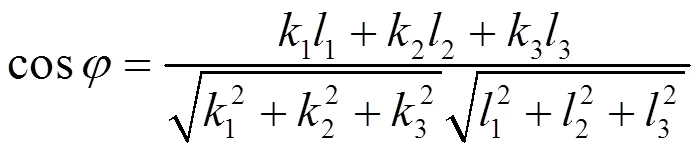
几何上看,两个反射变换的乘积是一个角度两倍于反射平面所构成二面角的旋转变换。据此,方程(2)的几何意义是,和的夹角分别是、和。球面三角形的面积可用角超(angular excess)度量:图3中的球面三角形面积为。任选一个这种三角形,在作用下,它的复制球面三角形可以完整地覆盖一次。因此,这种球面三角形称为在下的基本域(fundamental region)。因的面积为,反射群的阶数(order)
3 完全反射群生成元的代数计算方法


沿用上述思路,为清晰起见,下面分3小节,分别给出[3,3]、[3,4]和[3,5]的生成元。
3.1 [3,3]的生成元
3.2 [3,4]的生成元
3.3 [3,5]的生成元
[3,5]的对称性非常丰富,因它拥有一个异常复杂的生成元。理论上,仍可借助几何模型来确定其生成元,但这需要对和的几何结构非常了解。但用本文介绍的算法,却很容易可以获得[3,5]的生成元。
参考文献:
[1] Armstrong V E. Groups and symmetry[M]. New York: Springer-Verlag, 1987.
[2] Coxeter H S M. Generators and relations for discrete groups[M]. New York: Springer, 1980.
[3] Coxeter H S M. The complete enumeration of finite groups of the form[J]. J. London Math. Soc. 1935,1(1):21-25.
[4] Garling D J H, Gorenstein D, Dieck T,et al. Reflection groups and Coxeter groups[M]. Cambrideg:Cambridge University Press, 1990.
[5] Benson D J H. Polynomial invariant of finite groups [M]. Cambridge:Cambridge University Press, 1993.
[6] Mcmulle P, Schulte E. Abstract regular polytopes[M]. Cambridge:Cambridge University Press, 2002.
[7] Coxeter H S M. Regular polytopes[M]. New York: Dover, 1973.
[8] Humphreys J E. Geometry of Coxeter Groups[M]. Cambridge: Cambridge University Press, 1990.
[9] T. Hahn, International tables for crystallography[M]. Boston, MA: Kluwer Academic Publishers, 1996.
[10] Suck J B, Schreiber M, Haussler P. Quasicrystals: An Introduction to Structure[M]. Berlin: Springer-Verlag, 2002.
[11] Johnson D L. Symmetry[M]. London: Springer-Verlag, 2001.
A METHOD FOR THE GENERATORS OF THE SYMMETRY GROUPS OF REGULAR SOLIDS
*OUYANG Pei-chang, ZHAN Xiao-geng, DENG Zhi-yun, FANG Fa-ming
(School of Mathematics and Physics, Jinggangshan University, Ji’an, Jiangxi 343009, China)
According to the geometrical meaning of the regular solids, we can derive its matrix generators directly. However, it is difficult to achieve the generators of regular polytopes in higher dimension space for there are no visible models. Given an abstract presentation of a regular polyhedral group, we propose a pure algebraic method to establish its generators. The method can be similarly extended to deal with the regular polytopes in higher dimension space.
regular solids; symmetry group; generators; reflection group
1674-8085(2015)06-0008-04
TP391
A
10.3969/j.issn.1674-8085.2015.06.002
2015-07-06;修改日期:2015-08-30
国家自然科学基金项目 (11461035);江西省自然科学基金项目(20142BAB211012);井冈山大学博士科研启动基金项目(JZB1303);吉安市科技计划项目(吉市科计字[2014]36号12)
*欧阳培昌(1980-),男,江西赣州人,讲师,博士,主要从事计算机图形学研究(E-mail: g_fcayang@163.com);
占小根(1980-),男,江西上饶人,讲师,硕士,主要从事时间序列研究(E-mail: 63088664@qq.com );
邓志云(1976-),男,江西吉安人,副教授,硕士,主要从事组合数学研究(E-mail: danzhiyun163@163.com);
范发明(1971-),男,江西吉安人,讲师,主要从事组合数学研究(E-mail: famingfan@163.com).

