一类含分布时滞的随机Hopfield神经网络的指数稳定性
(四川师范大学 数学与软件科学学院,四川 成都60066)
张秀英,李树勇,赵 亮,杜启凤
众所周知,时滞无处不在,时滞的出现将导致系统的不稳定和振荡,同时,神经信号的传输也是一个受随机因素影响的充满噪音的过程,因此,含时滞随机Hopfield 神经网络模型解的稳定性分析是学者们关注的热点.各种分析方法被引入,如不等式技巧[1]、半鞍收敛定理[2-5]、Lyapunov 泛函法[6-9]、Razumikin 方法[10]、线性矩阵不等式[11]等判别稳定性的一些条件被建立. 半鞍收敛定理作为研究时滞随机系统矩稳定的有力工具,自Steve 等[2]将其引入时滞随机微分系统稳定性研究,给出含有界时滞的随机Hopfield 神经网络模型解几乎必然指数稳定的充分条件以来,发挥了很好的作用,许多稳定性结论利用这一思想而建立.基于此,本文中将运用半鞍收敛定理研究含离散和分布时滞的随机Hopfield 神经网络的稳定性. 通过构造一个恰当的Lyapunov 泛函并使用不等式分析技巧,给出该系统平凡解均方指数稳定和几乎必然指数稳定的一个新的充分条件.
1 准备知识
本文考虑如下一类含分布时滞的随机Hopfiled 神经网络系统:

其中,i∈Λ={1,2,…,n}表示第i 个神经元;x(t)=(x1(t),…,xn(t))T,xi(t)表示第i 个神经元在t 时刻的状态;C=diag{c1,…,cn},ci>0 表示在与神经网络不连通并且无外部附加电压差的情况下,第i 个神经元恢复孤立静息状态下的速率.A=(aij)n×n,B=(bij)n×n和D =(dij)n×n表示神经元相互连结的权矩阵.h(x(t))=(h1(x1(t)),…,hn(xn(t)))T∈Rn,g(x(t-τ))=(g1(x1(t -τ1)),…,gn(xn(t -τn)))T∈Rn,f(x(t))=(f1(x1(t)),…,fn(xn(t)))T∈Rn,其中hi,gi和fi表示外部激活函数.k(t)=(kij(t))n×m,这里kij(t)是时滞核函数.初值ξ(t)=(ξ1(t),…,ξn(t))T,ξi(t)是定义在(-∞,0]上的有界连续函数,且(θ)|,τj是常数,且是噪音强度矩阵. w(t)=(w1(t),…,wm(t))T是定义在完备概率空间(Ω,F,P)上的m-维Brownian 运动,其自然域{Ft}t≥0建立在{w(s):0≤s≤t}上.
记Rn上的Euclidean 范数为|◦|,E(◦)代表数学期望算子.
对系统(1)或(2),假设:
(H1) fj,gj,hj和σij是Lipschitz 连续的,Lipschitz 常数分别为βj>0,αj>0 ,γj>0 和Lij>0,且fj(0)=gj(0)=hj(0)=σij(0)=0 且fj有界,其中i,j∈Λ.
(H2) kij(t)是定义在[0,+∞)上的实值连续函数,且满足:

在上述假设下,当t≥0 时,系统(1)或(2)有唯一的全局解[12],用x(t,ξ)或x(t)表示.在假设(H1)下,系统(1)或(2)有零平凡解.
定义1 系统(1)或(2)的平凡解是几乎必然指数稳定的,如果对任意解x(t),满足:

定义2 对系统(1)或(2),如果存在正常数λ 和K 以及任意初始值ξ,使得

即有

成立,则称系统(1)或(2)是均方指数稳定的,λ 叫做系统(1)或(2)的解的2 阶Lyapunov 指数.
引理1 (半鞍收敛定理)[12](Th.3.9,P.14).设A(t)和U(t)是t≥0 上的两个连续适应增随机过程,且几乎必然有A(0)=U(0)=0.又设M(t)是一个实值连续局部棋,且几乎必然有M(0)=0.设ξ 是一个非负F0可测随机变量且满足Eξ <∞.对t≥0,设

若X(t)非负,则
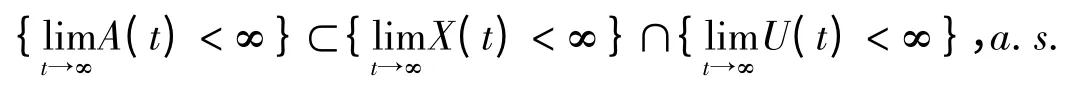
这里B⊂D,a.s.意味着P(B∩Dc)=0.特别地,若,则对几乎所有的ω∈Ω,有

引理2 对具有适当维数的任意向量x,y 及任意对称正定矩阵H >0,有:

2 主要结果
定理 对系统(1)或(2),如果存在正定对角阵P=diag{p1,…,pn},Q=DP-1DT=(qij)n×n,对所有i∈Λ={1,2,…,n},满足:

则系统(1)或(2)是几乎必然指数稳定的和均方指数稳定的.
证明:由条件(H3),存在μ >0,使得:

由Itôs 微分,得:

由引理2,有

所以,

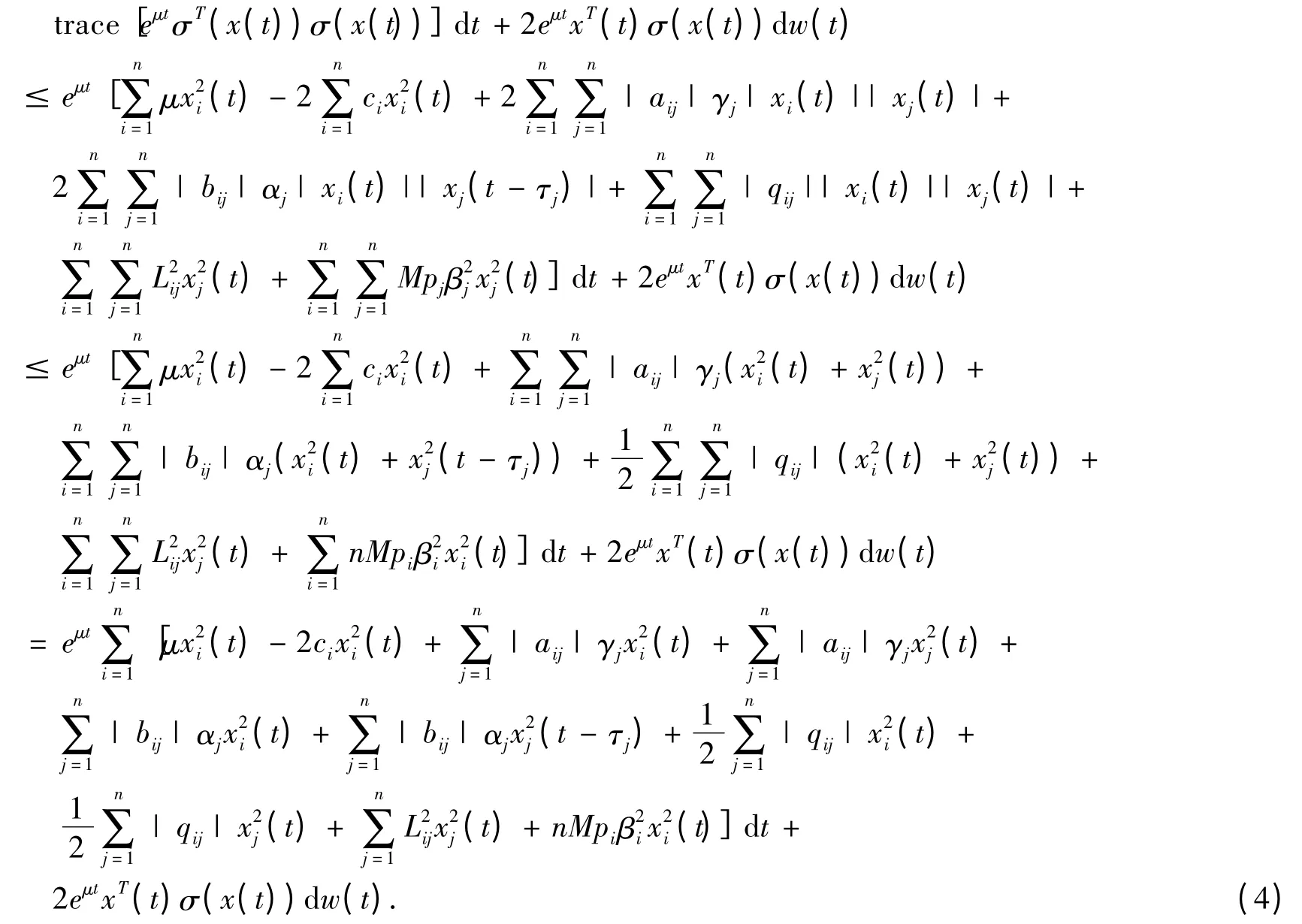
从0 到t 积分,可得

又因为,

所以,

由假设(H1)和(H2)可知,

因此,V(0,x(0))有界,且(5)式右边是非负半鞅.由引理2.1 可知,

又

因此,

即
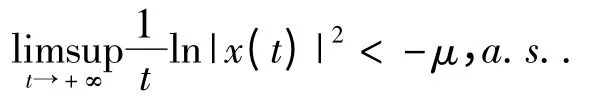
对(5)式两端同时取期望,得

即
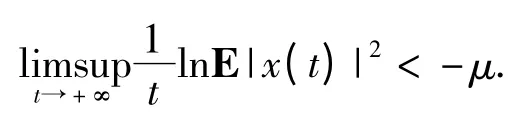
证毕.
3 应用举例
本节通过一个例子,阐明结果的有效性.
例 考虑如下二维含分布时滞的随机Hopfield 神经网络系统

这里h1(v)=h2(v)=arctanv,f1(v)=f2(v)=(ev-e-v)/(ev+e-v),kij(t)=e-t,i,j =1,2.A =(aij)2×2,a11=1,a12=2,a21=3,a22=1;C=(cij)2×2,c11=14,c12=0,c21=0,c22=9;D=(dij)2×2,d11= -3,d12=1,d21=2,d22= -2;L=(lij)2×2,l11=4 ,l12=1,l21=1,l22=1.这样= -3/8.
取P=(pij)2×2,p11=1,p12=0,p21=0,p22=1,γi=βi=1(i=1,2).从而Q=(qij)2×2=DP-1DT,其中q11=-1/2,q12=0,q21=0,q22=1.取经计算,知
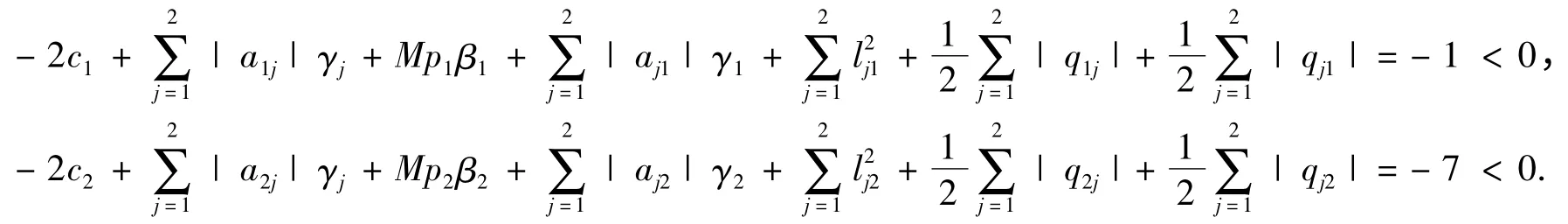
因此本文定理所需条件成立,进而由本文定理,系统(6)的解是均方指数稳定的.
通过数值模拟,得到系统(6)的解x(t)=(x1(t),x2(t))T变化趋势图(图1),可看到该系统的解是均方稳定的.这与本方法所得结论吻合.

图1 系统(6)解的变化趋势Fig.1 The change trend of solution of the system (6)
[1] LI W,SUN J. Mean Square Exponential Stability Analysis of Stochastic Delayed Hopfield Neural[J]. Physics Letters A,2000,13:745 -753.
[2] BLYTHE S,MAO X,LIAO X. Stability of Stochastic Delay Neural Networks[J]. Journal of the Franklin Institute,2001,338(4):481 -495.
[3] ZHOU Q,WAN L. Exponential Stability of Stochastic Delayed Hopfield Neural Networks[J]. Applied Mathematics and Computation,2008,199(1):84 -89.
[4] HUANG C,CHEN P,HE Y,et al. Almost Sure Exponential Stability of Delayed Hopfield Neural Networks[J]. Applied Mathematics Letters,2008,21(7):701 -705.
[5] MENG X,TIAN M,HU S. Stability Analysis of Stochastic Recurrent Neural Networks with Unbounded Time-varying delay[J].Neurocomputing,2011,74(6):949 -953.
[6] BALASUBRAMANIAM P,RAKKIYAPPAN R. Global Asymptotic Stability of Stochastic Recurrent Neural Networks with Multiple Discrete Delays and Unbounded Distributed Delays[J]. Applied Mathematics and Computation,2008,204(2):680 -686.
[7] GUO Y. Mean Square Global Asymptotic Stability of Stochastic Recurrent Neural Networks with Distributed Delays[J]. Applied Mathematics and Computation,2009,215(2):791 -795.
[8] WANG Z,LIU Y,LIU X. On Global Asymptotic Stability of Neural Networks with Discrete and Distributed Delays[J],Physics Letters A,2005,345(1):299 -308.
[9] LI H,CHEN B,ZHOU Q,et al.Robust Exponential Stability for Uncertain Stochastic Neural Networks with Discrete and Distributed Time-varying Delays[J]. Physics Letters A,2008,372 (19):3385 -3394.
[10] 胡 建,李树勇,杨治国. 含混合时滞的随机Hopfield 神经网络模型的全局指数稳定性[J]. 四川师范大学学报(自然科学版),2012,35(3):303 -308.
[11] BALASUBRAMANIAM P,RAKKIYAPPAN R. LMI Conditions for Stability of Stochastic Recurrent Neural net-works with Distributed Delays[J]. Chaos Solition and Fractals,2009,40(4):1688 -1696.
[12] MAO X R. Stochastic Differential Equations and Applications[M].Chichester:Horwood Publishing,1997.

