带有Neumann边界条件和非局部反应项的非局部扩散方程的爆破
李佳贤,杜宛娟
(西华师范大学 数学与信息学院,四川 南充 637009)
0 引言和主要成果
本文主要研究以下非局部扩散问题的爆破现象

其中,α >0,Ω 是一个有界连通光滑区域,核函数J:RN→R 是一个具有紧支集的非负有界连续对称函数初值u0(x)是非负,非平凡的有界函数.问题(1)经常出现在人口密度、化学反应和热传递等物理模型中.比如u(x,t)可以表示单一种群在空间点x 和时间t 时的密度,J(x -y)可以看作是种群从位置y 转移到位置x 的概率分布,卷积(J* u)(x,t)=表示个体从其他位置到达位置x 的速率,而则表示离开位置x 到达其他位置的速率.非局部反应项J* eαu(x,t)表示了单一人口密度在区域Ω 内呈指数增长.在考虑内源的情况下,密度u满足非局部扩散方程(1).在问题(1)中,积分仅仅是在Ω 上进行的,而∫J(x - y)(u(y,t)- u(x,t))dy 考虑了个体到达或离开位置x 的情况,因此,把这种扩散仅仅限定在Ω 上进行,没有个体进入或离开这个区域.从而问题(1)具有Neumann 边界条件,参见文献[1].
近年来,具有ut=∫RNJ(x -y)u(y,t)dy -u(x,t)这种形式的非局部扩散问题,以及它的一些变式,被广泛应用于扩散问题的建模,可以参考文献[2 -8].
现在给出这篇文章的主要成果.
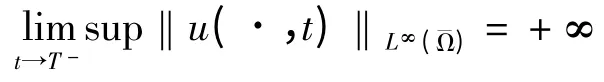
且在Ω 上满足下面这个恒等式

确定了解的存在性和唯一性,接下来去研究解发生爆破时的时间和速度.

与之相关的爆破率,有:
定理3 假设u 是问题(1)的解,且在时刻T 爆破,则:

1 解的局部存在性
这部分主要给出定理1.1 的证明,并通过Banach 不动点定理来证明解的存在性和唯一性.为此,给出一些必要的准备.固定t0>0,令Banach 空间其范数定义为:

定义算子T:Xt0→Xt0

问题(1)的解将在Xt0的一个适当的球中,通过上面算子的一个不动点得出.将通过下面这个引理说明算子T 是有定义的,并且给出条件保证它是严格紧缩的.
引理1 算子T 是有定义的,且从Xt0映到Xt0.令那么,存在一个正常数C =C(α,‖w‖Xt0,‖z‖Xt0,K,Ω),使得

若t0足够小,则Tw0在球是严格紧缩的.
证明:首先验证Tw0是从Xt0映到Xt0.对于有:

所以Tw0(w)在t=0 处连续.对于,满足

则Tw0在(0,t0]上连续.
由于核函数J 在空间中是一致连续的,因此Tw0(w)是x 的连续函数.对则Tw0(w)于是Tw0(w)是从Xt0映到Xt0.

其中η≤max{‖w‖Xt0,‖z‖Xt0}.由(x,t)的任意性可得估计(4)式.
选取t0使得Ct0<1,令w0=z0,那么在里,(4)式确保算子Tw0是严格紧缩的.实际上,w 和z 定义在这样的球中可以得到因此,存在一个仅仅依赖于J 和u0的常数C,使得
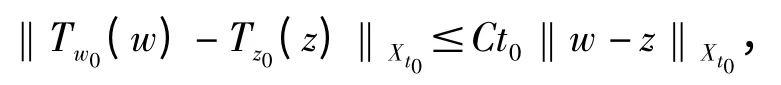
对此可以选取t0使得Ct0<1/2 保证在球内是严格紧缩的.
定理1 的证明(存在性与唯一性):由Banach 不动点定理和引理1 可以得到问题(1)的解在[0,t0]上是存在且唯一的.如果‖u‖Xt0<∞,令初值对于t1>t0,可以将解延拓到区间[0,t1),和前面的证明类似.因此,若解存在一个最大时间T,是有限的,那么解在范数下爆破,即

从方程(1)中可以得到u 满足下面的恒等式
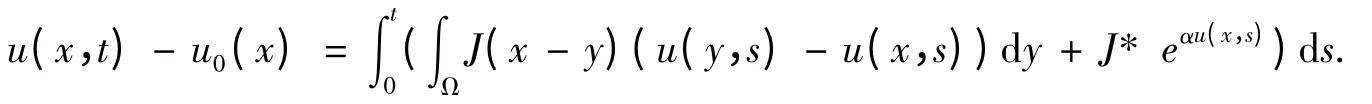
在等式两边对x 积分并运用Fubini 定理,则有

定理1 得证.
为了说明问题(1)的解满足比较原理.为此,先介绍上解和下解.
下解的定义和上解的定义类似,只需将上面的≥全部换为≤.
现在给出与上解和下解有关的比较原理和极值定理两个引理.证明参见文献[9].
2 爆破与爆破率
定理2 的证明:在方程(1)两边对x∈Ω 积分,运用Fubini 定理和Jensen 不等式,可得到:

所以∫Ωu(x,t)dx 不是全局存在的,则u 也不可能全局存在.通过定理1 可知,解u 在范数下爆破.在上式不等式积分中,可以得到对爆破时间的一个估计,即:

现在我们给出爆破率,即对定理3 进行证明.

对(5)式在(t,T)上积分,可得:

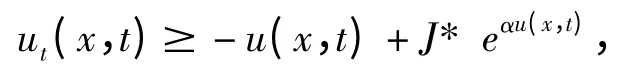
由于u(x,t)爆破,则存在t0使得对于任意的t∈(t0,T),存在参数ε >0,使得

在(t,T)上积分,可得

令ε→0 时,由(6)和(7)式可得:
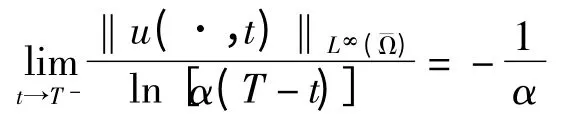
即定理得证.
[1] CORTAZAR C,ELGUETA M,ROSSI J,et al. Boundary Uxes for Non-local Diffusion[J]. Journal of Differential Equations.2007,234(2):360 -390.
[2] ANDREU F,MAZON J,ROSSI J,et al. The Neumann Problem for Nonlocal Nonlinear Diffusion[J]. Journal of Evolution Equations. 2008,8(1):189 -215.
[3] ANDREU F,MAZON J,ROSSI J,et al. Local and Nonlocal Weighted P - Laplacian Evolution Equations with Neumann Boundary Conditions[J]. Publicacions Mathematiques. 2011,55(1):27 -66.
[4] GALAKTIONOV V,VAZQUEZ J. The Problem of Blow -up in Nonlinear Parabolic Equations[J]. Discrete and Continuous Dynamical Systems. 2002,8(2):399 -434.
[5] IGNAT L,PINASCO D,ROSSI J,et al. Decay Etimates for Nonlinear Nonlocal Diffusion Problems in The Whole Space[J].Journal d'Analyse Mathematique. 2014,122(1):375 -401.
[6] MAZON J,ROSSI J,TOLEDO J. On Nonlinear Nonlocal Diffusion Problems[J]. International Journal of Biomathematics &Biostatistics. 2010,1:181 -192.
[7] SAMARSKI A,GALAKTIONOV V,KURDYUNOV S,et al. Blow -up in Quasilinear Parabolic Equations[M]. Walter de Gruyter,Berlin. 1995:560.
[8] WANG M. Blow-up Rate Estimates for Semilinear Parabolic Systems[J]. Journal of Differential Equations. 2001,170(2):317 -324.
[9] CORTAZAR C,ELGUETA M,ROSSI J,et al. How to Approximate The Heat Equation with Neumann Boundary Conditions by Nonlocal Diffusion Problems[J]. Archive for Rational Mechanics and Analysis. 2008,187(1):137 -156.

