一类完全由内积构造的多任务核的几个性质
刘建强
(宁夏大学数学计算机学院,宁夏银川750021)
1 问题的提出
多任务核的泛函分析框架由C.A.Micchelli等提出[1-2].我们首先介绍多任务核的概念.
假设X是一个集合,Y是一个实希尔伯特空间,对任何y,z∈Y,其内积记为 <y,z>,H为从X到Y的映射组成的线性空间.用L(Y)表示所有从Y到Y的有界线性算子,对于任何A∈L(Y),用 表示其共轭算子,L+(Y)表示所有非负有界算子,即任何A∈L+(Y),<y,A(y)>0.
定义1 称算子K:X×X→L(Y)为一个多任务核,如果
(A1)对任何 t1,t2∈ X,K(t1,t2)∈ L(Y),K(t1,t2)=K(t2,t1)*;
(A2)对任何自然数 m,tj∈ X,yj∈ Y,1≤ j≤ m,都有

如果多任务核K(·,·)同时是从X×X到L(Y)的一个有限秩算子,则称其为有限秩多任务核.传统的再生核是多任务核的一部分,下面将传统的再生核称为标量值核.在文献[3]中,给出了如下的有限秩多任务核的刻画定理.
定理1 设φj(t)是X上的函数,1≤j≤m.有限秩算子
关于乘积的多任务核的构造是考虑这样的问题:对t1,t2∈X,K1,K2,K是关于t1,t2的多项式,K是一个多任务核且K1(t1,t2)K2(t1,t2)=K(t1,t2),则K1,K2是否为多任务核?本文将讨论输入空间中两个元素t1,t2内积x=(t1,t2)的多项式所构成的多任务核.这时,多任务核的特征矩阵C为对角矩阵,要成为多任务核,只需要系数为非负值.因此,在下文中,令
f1(x)=K1(t1,t2),f2(x)=K2(t1,t2),f(x)=K(t1,t2).
则上述问题变成:
多项式f1(x),f2(x),f(x)的首项系数均为1,f(x)所有系数均非负,是否至少有一个fi(x)(i=1或2)系数均非负,或f1(x),f2(x)系数均可为负数?
定理2 K1,K2必有其一为多任务核,如果下面的条件之一成立:
定理3 设f1(x)=x2-px+q,p>0,q>0,f2=n.是否存在K2使得K为多任务核的条件仅与p2/q的值有关.记在f1=n时,存在K2使得K为多任务核的p2/q最大数为θn,则θn是关于n的单调增数列.
2 定理2的证明
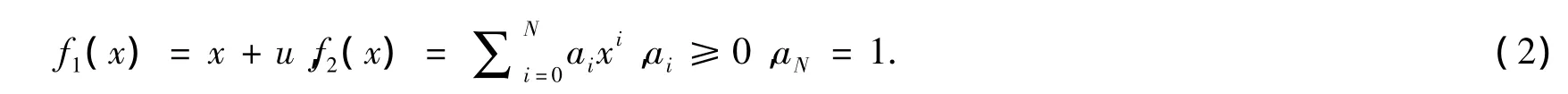
考虑乘积的各项系数必须为非负且首项系数为正,uai+1+ai≥0,i=0,…,N-1.若u=0,根据参考文献[3]多任务核的平移性质得知K2是多任务核;若u<0可以推出ai>0,因此K2是多任务核;若u>0,K1是多任务核.故K1,K2至少有一个为多任务核.

根据定理1可得不等式组
先考虑q<0的情况,这时由不等式组(4)第一式得到a0<0,结合不等式组(4)第三式得pa1>0,再结合不等式组(4)最后一式得p>0,a1>0,因此qa1+pa0<0,而这与不等式组(4)第二式矛盾.
再考虑q=0的情况,这时f中含有因子x,根据多任务核平移性质,K/x仍然是多任务核,而这将回到f1=1的情况,可以证明K1,K2中至少有一个为多任务核.
最后考虑q>0的情况.这时如果p<0,从不等式组(4)第一式解得a0>0,第四式得到a1≥-p>0,这时K2是一个多任务核.在q>0且p≥0时K1已是多任务核.
3 定理3的证明
证明 首先,证明是否存在K2使得K为多任务核的条件仅与p2/q的值有关.事实上,取θ=p2/q,则f1(x)/p2=(x/p)2-(x/p)+1/θ,是否存在K2使得K为多任务核的条件与x2-x+1/θ相同,而后者仅与θ的取值有关.
接下来用数学归纳法证明θn为单调增数列.n=1时,设
f2(x)=x+a0,f1(x)f2(x)=x3+(a0-p)x2+(q-a0p)x+a0q.
这要求a0≥p,a0≤q/p。要使a0有解则需要p2/q≤1.也就是说,当p2/q>1时不存在K2使得K为多任务核,即命题对n=1时成立,且由定义有θ1=1.
当n=2时,设 f2(x)=x2+a1x+a0,由(4)知 a1,a0需满足qa0>0,qa1-pa0≥0,-pa1+q+a0≥0,-p+a1≥0.
要使a1有解则需要p2-q≤a0,(p2-q)a0≤q2.由于θn是寻求满足条件的最大数,故假设p2>q寻求a0的解(无解时可设p2≤q继续求解).这时若要a0有解则需要(p2-q)2≤q2,解得p2/q≤2,也就是说,当p2/q>2时不存在K2使得K为多任务核,即命题对n=1时成立,且由定义即得θ2=2.
对更一般的情况,假设对小于n的情况命题都是成立的,也即对所有k<n,找到了θk,当p2/q>θk时,不存在K2使得K为多任务核.
现证明对于n的情况也成立.考虑乘以一个正常数不改变是否为多任务核的性质,不妨设
K1(t1,t2)=f1(x)=qx2-px+1,
K2(t1,t2)=f2(x)= αn-1xn-1… + α1x+1,
K3(t1,t2)=f3(x)= αnxn+an-1xn-1+ … + α1x+1.
这样就有
f1(x)/q=x2-p/qx+1/q且(p/q)2/(1/q)=p2/q.
考虑到一个正数倍不影响是否为多任务核,因此这里θn仍定义为p2/q可能的最大值.为使K2,K3成为多任务核,需满足的条件分别为

易见,不等式组(5)和(6)中部分式子相同.下面对比两组不等式中不同的部分,即考虑不等式组(5)最后两式和不等式组(6)最后三式.
从不等式组(6)看,最后一式表明 αn> 0,由倒数第二式知 αn≤qαn-1/p,由倒数第三式知 αn≥ pαn-1-qαn-2,要使 αn有解则需要 αn-1> 0 且(p2- q)αn-1≤pqαn-2.考虑到 θn是上界,故只需在 p2-q > 0 时找到合适的θn即可.根据归纳假设,p2-q=0对应θn=1的情况,在n=1时已经达到,即p2-q>0.由此可得不等式

从不等式组(5)看,其最后一式表明αn-2>0,再由其倒数第二式可得

因此,为了使不等式组(5)有解,要求αn-2>0.至此,不等式组(5)和(6)的不同要求在于(7)和(8).然而,将这两不等式的右端相减,得到
pqαn-2/(p2-q)- qαn-2/p=q2αn-2/p/(p2-q)> 0.
因而,(7)上界大于(8)上界,也就是说,在不等式组(6)中αn-1被允许的存在范围大于其在不等式组(5)中的存在范围.由于其他条件相同,因此不等式组(6)刻画的条件较不等式组(5)更加宽松,或者说不等式组(5)刻画的条件满足不等式组(6),因此θn≥θn-1.
根据归纳法原理,对于所有的自然数n,有θn≥θn-1.
4 θn的计算
可以看出,所有θn都由对应于不同n的不等式组(5)解出.事实上,将所有αk按照k减小的次序消去,得到一个关于θ的方程gn(θ)=0,而θn则是这个方程的最大根.篇幅所限,这里仅列举当n≤4时,gn(θ)的表达式及θn的值如下:
g1(θ)= θ- 1;g2(θ)= θ- 2;g3(θ)= θ(θ- 2)2-1;g4(θ)= θ5-7θ4+17θ3-17θ2+6θ.
θ1=1,θ2=2,θ3=(3+)/2,θ4=3.
[1]Micchelli C A,Pontil M.On learning vector- valued functions[J].Neural Computation,2005(17):177 -204.
[2]Caponnetto A,Micchelli C A,Pontil M,Ying,Yiming:Universal multi- task kernels[J].J.Mach.Learn.Res,2008(9):1615-1646.
[3]Liu Jianqiang,Micchelli C A,Wang Rui,et al.Finite rank kernels for multitask learning[J].Advances in Computational mathematics,2014,38(2):427 -436.

