数值分析实践教学实验设计

王同科，　常慧宾，　王彩华

(天津师范大学数学科学学院，天津300387)



数值分析实践教学实验设计

王同科，常慧宾，王彩华

(天津师范大学数学科学学院，天津300387)

[摘要]简述了数值分析课程实验设计的总体思路，设计了三个新的探索性实验，包括递归方程拟合、非光滑函数插值和奇异积分计算.这些实验均从最简单的情形出发，通过观察、比较、分析和联想得出了新的结论，有助于培养学生的创新思维能力，为更好地开展数值分析实践教学提供指导.

[关键词]数值分析； 递归方程拟合； 非光滑函数插值； 奇异积分计算； Mathematica软件

1实验设计综述

数值分析研究数值求解数学问题的方法和理论，是一门理论与实践并重的课程.在数值分析教学中，实践环节对于培养学生运用知识的能力和创新能力之重要性已成为高校教学上的共识，因此各个学校普遍设置了数值分析实验环节，安排每周1至2学时的上机实习.如何有效地利用有限的实验课时,使学生真正掌握数值分析的基础，如何争取更多时间引导学生深入地探索与实验，很多学校进行了有益尝试.文[1]综述了三峡大学数值分析课程教学改革的研究成果，文[2]总结了中南大学以MATLAB 为平台进行数值分析课程辅助教学的方法，文[3，4]主张采用现代信息网络进行数值分析实验教学，文[5，6]分别指出了数值分析教学中存在的问题，特别提出应根据不同学校的学生特点改革教学内容，加强实验教学.这些研究成果为各个学校的数值分析教学提供了有益的参考.

在数值分析增设实验课时的同时，很多学校同步开设了数学实验和数学建模课程.这三门课程相互融合、互为补充，使数学教学从纯理论迈向了以理论为主，兼顾实践的阶段，共同促进了学生实践能力的提高[7，8].从实验设计的角度出发，但琦等[9]将数学实验分为基础性实验和综合性实验，而基础性实验包含验证性实验和计算性实验；综合性实验包含探索性实验和应用性实验.这种分类方法对于数值分析实验同样适用，早期的数值分析实验主要是基础性实验，要求学生编写常用算法的C语言或Fortran语言程序；近些年，则普遍引入了通用数学软件，程序编写的难度大大下降，有更多的时间安排一些综合性实验，学生更有兴趣，学习效果有了很大提高[10].

随着计算机性能的不断提高，计算机代数系统(CAS)已经发展到了高度智能化的水平，符号运算与数值计算的边界越来越模糊，二者的有机融合催生了许多高效率的算法.对于数值分析实践教学来说，应该乘势而为，适度引入符号运算，通过符号运算与数值计算结果的对比分析，比较数值算法的优劣，看清数值算法的本质或借助符号运算，提高数值方法的计算效率.在这方面,我们已经设计了一些实验,如Chebyshev多项式降阶实验, 二次插值函数一阶导数超收敛点实验, 列主元Gauss消去法增长因子实验等,均已收录到了教材: Mathematica与数值分析实验[11]中.这本教材围绕算法这一主题展开，用算法的实现、算法的理解、算法的应用这一主线将各部分内容有机地串联在一起，实验内容涵盖了数值分析例题选解、基础算法实验、数值方法探索性实验和数值方法应用性实验.目前该教材已被一些学校采用，收到了良好的效果.

在数值分析实验设计环节，基础性实验内容相对固定，应用性实验则有大量的数学模型案例可供选用，而探索性实验则相对缺乏.除了在教材[11]中给出的一些探索性实验外，近几年，结合科研工作，我们又设计了一些新的探索性实验，下面给予简单介绍.

2几个典型的探索研究性实验

2.1递归方程拟合

题目设an+1=an+1/an，a1=1，给定一些n，画出(n,an)的散点图，并寻找合适的函数拟合以上图形.

分析与求解本题给出的公式实际是一个非线性的差分方程，可以尝试使用Mathematica8.0的RSolve命令求解，但无法成功求出问题的解.下面采用拟合方法求该差分方程的近似解，由于an+1=an+1/an本质上是一个不动点迭代，采用NestList命令计算一些n对应的an值，Mathematica程序为

g[x_]:=x+1.0/x; (*定义迭代函数*)

nt = 5000; x0 = 1; (*n=nt=5000*)

t = NestList[g, x0, nt] (*计算前5 000个n对应的an值，并存放在表t 中*)

p1=ListPlot[t, PlotStyle -> {PointSize[Small], Red}, AxesStyle -> Thick, BaseStyle -> {Bold, FontSize -> 15}, AxesLabel -> {n, Subscript[a, n]}](*绘制散点图，如图1所示*)

图1　(n,an)的散点图

由图1可知，an随n单调增加，观察图像可以考虑使用对数函数或指数函数进行拟合.经测试，指数函数拟合效果较好，拟合命令为 FindFit[t,a*n^b,{a,b},n].执行该拟合命令得拟合公式为

f(n)=1.42034n0.499504，

拟合误差

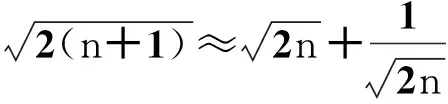
对于本实验，得到f(n)=1.42034n0.499504并不困难，进一步的推导实际是一个探索发现的过程，需要充分发挥我们的想象力.

2.2非光滑函数插值

题目1. 给定函数

2. 将f1(x)和f2(x)分别在x=0点做Taylor展开，比较它们有什么不同？

3. 当n=2时，对于函数f1(x)，使用其Taylor展开式中的基函数构造插值函数，计算插值最大误差，并与二次插值多项式进行比较.

4. 将区间[0,1]剖分为n=4等份，求f1(x)的四次插值多项式，并使用其Taylor展开式中的基函数构造插值函数，计算插值最大误差，与n=2时的插值进行比较，观察误差的变化情况.

分析与求解1. 当n=2时，插值节点为xk=k/2,k=0,1,2，直接使用二次Lagrange插值公式，得

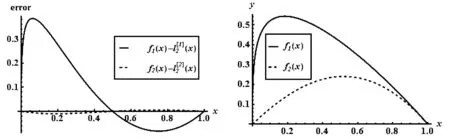
图2　fi(x)的插值误差图形(左)和函数图形(右)

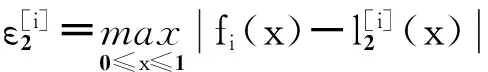
使用Mathematica的NMaximize命令可知，

进一步绘出f1(x)和f2(x)的函数图形，见图2右图，可见两个函数的值相差并不大，是什么原因导致插值的逼近效果有这么大的差别？联想到插值余项公式

仔细观察图2右图，可知函数f1(x)在x=0点的光滑性较差，原因正在于此.

2. 直接使用Mathematica的Series命令将f1(x)和f2(x)分别在x=0点做Taylor展开，如对于f1(x)，命令为s1[x_]=Series[f1[x],{x,0,4}]，得

(1)

可得插值函数

图3　两种插值的误差图形

4. 当n=4时，插值节点为xk=k/4,k=0,1,…,4，可求得f1(x)的四次Lagrange插值多项式

若使用f1(x)的分数阶Taylor展开式(1)中的基函数，则得

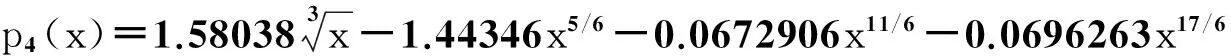
计算插值最大误差，连同n=2的结果，一起列在表1中.

表1　n=2和n=4时f1(x)的两种插值最大误差

由表1知，当插值节点增加时，f1(x)的多项式插值精度并没有明显提高，而其分数阶插值精度则有数量级的提高.

本实验中f1(x)在x=0点的导数不存在，这虽然仅是函数的一个局部性质，但它对于插值精度的影响则是全局的.对于这种局部非光滑函数，通常的多项式插值并不能准确地反映出函数的这种非光滑性质，因而逼近效果往往比较差[12].若使用非光滑函数做插值基函数，则可以大大改善插值精度，但插值基函数的种类繁多，需正确选择.基本方法是将函数在不可导点做广义的Taylor级数展开[12]，使用该展开式的基函数构造插值.这种级数展开通常归结为符号计算，本实验是符号计算与数值计算联合使用提高算法精度的一个典型例子.实验中的分数阶插值采用了简单的待定系数方法，更一般的构造方法及误差估计见文[13].

2.3奇异积分计算

题目1. 设定计算精度ε=10-8，用Romberg算法计算积分

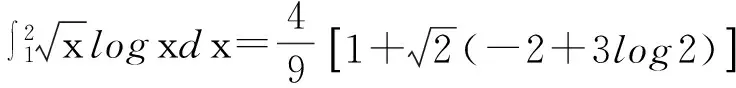
统计外推次数及函数值计算个数，该方法对于这两个积分计算效率高吗？

2. 查找资料，写出复合梯形公式的误差渐近展开式，从理论上解释上面积分计算快或慢的原因.

3. 修改Romberg算法，使之对第一个积分有更高的计算效率.

分析与求解1. 设f(x)∈C[a,b]，将区间[a,b]划分为n等份，记

h=(b-a)/n，xi=a+ih，i=0,1,2,…,n，

(2)

复合梯形公式单独使用时计算精度不高，通常情况下可以使用Romberg算法进行外推.Romberg算法通过对不同步长的复合梯形公式进行组合，逐步消去误差低阶项达到快速收敛的目的.Romberg算法公式为

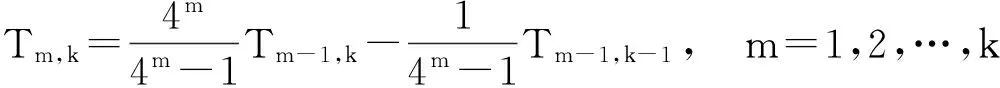
其中T0,k表示区间[a,b]二分k次后求得的梯形值，Tm,k表示外推m次的加速值.

表2　Romberg算法计算两个积分的结果统计

由表2知，Romberg算法可以计算这两个积分，积分②计算正常，但积分①外推收敛很慢，计算效率非常低.为什么同一个函数在不同区间上的计算效果差别如此之大呢？注意到Romberg算法外推的理论基础是复合梯形公式的误差渐近展开式，我们需要从误差渐近展开式出发进行讨论.

2. 当被积函数f(x)在积分区间上充分光滑时，梯形公式(2)的误差渐近展开式为[11]

(3)

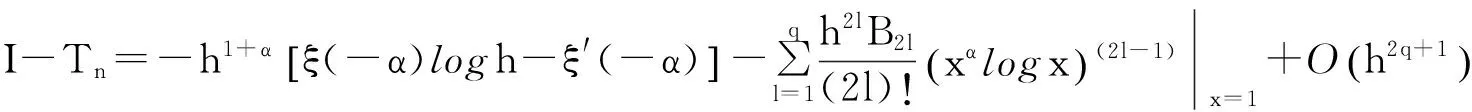
(4)

进一步，有

接下来进行正常外推即可.这种方法称为改进的Romberg算法.

Romberg外推算法是数值分析的一个必做实验，通常仅对充分光滑函数进行，计算效率很高，学生除了练习编程之外，难有其他收获.此实验通过奇异积分计算，开阔学生思路，让学生认识到，在实际计算时针对具体函数正确选用算法或改进现有算法十分重要，其基础是算法的理论分析.在数值分析学习中，理论与实践同等重要，缺一不可.学生通过完成实验还可以体会科学探索的过程，如有兴趣，还可以进一步学习奇异积分的误差渐近展开式及其推导过程[15,16].

3结论

在数值分析教学中开设上机实验课早已成为各个高校的共识，但设置何种实验则讨论较少，特别是探索创新型实验更少.本文设计了三个新的数值分析实验，这些实验是相关基础实验的深化和推广，有助于学生加深对所学数值方法的理解.学生通过完成实验，可以有效地提高科学计算能力.

[参考文献]

[1]杜廷松.关于《数值分析》课程教学改革研究的综述和思考[J].大学数学,2007,23(2):8-15.

[2]万中,韩旭里.《数值分析》课程教学的新认识及改革实践[J].数学教育学报,2008,17(2):65-66.

[3]吴勃英,王勇,石振锋.《数值分析》实验课网络实验平台建设体会[J].大学数学,2007,23(3):13-14.

[4]谢治州.“数值分析”实验教学的实践与探索[J].实验室研究与探索,2010,29(5):133-136.

[5]殷明,朱晓临,陈晓红,陈国琪.计算方法课程改革的设想与实践[J].大学数学,2006,22(5):15-17.

[6]刘徽,黄宽娜.计算方法课程教学改革的探索与实践[J].西南师范大学学报(自然科学版),2013,38(6): 183-187.

[7]周金明,朱晓临,张伟.结合数学建模,改革《数值分析》教学[J].大学数学,2013,29(5):13-17.

[8]温一新,王涛.数学实验和数学建模教学中数学软件应用的实例分析[J].大学数学,2014,30(5):26-30.

[9]但琦,杨廷鸿,吴松林,付诗禄,林琼.论大学数学实验课的教学设计[J].大学数学,2010,26(5):1-5.

[10]何亚丽,刘春凤.数值计算方法课程中实验环节的设计[J].大学数学,2008,24(1):9-12.

[11]王同科,张东丽,王彩华.Mathematica与数值分析实验[M]. 北京：清华大学出版社,2011.

[12]王同科,佘海艳,刘志方.分数阶光滑函数线性和二次插值公式余项估计[J].计算数学,2014,36(4):393-406.

[13]樊梦,王同科,常慧宾.非光滑函数的分数阶插值公式[J].计算数学,2016,38(2):212-224.

[14]李庆扬,王能超,易大义.数值分析(第五版)[M].北京：清华大学出版社,2008.

[15]Sidi A. Euler-Maclaurin expansions for integrals with endpoint singularities: a new perspective[J]. Numerische Mathematik, 2004, 98(2): 371-387.

[16]Wang Tongke, Li Na, Gao Guanghua. The asymptotic expansion and extrapolation of trapezoidal rule for integrals with fractional order singularities[J]. International Journal of Computer Mathematics, 2015, 92(3): 579-590.

Experimental Design for Practical Teaching in Numerical Analysis

WANGTong-ke,CHANGHui-bin,WANGCai-hua

(School of Mathematical Sciences, Tianjin Normal University, Tianjin 300387, China)

Abstract:Based on reviewing the basic ideas for experimental design in numerical analysis, this paper designs three new exploratory experiments, including fitting for a recurrence equation, interpolation for insufficiently smooth functions and the computation of singular integrals. These experiments are all starting from the simplest cases and draw new conclusions through observation, comparison, analysis and conjecture, which are helpful to train the students’ innovative thinking ability, as well as provide better guidance for the practical teaching in numerical analysis.

Key words:numerical analysis; fitting for recurrence equation; interpolation for insufficiently smooth function; computation of singular integral; Mathematica software

[收稿日期]2015-09-05；[修改日期] 2016-03-26

[基金项目]天津市普通高等学校本科教学质量与教学改革研究计划项目

[作者简介]王同科(1965-),男,博士,教授,从事计算数学研究.Email:wangtke@sina.com

[中图分类号]O241

[文献标识码]C

[文章编号]1672-1454(2016)02-0057-07