基于穴度的三维时空优化问题的贪心调度算法*

朱　鹏，何　琨，曹伟刚，杨　欢华中科技大学 计算机科学与技术学院，武汉 430074

基于穴度的三维时空优化问题的贪心调度算法*

朱鹏，何琨+，曹伟刚，杨欢
华中科技大学 计算机科学与技术学院，武汉 430074

ZHU Peng,HE Kun,CAO Weigang,et al.Caving-degree based greedy scheduling algorithm for threedimensional space-time optimization problem.Journal of Frontiers of Computer Science and Technology, 2016,10(8)：1051-1062.

摘要：研究了基于二维矩形Packing的三维时空优化问题，即对给定的一个任意宽、高的大矩形框和有限个有连续加工时间要求的任意宽、高的小矩形块，如何安排每个小矩形块的入框时刻及其出框前每一时刻的位置和方向，使得所有小矩形块的总加工时间即总调度长度makespan最短。与经典布局问题的不同之处在于，各矩形块在框内可随时间的绵延而改变其位置和方向，从而能更充分地利用矩形框的空间。基于实角与实占角动作的定义，设计了求解其子问题二维矩形Packing问题的增强穴度算法。然后，每步迭代优先考虑剩余加工时间长的矩形块，提出了求解此问题的贪心穴度调度算法（caving-degree based greedy scheduling algorithm，CGSA）。作为比较，同时设计了矩形块在框内不可随时间移动的将时间简单类比为空间的对应Packing问题的调度算法 CGSA′。对于实验中提出的满足非闸断模式的4个小型算例，它们在原问题上的最优调度长度为2，但若将时间简单地类比为空间，即矩形块放入框内后不可随时间移动其方位，则其最优调度长度为3。实验表明，算法CGSA在这4个非闸断算例上均得到了最优调度。进一步地研究出满足闸断模式的21组共210个自动生成算例，通过实验验证了算法CGSA的最优解的数目明显多于CGSA′，且CGSA的平均调度长度明显短于CGSA′。

关键词：时空优化；贪心调度；装箱；算例；布局

1　引言

本文研究以二维矩形Packing问题为子问题，进一步考虑时间因素的三维时空优化问题。此类考虑时间与空间的复合优化问题，在现实生活中有着广泛的应用，例如内存空间的分配、处理机的调度[1-2]、数据库存储空间的分配、饼干的烘制、组装线的调度[3]等。以内存空间的分配为例，将待分配的内存空间视为一个大的矩形框，将待调度的作业视为形状大小给定的小矩形块，将作业需要连续调度的时间区间长度视为矩形块需要持续放入矩形框内的时间长度。如图1所示，从而可将如何调度这些作业使其占用内存空间的时间跨度最短的问题转化为如何调度和布局这些小矩形块使大矩形框被占用的时间跨度最短的装箱调度问题。

Fig.1　Memory scheduling schematic图1　内存调度示意图

黄文奇、何琨于2010年提出了考虑时间因素的三维装箱工作的优化调度问题[4]，并给出了其可计算性的完整证明[5-6]。到目前为止，国内外文献中尚未见到其快速求解算法和相关算例的研究。

对于其二维退化情形即三维时空优化问题，其子问题二维矩形Packing问题已被证明是强NP难度问题[7]。在此基础上，三维时空优化问题还需考虑连续量时间的变化，因此其计算复杂度非常高。目前国内外文献中尚未见到相关快速求解算法和算例的研究。

对于其子问题即二维矩形Packing问题，自20世纪60年代以来，国内外学者做了大量的研究。目前，具有代表性的算法可以分为随机型算法和确定型算法两大类。其中随机型算法主要包括遗传算法[8-10]、模拟退火算法[11]、粒子群算法[12]、蚁群算法[13]等；确定型算法主要包括BL（bottom left）算法[14]、BLF（bottom left fill）算法[15]、BLD（bottom left decreasing）算法[16]、分支限界法[17]、拟物拟人法[18-21]等。

本文拟对三维时空优化问题的快速求解算法进行研究。首先对于其子问题——二维矩形Packing问题，在基于动作空间的穴度算法[22]的基础上，提出了基线与实角的概念，以提高算法的计算速度。然后，优先考虑剩余加工时间长的矩形块，设计了求解三维时空优化问题的贪心算法。并进一步设计了结合问题特色和优势的若干小型算例和自动生成算例，以检测算法的性能。

2　问题描述

三维时空优化问题是指在二维欧氏空间中，已知一个宽W、高H分别任意给定的大矩形框和n个宽Wi、高Hi分别任意给定的需要连续加工的小矩形块，各矩形块的待加工时间Ti也任意给定。其中n为任意给定的正整数，其他参数均为正有理数。问如何在矩形框内安排所有的小矩形块，使最后取出的那个矩形块的出框时刻最小。即要求给出：

（1）每个矩形块放入容器的时刻Si；

（2）每个矩形块在时间区间[Si,Si+Ti)内的每一时刻所处的位置和方向。

目标是使得所有小矩形块的总加工时间即总调度长度makespan最小，即使得公式 max(S1+T1,S2+ T2,…,Sn+Tn)－min(S1,S2,…,Sn)最小。

约束条件为任意时刻放入的矩形块完全在框内，边平行于大矩形框的边，且各小矩形块之间两两互不嵌入。

此问题虽然与二维欧氏空间中的Packing问题有关，但不是二维矩形Packing问题，也不是三维欧氏空间中的Packing问题，而是要随着时间的改变在二维欧氏空间中规划诸矩形块在矩形框中的存放和运动。

若将此问题中的时间物理量简单地类比为空间物理量，则此问题退化为高方向固定的三维Strip Packing问题[23]。三维Strip Packing问题是指给定一个底面长宽固定、高无限的长方体箱，如何将给定的有限个小长方体无嵌入地、正交地放入到长方体箱中，使得放入后小长方体的最高高度最小。若小长方体的高不可旋转，则为高方向固定的Strip Packing问题。若将小矩形块的加工时间视为小长方体的高，则矩形框的总体利用时间相当于长方体箱的最高高度，退化后两个问题等价。

在三维时空优化问题中，小矩形块在大矩形框中每一时刻均可改变其位置和方向进行再调度，因此该问题的最优解一定不劣于高方向固定的三维Strip Packing问题的最优解。

3　算法描述

在调度过程中，如果每一时刻均能保证矩形框空间的利用率为100%，那么所得调度的makespan必然最短。因此首先需要设计矩形Packing问题的高效求解算法，使得每一时刻矩形框尽量布满。首先给出基于实角的矩形Packing问题的增强穴度算法。在此基础上，进一步设计了三维时空优化问题的贪心穴度调度算法。

3.1矩形Packing问题的增强穴度算法

对于子问题二维矩形Packing问题，本文参考基于动作空间的穴度算法，定义了基线、实角和虚角等概念，并改进了穴度的内容，提出了基于实角的二维矩形Packing问题的增强穴度算法，包括基本穴度算法A0与增强穴度算法A1。

3.1.1相关概念的定义

定义1（格局）设某个时刻，矩形框内已经放入了若干个矩形块，还有若干个矩形块待放，这称为一个格局。格局可分为初始格局、当前格局和终止格局。框内未放入任何块时为初始格局。框内已经放满或者容器外剩余的矩形块无法再放入时为终止格局。对每一格局，可用布局X＝(x1,y1,o1,x2,y2,o2,…, xn,yn,on)来描述小矩形块在大矩形框中的位置和方向。其中xi、yi表示块i的左下角坐标，oi表示块i的放入方向为横放还是竖放。

定义2（基线）基线是指在当前格局下，所有已经放入的小矩形块的边以及大矩形框的边。

初始格局只有4条基线，即大矩形框的4条边。基线是一种描述边界的方法，又细分为垂直基线和水平基线。

定义3（动作空间）在当前格局下，往矩形框中合法地放入一个虚拟的矩形块。若该矩形块的上、下、左、右均与已放入矩形块的边或框边相贴（即重合的长度大于0），则该虚拟的矩形块所占的空间称为当前格局下的一个动作空间。

如图2所示，矩形块BCDQ和ABPF为动作空间。动作空间由4条基线或其延长线所围成。

Fig.2　An example of action space and angle图2　动作空间与角示例

定义4（实角与虚角）动作空间的每一个角由一个顶点和两条基线或其延长线所围成。又分为实角和虚角。实角由两条基线所围成，虚角的两条边中至少有一条是基线的延长线。

如图2所示，在动作空间BCDQ中，角QBC、BCD、CDQ是实角，角BQD是虚角。

定义5（实占角动作）在当前的格局下，若将一个矩形块放入到动作空间的一个实角，使放入块的顶点和角的顶点重合，顶点对应的边分别与角的两条边相贴，而且该放入块不超出动作空间，则称此动作为一个实占角动作。

对于每个小矩形块的放入，不是单纯地考察当前矩形框的面积利用率，而是尽量希望能从整体层面来进行评价。直观地来讲，如果小矩形块放入后，剩余空间参差不齐，则不利于后续块的放入；如果放入后，剩余空间比较平整，那么对后续的放置就留下了较大的余地。

定义6（重合度co）重合度是指放入矩形块与已放入矩形块以及大矩形框相贴的边长与矩形块的周长之比。

定义7（相近度ed）相近度与最小距离dmin有关，记为ed=exp(-dmin)，最小距离是指放入矩形块与所有未相贴的已放入矩形块之间的最小距离。

定义8（穴度）穴度是一个三元组，为 。其中，k表示贴边数，即放入矩形块与当前动作空间相贴的边的数目；co表示重合度；ed表示相近度。

穴度表示实占角动作与当前动作空间的紧密程度，穴度的比较即依字典序比较此三元组的大小。穴度越大，说明放入块与动作空间相贴的边越多，与其他放入块或框相贴的比率越大，与其他放入块距离越近，从而与实动作空间的吻合程度越好。

定义9（评判准则）受到围棋里面“金角银边草肚皮”思想的启发，在进行实占角动作选取时，对每个实占角动作，采取以下评判标准。

（1）穴度：大优先；

（2）放入块的面积：大优先；

（3）块的长边长：大优先；

（4）块左下顶点的x坐标：小优先；

（5）块左下顶点的y坐标：小优先；

（6）块的方向：躺优先。

按照上述评判准则，可唯一地确定一个好的实占角动作。

3.1.2基本穴度算法

基于以上定义，设计A0算法作为二维矩形Packing的基本穴度算法。基本穴度算法描述如下。

算法1基本穴度算法A0

输入：大矩形框的宽和高；每个小矩形块的宽和高。

输出：布局以及面积利用率。

1.初始化动作空间以及实角，初始化实占角动作

2.While存在实占角动作do

3.根据评判准则，选择最优的实占角动作

4.If大矩形框被小矩形框完全填充

5.保存布局，退出

6.Else

7.更新动作空间以及实角

8.更新实占角动作

9.End while

10.输出布局以及面积利用率

3.1.3增强穴度算法

A0属于贪心算法，在当前最优的情况下不一定保证总体上达到最优。这里对基本穴度算法进行改进，加入搜索过程以提升解的质量。增强穴度算法A1是指从初始格局出发，每一步考查穴度最大的前N个实占角动作，然后通过向前看并回溯的方法最终选择一个实占角动作。

对于N值的设定，遵循下列规则：

N=[当前格局下所有实占角动作的数目×k%]

若N lowerbound，则N=upperbound。

为避免搜索的范围过小，对N的取值设定了一个下界；考虑到计算时间，只选择穴度较大的固定数量的动作进行回溯。

增强穴度算法描述如下：

算法2增强穴度算法A1

输入：大矩形框的宽和高；每个小矩形块的宽和高。

输出：布局以及面积利用率。

1.初始化动作空间，初始化实角，初始化实占角动作

2.While存在实占角动作do

3.实占角动作排序，选择前N个最优的实占角动作

4.对前N个实占角动作的每一个动作执行A0至终止格局，选择面积利用率最大的实占角动作来做

5.更新动作空间

6.End while

7.输出布局以及面积利用率

3.2贪心穴度调度算法

3.2.1基本思想和相关概念的定义

在求解子问题矩形Packing问题的增强穴度算法的基础上设计求解原问题的贪心穴度调度算法。此算法每一步基于某种贪心策略，在选择当前候选放入块子集时，优先考虑剩余加工时间较长的矩形块，再利用算法A1对该子集安排尽可能多的矩形块到框内进行加工，直至某个时刻有至少一个块加工完成；取出加工完成的块，在保证未加工完成的块仍在框内的前提下，重新选择候选块子集，并继续安排放入尽可能多的矩形块到框内加工，如此反复，直至所有块加工完成。每一步安排放入块至框内的过程称为一次调度。

定义10（加工区间）一次调度完成后，从t1时刻开始对安排放入的小矩形块进行加工，直至某一时刻t2有至少一个矩形块加工完毕，其对应的时间段[t1,t2)称为一个加工区间。

定义11（剩余加工时间）当前时刻某矩形块尚需的持续加工时间长度称为其剩余加工时间，块在未加工前，其剩余加工时间等于该块的待加工时间。

下面给出两种平均剩余加工时间tavg的定义，每一种定义对应一种策略。

定义12（平均剩余加工时间tavg1）考虑当前时刻剩余加工时间大于0的矩形块集合，设tmax、tmin为该集合中最大、最小剩余加工时间，平均剩余加工时间tavg1定义为tavg1=(tmax+tmin)/2。

定义13（平均剩余加工时间tavg2）仅考虑当前时刻尚未开始加工的框外的矩形块集合，其平均剩余加工时间tavg2定义为该集合剩余加工时间的平均值。

3.2.2贪心穴度调度算法

三维时空优化问题的调度算法是在二维矩形Packing求解算法的基础上，进行多次调度与加工，直至所有矩形块加工完毕。

调度时可以考虑时间上的贪心，即优先考虑剩余加工时间较长的矩形块。因为如果加工时间长的矩形块放到了最后执行，则易导致最后的空间有较多的浪费，从而导致时间消耗的上升。但如果仅优先考虑剩余加工时间长的矩形块，可能会导致调度后矩形框的空间利用率不是很理想，最终也会导致时间消耗上升。因此，调度算法需要综合考虑时间与空间。基于上述考虑，设计了贪心穴度调度算法（caving-degree based greedy scheduling algorithm，CGSA），该算法有两种调度类型，分别称为常规调度和修正调度。

令LF为所有剩余加工时间大于0的矩形块集合，令V1为集合LF中剩余加工时间大于等于平均剩余加工时间tavg的矩形块集合，令V2为集合LF中前一加工区间内未加工完成的矩形块集合，令集合V=V1∪V2。

常规调度使用算法A1，在实占角动作的选取上，对每个实占角动作，优先考虑集合V1中的矩形块，否则依据评判准则（定义9）选择块及放入方位。常规调度有可能会出现集合V2中的矩形块不在框内的情况，这时不满足块需要连续加工的要求，称为一次异常调度。此时需要进行修正调度。

修正调度有两个处理步骤：

步骤1忽略异常调度的布局，使用算法A1，在实占角动作的选取上，对每个实占角动作，优先考虑集合V中的矩形块，否则依据评判准则（定义9）选择块及放入方位。

步骤2若步骤1仍出现异常调度，则忽略该异常调度的结果，将集合V2中的矩形块紧凑平移到框的左下角。平移后，更新动作空间，然后在框的未填充区域进行常规调度。

贪心穴度调度算法CGSA描述如下：

算法3贪心穴度调度算法CGSA

输入：大矩形框的宽、高；每个小矩形块的宽、高与待加工时间。

输出：每次加工区间内的布局与总调度长度。

1.初始化所有小矩形块的剩余加工时间

2.While矩形框外有未加工完的矩形块do

3.进行常规调度

4.If出现异常调度

5.进行修正调度

6.保留加工区间内的布局，对框内小矩形块进行加工

7.更新未加工完的小矩形块的剩余加工时间

8.End while

9.输出每个加工区间内的布局及总调度长度

常规调度综合考虑了时间与空间的因素。若在常规调度后，集合V2中的矩形块没有完全在框内，则进行修正调度。

修正调度只在常规调度出现异常时使用，其步骤1也综合考虑了时间与空间的因素，如果步骤1调度不是异常调度，则不执行步骤2。修正调度步骤1与常规调度的唯一区别是在实占角动作的选取上优先考虑集合V，调度后集合V2中的块都在框内的几率会大于常规调度，但是框的利用率也许没有常规调度的理想。修正调度的步骤1仍然有可能出现异常调度，比如调度后未将集合V中所有矩形块放入框中，而集合V中未放入框内的块恰好有至少一个属于集合V2。此时需要执行步骤2。步骤2没有将集合V2中的块拿到框外，可以确保调度的合理性。

作为比较，设计了矩形块在框内不可随时间移动的将时间简单类比为空间的相应问题的调度算法CGSA′。具体过程如下。

算法4贪心穴度调度算法CGSA′

输入：大矩形框的宽、高；每个小矩形块的宽、高与待加工时间。

输出：每次加工区间内的布局与总调度长度。

1.初始化所有小矩形块的剩余加工时间

2.While矩形框外有未加工完的矩形块do

3.在框的未填充区域进行常规调度

4.保持加工区间内的布局，对框内小矩形块进行加工

5.取出框内加工完成的块。保留框内未加工完成的块的放置方位，更新其剩余加工时间

6.更新动作空间

7.End while

8.输出每个加工区间内的布局及总调度长度

4　算例设计与运行结果

将贪心穴度调度算法用C++语言编程，并在CPU主频为2.80 GHz，内存为4 GB的微型计算机上进行计算。对于矩形Packing问题，国际上有公开的代表性算例进行校验。然而，三维时空优化问题，是近年来学术界提出的新问题，目前国际上还没有公开的算例。因此，如何设计出公平公正并具代表性的算例，是本文首先需要解决的问题。本文共有两大类算例：第一大类为满足非闸断模式的小型算例；第二大类为满足闸断模式的自动生成算例。然后对这两大类算例进行实验计算和结果分析。

4.1小型算例及其运行结果

本节设计了4个小型算例，它们的理论最优解即最优调度长度均为2，但如果退化为相应的Strip Packing问题，其理论最优调度长度均为3。表1到表4分别描述了这4个算例中小矩形块的相应参数，其中Ri代表小矩形块，Wi、Hi分别代表小矩形块的宽、高，Ti代表小矩形块的待加工时间。

Table 1　Small scale case 1(the shape of rectangle:10×10)表1　小型算例1（框的形状为10×10）

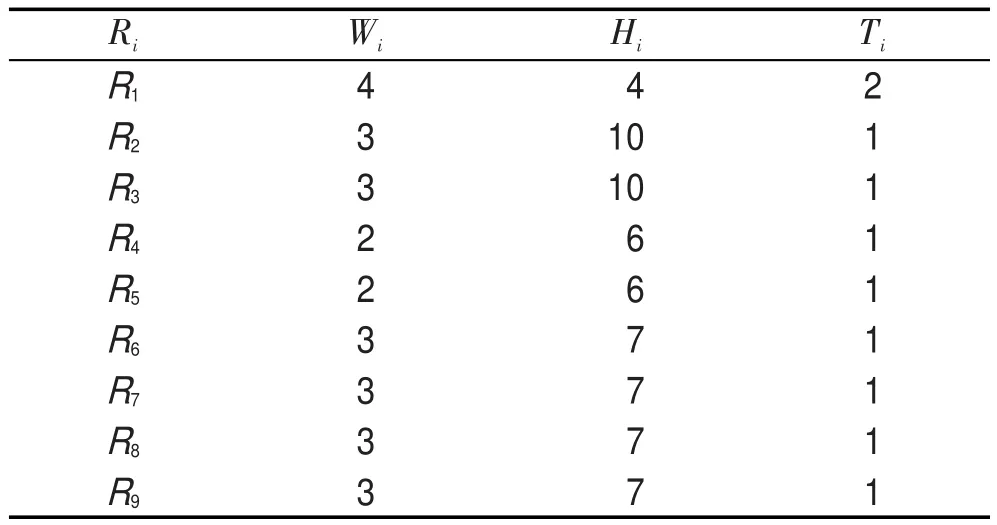
Table 2　Small scale case 2(the shape of rectangle:10×10) 表2　小型算例2（框的形状为10×10）

Table 3　Small scale case 3(the shape of rectangle:5×5) 表3　小型算例3（框的形状为5×5）

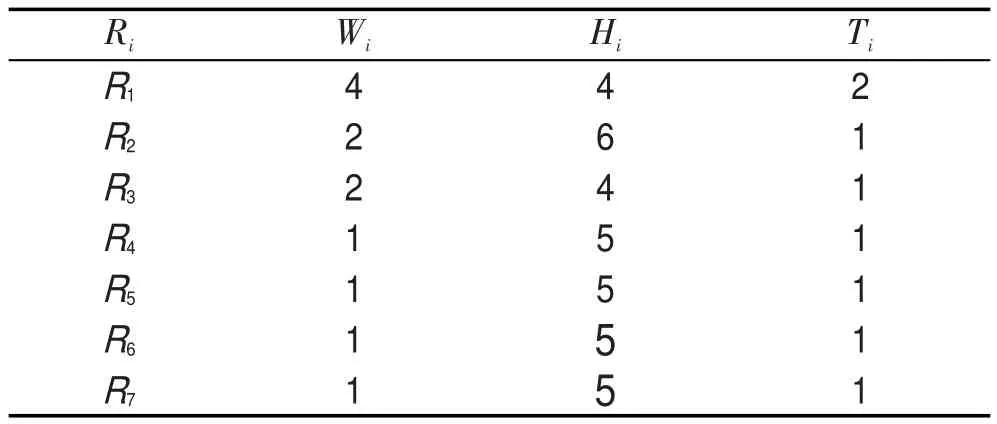
Table 4　Small scale case 4(the shape of rectangle:6×6) 表4　小型算例4（框的形状为6×6）

当取tavg=tavg1时，算法CGSA对这4个算例均计算出了总调度长度为2的最优解，而算法CGSA′得到的总调度长度都为3。表5给出了小型算例2在不同加工区间内的布局。

Table 5　Coordinates of packing layouts for small scale case 2表5　小型算例2的布局坐标

在用算法CGSA测试时，每个算例的每个加工区间内大矩形框的面积利用率都是100%。图3～图6分别给出了这4个测试算例在每个加工区间内的布局图。图中阴影部分为矩形块在不同加工区间内持续加工的位置与方向。

Fig.3　Packing layouts for small scale case 1图3　小型算例1的布局图案

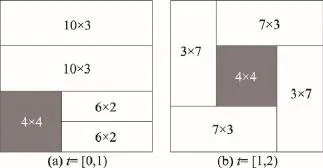
Fig.4　Packing layouts for small scale case 2图4　小型算例2的布局图案

Fig.5　Packing layouts for small scale case 3图5　小型算例3的布局图案

Fig.6　Packing layouts for small scale case 4图6　小型算例4的布局图案

4.2自动生成算例及其运行结果

由小型算例的布局图可知，4个算例在每个单位长度的加工区间内都保证了空间利用率为100%，最终的布局图的数目表明它们均达到了总调度长度为2的最优解。由此启发在设计自动生成算例时，可针对每个加工区间自动生成放入块的尺寸，若在连续i个加工区间都包含某个相同尺寸的矩形块，则可将其视为同一个矩形块，并将此矩形块需要连续加工的时间设为这i个加工区间长度之和。

以小型算例4为例，如图6所示，两个单位长度的加工区间布局图表明总调度长度是两个单位时间。矩形块4×4在两个加工区间中均有出现，则将其视为一个矩形块且其连续加工时间为2，其余块的加工时间设为1。

根据上述分析，设计算例的自动生成算法。首先将每个加工区间进行单独分割，然后合并相邻加工区间中尺寸相同的矩形块，并计算合并后不同矩形块的待加工时间。

在分割过程中，可能会出现某一层分割后的尺寸很大（接近矩形框的尺寸大小），而某一层分割后的矩形块大部分尺寸都是单位矩形块（尺寸为1×1），这样的算例对于问题的研究没有意义。为了使生成后的算例更具代表性，设定需要生成的小矩形块的数目nl=(W+H)/2×(L±1)，设定每个加工区间内需要切割的矩形块的数目n0=nl/L×(1±0.2)，其中W、H为大矩形框的宽、高，L为需要分割的加工区间个数，nl与n有关，将分割后nl个小矩形块中具有相邻加工区间且尺寸相同的块进行合并，得到的值为给定的小矩形块的数目n。

算例自动生成算法如下。

算法5算例自动生成算法

输入：大矩形框的宽和高，需要分割的加工区间个数，需要生成的小矩形块数目。

输出:小矩形块的宽和高以及待加工时间。

1.For每个加工区间do

2.随机生成需要分割的小矩形块的数目

3.While小矩形块数目少于需要分割的数目do

4.随机选择一个该加工区间已有的矩形块

5.调用矩形块分割算法将随机选择的矩形块进行分割

6.储存分割后生成的小矩形块

7.End while

8.End for

9.将相邻加工区间中尺寸相同的矩形块视为一个块，合并其加工时间

10．将所有小矩形块的顺序随机排列

算法5中调用了矩形块分割算法，把一个矩形块随机分割成两个小的矩形块，且两个小矩形块的边长为整数。矩形块分割算法描述如下，其中random (U)指从U集合中随机选择一个元素输出。

算法6矩形块分割算法

输入：待分割矩形块的宽和高w、h。

输出:分割后两个小矩形块的宽和高(w1,h1)、(w2,h2)。

1.初始化：w1←w,w2←w,h1←h,h2←h

2.随机选择分割宽或高

3.If分割宽

4.w1←random({1,2,…,w-1})

5.w2←w-w1

6.If分割高

7.h1←random({1,2,…,h-1})

8.h2←h-h1

9.输出(w1,h1)、(w2,h2)

用算法5生成了G21算例集，该算例集共有21种类型算例，且每种类型有10个算例。依据最优调度长度的不同，将G21算例集分为7组，分别为Gi(i=1,2,3,4,5,6,7)，每组算例内的最优调度长度相同，分别为i+1(i=1,2,3,4,5,6,7)个单位时间，例如G3算例组中所有算例的最优调度长度为3+1=4个单位时间。在统计算例的运行结果时，以算例组为单位。

每组算例包含3种类型，分别为Gi_10、Gi_12、Gi_15，如G2_12表示G2算例组中的第2类算例，该类算例共有10个。表6给出了Gi算例组的特征。

Table 6　Features ofGigroup表6　Gi算例组的特征

G21算例集中的每个矩形块都有其对应的待加工时间，表7统计了每种类型算例在不同待加工时间中拥有矩形块的平均数目。平均数目是取每种类型算例中10个算例的平均值。

对于算法CGSA，其平均剩余加工时间tavg可以选取tavg1、tavg2，分别对应两种贪心策略。图7描述了算法CGSA在G21算例集上不同贪心策略下求得的平均调度长度。平均调度长度是取每个算例组中30个算例求得的总调度长度的平均值。

由结果可知，在测试G21算例集上，算法GCSA 取tavg=tavg1时得到的结果明显优于取tavg=tavg2时的结果，且在运行时间上前者明显比后者运行时间短。在接下来的测试中，算法CGSA与CGSA′都取tavg=tavg1。

算法CGSA在测试G21算例集时，使用修正调度的概率很低，执行修正调度步骤2的概率更低，且如果每次调度都用修正调度，算法得到的总调度长度和运行时间都远高于使用常规调度的情况。

Table 7　Average number of rectangles表7　矩形块的平均数目统计

Fig.7　Average scheduling length in different greedy strategies for CGSA图7CGSA在不同贪心策略下的平均调度长度

分别用算法CGSA与CGSA′对G21算例集进行测试，图8描述了算法CGSA与CGSA′在Gi算例组中达到最优解的算例数。

Fig.8　Number of optimal solutions inGigroup图8　Gi算例组中达到最优解的算例数

图9描述了算法CGSA与CGSA′在算例组Gi中所得的平均调度长度。

Fig.9　Average scheduling length for CGSAand CGSA′图9CGSA与CGSA′的平均调度长度

4.3运行结果分析

对于设计的4个小型算例，贪心穴度调度算法CGSA在测试时均得到了总调度长度为2的最优解。若将时间简单地类比为空间，则问题退化为高方向固定的Strip Packing问题，其最优调度长度为3；若限定矩形块在放入矩形框的时间段内不能移动，则贪心调度的总调度长度也为3。对于自动生成的G21算例集，算法CGSA在测试时均能获得半数及半数以上的最优解。当最优调度长度分别为2、3、4时，相应算例组中很多算例都能达到最优解。当最优调度长度由5增加到8，相应算例组中达到最优解的算例数目逐渐减少。对比算法CGSA与CGSA′的测试结果可知，矩形块在放入矩形框的时间段内可以移动的情况下，贪心调度在每个算例组中得到最优解的算例数明显多于矩形块在放入矩形框的时间段内不能移动的情况，且前者得到的总调度长度也短于后者。由此表明，将时间特殊处理时，加强了时空利用的灵活性，提高了矩形框的时间空间利用率。

5　结束语

本文对三维时空优化问题的算例和近似求解算法进行了研究，提出了优先考虑矩形块的剩余加工时间的贪心穴度调度算法CGSA。设计了基于问题特点与优势的满足非闸断模式和闸断模式的两类算例。实验结果表明，算法CGSA在非闸断模式算例上均得到了最优调度，在多数非闸断模式的算例上得到了最优调度。在今后的研究中，将生成更高复杂度的代表性算例，进一步改进算法以提高其计算优度和效率。

References:

[1]Coffman E G Jr,Garey M R,Johnson D S.An application of bin-packing to multiprocessor scheduling[J].SIAM Journal on Computing,1978,7(1):1-17.

[2]Chekuri C,Khanna S.On multi-dimensional packing problems[C]//Proceedings of the 10th ACM-SIAM Symposium on Discrete Algorithms,Baltimore,USA,Jan 17-19,1999. Philadelphia,USA:SIAM,1999:185-194.

[3]Wee T S,Magazine M J.Assembly line balancing as generalized bin-packing[J].Operational Research Letters,1982, 1:56-58.

[4]Huang Wenqi,He Kun.Optimal time scheduling on the three-dimensional space packing[J].Journal of Huazhong University of Science and Technology:Natural Science Edition,2010,38(12):102-104.

[5]Huang Wenqi,He Kun.An optimal time scheduling problem on cuboids packing over four-dimensional space-time and its computability proof[J].Chinese Journal of Computer, 2013,36(9):1880-1888.

[6]Huang Wenqi,He Kun.On the weak computability of a four dimensional orthogonal packing and time scheduling problem[J].Theoretical Computer Science,2013,501:1-10.

[7]Michael R G,David S J.Computers and intractability:a guide to the theory of NP-completeness[M].San Francisco, USA:WH Freeman&Co,1979.

[8]Hopper E,Turton B.A genetic algorithm for a 2D industrial packing problem[J].Computers&Industrial Engineering, 1999,37(1):375-378.

[9]Kröger B.Guillotineable bin packing:a genetic approach[J]. European Journal of Operational Research,1995,84(3): 645-661.

[10]Bortfeldt A.A genetic algorithm for the two-dimensional strip packing problem with rectangular pieces[J].European Journal of Operational Research,2006,172(3):814-837.

[11]Leung T W,Chan C K,Troutt M D.Application of a mixed simulated annealing-genetic algorithm heuristic for the twodimensional orthogonal packing problem[J].European Journal of Operational Research,2003,145(3):530-542.

[12]Jiang Jiaqian,Liang Youcheng.A hybrid algorithm based on PSO and SA and its application for two-dimensional non-guillotine cutting stock problem[C]//LNCS 3037:Proceedings of the 4th International Conference on Computational Science,Kraków,Poland,Jun 6-9,2004.Berlin,Heidelberg:Springer,2004:666-669.

[13]Dorigo M,Blum C.Ant colony optimization theory:a survey [J].Theoretical Computer Science,2005,344(2):243-278.

[14]Baker B S,Coffman E G Jr,Rivest R L.Orthogonal packings in two dimensions[J].SIAM Journal on Computing,1980,9 (4):846-855.

[15]Chazelle B.The bottomn-left bin-packing heuristic:an efficient implementation[J].IEEE Transactions on Computers, 1983,100(8):697-707.

[16]H opper E.Two-dimensional packing utilising evolutionary algorithms and other meta-heuristic methods[D].Cardiff: University of Wales,2000.

[17]Cui Yaodong,Yang Yuli,Cheng Xian,et al.A recursive branch-and-bound algorithm for the rectangular guillotine strip packing problem[J].Computers&Operations Research, 2008,35(4):1281-1291.

[18]Huang Wenqi,Liu Jingfa.A deterministic heuristic algorithm based on Euclidian distance for solving the rectangles packing problem[J].Chinese Journal of Computer,2006,29 (5):734-739.

[19]Wu Yuliang,Huang Wenqi,Lau S,et al.An effective quasihuman based heuristic for solving the rectangle packing problem[J].European Journal of Operational Research, 2002,141(2):341-358.

[20]Huang Wenqi,Chen Duanbing,Xu Ruchu.A new heuristic algorithm for rectangle packing[J].Computers&Operations Research,2007,34(11):3270-3280.

[21]Huang Wenqi,Chen Duanbing.An efficient heuristic algorithm for rectangle-packing problem[J].Simulation Modelling Practice and Theory,2007,15(10):1356-1365.

[22]He Kun,Huang Wenqi,Jin Yan.Efficient algorithm based on action space for solving the 2D rectangular packing problem[J].Journal of Software,2012,23(5):1037-1044.

[23]Allen S D,Burke E K,Kendall G.A hybrid placement strategy for the three-dimensional strip packing problem[J].European Journal of Operational Research,2011,209(3):219-227.

附中文参考文献：

[4]黄文奇,何琨.三维装箱工作的优化调度问题[J].华中科技大学学报:自然科学版,2010,38(12):102-104.

[5]黄文奇,何琨.四维时空高效利用的装箱调度问题及其可计算性证明[J].计算机学报,2013,36(9):1880-1888.

[18]黄文奇,刘景发.基于欧氏距离的矩形Packing问题的确定性启发式求解算法[J].计算机学报,2006,29(5):734-739.

[22]何琨,黄文奇,金燕.基于动作空间求解二维矩形Packing问题的高效算法[J].软件学报,2012,23(5):1037-1044.

ZHU Peng was born in 1990.He received the M.S.degree in computer science and technology from Huazhong University of Science and Technology in 2015.His research interests include algorithm design and combinatorial optimization,etc.

朱鹏（1990—），男，2015年于华中科技大学计算机科学与技术专业获得硕士学位，主要研究领域为算法设计与分析，组合优化等。

HE Kun was born in 1972.She is an associate professor and Ph.D.supervisor at School of Computer Science and Technology,Huazhong University of Science and Technology.Her research interests include algorithm design, combinatorial optimization and data mining,etc.

何琨（1972—），女，华中科技大学计算机科学与技术学院副教授、博士生导师，主要研究领域为算法设计与分析，组合优化，数据挖掘等。

CAO Weigang was born in 1987.He is an M.S.candidate at School of Computer Science and Technology,Huazhong University of Science and Technology.His research interests include algorithm design and combinatorial optimization，etc.

曹伟刚（1987—），男，华中科技大学计算机科学与技术学院硕士研究生，主要研究领域为算法设计与分析，组合优化等。

YANG Huan was born in 1992.She is an M.S.candidate at School of Computer Science and Technology,Huazhong University of Science and Technology.Her research interests include algorithm design and combinatorial optimization,etc.

杨欢（1992—），女，华中科技大学计算机科学与技术学院硕士研究生，主要研究领域为算法设计与分析，组合优化等。

*The National Natural Science Foundation of China under Grant Nos.61472147,61173180(国家自然科学基金). Received 2015-07,Accepted 2015-11.

CNKI网络优先出版:2015-11-12,http://www.cnki.net/kcms/detail/11.5602.TP.20151112.1658.010.html

文献标志码：A

中图分类号：TP301

doi:10.3778/j.issn.1673-9418.1507045

Caving-Degree Based Greedy SchedulingAlgorithm for Three-Dimensional Space-Time Optimization Problemƽ

ZHU Peng,HE Kun+,CAO Weigang,YANG Huan
School of Computer Science and Technology,Huazhong University of Science and Technology,Wuhan 430074,China +Corresponding author:E-mail:brooklet60@gmail.com

Abstract:This paper addresses the three-dimensional space-time optimization(3D-STO)problem based on twodimensional rectangular packing problem.Given a large rectangular sheet and a set of rectangular items,each item needs to be continuously processed with a time length on the sheet.The question is how to arrange each itemƳs loading time and its location and orientation during the processing period,and the goal is to minimize the total utilization time of the sheet,i.e.the makespan of the schedule.Differing from classical packing problems,each itemƳs location and orientation on the sheet can be changed over time such that the sheet is utilized more fully.Based on the definitions of real corner and real corner action,this paper designs an enhanced caving-degree algorithm for the sub-problem,the twodimensional rectangular packing problem.Then by assigning a higher priority to items with longer remaining processing time at each step,this paper proposes a caving-degree based greedy scheduling algorithm(CGSA)for the 3D-STO. For comparison,this paper also proposes a scheduling algorithm called CGSA′in which each itemƳs location and orientation on the sheet canƳt be changed over time.Four small benchmarks with no guillotine cut constraint presented in the experiments,CGSA achieves optimal solutions whose makespan is 2.But if the experiments regard the time as a space dimension,indicating that the items canƳt move over time,the shortest makespan is 3.Further,this paper gener-ates 21 groups with a total of 210 guillotine cut constraint benchmarks.Experiments show that CGSA not only achieves more optimal solutions than CGSA′,but also obtains shorter average scheduling length than CGSA′.

Key words:space-time optimization;greedy scheduling;packing;benchmarks;placement