Numerical solution of thermo-solutal mixed convective slip flow from a radiative plate with convective boundary condition*
M. J. UDDIN, O. Anwar BÉG, M. N. UDDIN, A. I. Md. ISMAIL
1. Department of Mathematics, American International University-Bangladesh, Dhaka, Bangladesh,
E-mail:jashim_74@yahoo.com
2. Fluid Mechanics, Spray Research Group, Petroleum and Gas Engineering Division, Room G77, Newton Building, School of Computing, Science and Engineering (CSE), University of Salford, M54WT, UK
3. Department of Mathematical Sciences, Ball State University, 2000 W University Avenue, Muncie, IN 47306,USA
4. School of Mathematical Sciences, Universiti Sains Malaysia, Penang 11800, Malaysia
Numerical solution of thermo-solutal mixed convective slip flow from a radiative plate with convective boundary condition*
M. J. UDDIN1*, O. Anwar BÉG2, M. N. UDDIN3, A. I. Md. ISMAIL4
1. Department of Mathematics, American International University-Bangladesh, Dhaka, Bangladesh,
E-mail:jashim_74@yahoo.com
2. Fluid Mechanics, Spray Research Group, Petroleum and Gas Engineering Division, Room G77, Newton Building, School of Computing, Science and Engineering (CSE), University of Salford, M54WT, UK
3. Department of Mathematical Sciences, Ball State University, 2000 W University Avenue, Muncie, IN 47306,USA
4. School of Mathematical Sciences, Universiti Sains Malaysia, Penang 11800, Malaysia
A mathematical model for mixed convective slip flow with heat and mass transfer in the presence of thermal radiation is presented. A convective boundary condition is included and slip is simulated via the hydrodynamic slip parameter. Heat generation and absorption effects are also incorporated. The Rosseland diffusion flux model is employed. The governing partial differential conservation equations are reduced to a system of coupled, ordinary differential equations via Lie group theory method. The resulting coupled equations are solved using shooting method. The influences of the emerging parameters on dimensionless velocity, temperature and concentration distributions are investigated. Increasing radiative-conductive parameter accelerates the boundary layer flow and increases temperature whereas it depresses concentration. An elevation in convection-conduction parameter also accelerates the flow and temperatures whereas it reduces concentrations. Velocity near the wall is considerably boosted with increasing momentum slip parameter although both temperature and concentration boundary layer thicknesses are decreased. The presence of a heat source is found to increase momentum and thermal boundary layer thicknesses but reduces concentration boundary layer thickness. Excellent correlation of the numerical solutions with previous non-slip studies is demonstrated. The current study has applications in bioreactor diffusion flows and high-temperature chemical materials processing systems.
slip flow, thermal radiation, lie group theory, heat source/sink, materials processing
Introduction
Slip flows occurs in a diverse range of technological applications including sheet processing[1], nuclear power systems[2], and foam production[3]and fluidic cells in medicine[4]. Slip flows require a modification of the classical “no-slip” velocity boundary condition at a wall with a “slip boundary condition” and have stimulated considerable interest in recent years. Ulmanella and Ho[5]found via experiments, the velocity slip for various micro-sized channels. The velocity at the wall is a function of shear rate, type of liquid and surface morphology. The possibility of temperature jump along with velocity slip was described by Bocquet and Barrat[6]. The velocity slip and temperature jump was modelled by Bocquet and Barrat[6]via the introduction of velocity slip length and temperature slip length terms, respectively. Many analytical and numerical methods have been employed to simulate a wide spectrum of slip flows. Wang[7]reported on the interaction of surface (momentum) slip on rotating Poiseuille and Couette flows, showing that for the former case slip enhances longitudinal flow rate at low rotation, but decreases it at high rotation, whereas in the latter case, longitudinal drag is reduced with greater slip. Nandy[8]studied unsteady flow of Maxwell fluid toward a permeable shrinking surface with Navier slip. Effects of hydrodynamic slip on the steady flow of an incompressible electrically conducting fluidpast a channel with porous plates are reported by Ibáñez[9].
Double-diffusive (thermo-solutal) convection flows are also of interest in many branches of engineering sciences including energy storage[10], nuclear reactor leakage hazards[11], nano-technological materials processing[12]and heat exchangers[13]. In natural convection heat and mass transfer, thermal and species buoyancy effects play a significant role. Slip flows with combined heat and mass transfer have also received some attention, primarily in chemical engineering applications. Wu and Chen[14]discussed transverse uniformity of concentration distribution of a solute in a solvent flowing along a straight pipe. They used Mei’s homogenization technique to find solutions for the concentration transport.et al.[15]presented concentration distribution of contaminant transport in wetland flows. They presented an analytical solution for the multi-dimensional concentration distribution by the method of mean concentration expansion.
Thermal radiation heat transfer arises in many chemical engineering processes. At a high temperature,thermal radiation may change the distribution of temperature in the boundary layer and this affects the heat transfer at the wall. A variety of radiative heat transfer models have been utilized for transport modelling. Due to the complexity of solving the integral-differential equation of radiative transfer these models are frequently algebraic flux approximations. Radiative flux was observed to significantly modify the critical Rayleigh and wave numbers and affect convection strongly. Mahmoud[16]employed the Rosseland diffusion flux model to study mixed convection-radiation flow from a horizontal permeable surface aligned parallel to a uniform free stream. Gupta et al.[17]used a variational finite element method and Rosseland flux model to simulate non-Newtonian radiative-convection flow from a shrinking polymeric sheet showing that the flow is accelerated substantially with increasing thermal radiation effect which also supplements energy transfer to the flow and enhances thermal boundary layer thickness. The Rosseland diffusion model was also implemented by Khan et al.[18]for radiative nanofluid slip flow.
In the present study a mathematical model is developed for buoyancy-driven mixed thermal convection-radiation slip flow from a vertical plate with species diffusion. A convective surface boundary condition is also prescribed and heat source/sink effects included. The Rosseland diffusion flux model is used for radiative heat transfer. Via Lie group theory methods the conservation equations are rendered into similarity ordinary differential equations and numerical solutions developed with shooting method. Selected solutions are verified with comparison to earlier non-slip flows.

Fig.1 Flow configuration and coordinate system
1. Mathematical flow model
Newtonian viscous incompressible double-diffusive mixed convection is studied. The geometry and the rectangular coordinatesand, and the corresponding velocity components,andand flow configuration are illustrated in Fig.1 (in whichi represents momentum whilerepresents thermal and concentration boundary layers, in general thermal and concentration boundary layer thickness are not the same). It is assumed that the uniform temperature of the ambient fluid is, the unknown temperature of the plate isand the left surface of the plate is heated from a hot fluid of temperatureor is cooled from a cooled fluidby the process of convection. This then yields a heat transfer variable coefficient. It is assumed that the thermal radiation is present in the form of a uni-directional flux, applied transverse to the wall surface and obeys the Rosseland diffusion approximation. This formulation allows the transformation of the governing integral-differential equation for radiative energy balance into a Fourier-type diffusion equation analogous to that describing heat conduction or electrostatic pote-ntial (Coulomb’s law). The model is generally applicable to optically-thick media in which radiation is only known to propagate a limited distance prior to experiencing scattering or absorption. Implicit in this approach is the assumption that refractive index of the medium is constant, intensity within the fluid is nearly isotropic and uniform and wavelength regions exist where the optical thickness is greater than five. It is further assumed that the concentration (low) of the ambient fluid is the uniform concentration, the unknown concentration of the plate isFluid properties are assumed to be invariant except density, which is assumed to vary only in those changes that drive the flow (i.e., the Boussinesq approximation). A heat source (or sink) is also present. The governing boundary layer equations based on scale analysis in dimensional form relevant to our problem may be presented as follows[19]:

Following Karniadakis et al.[20]to get physically realistic results, we adopt velocity slip boundary condition at the wall and hence the boundary conditions at the wall are:
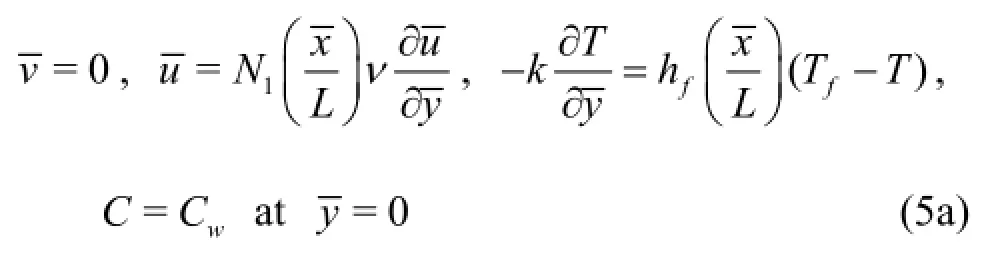
Based on problem description, the far field boundary conditions are
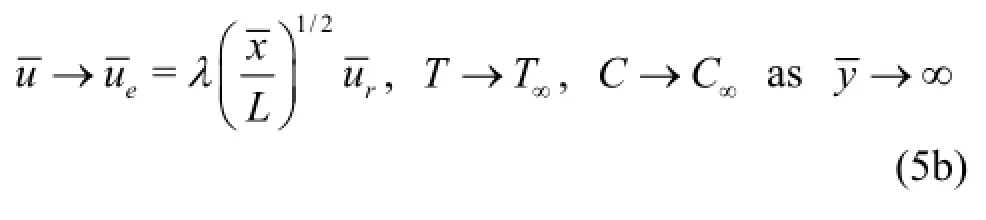
2. Transformation of model and lie group analysis
We introduce the following boundary layer variables to transform Eqs.(1)-(5) to dimensionless form.


The transformed boundary conditions in Eq.(5)become:
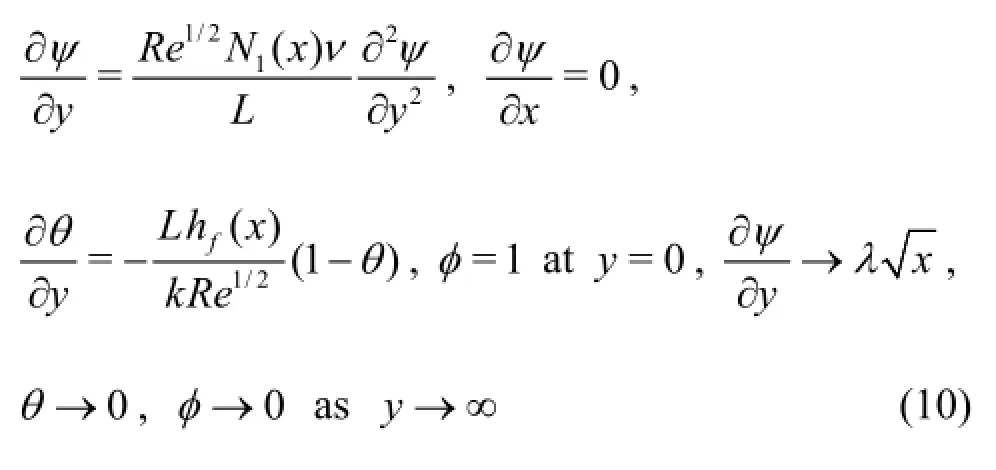
The transformed boundary layer equations and boundary conditions i.e., Eqs.(7)-(10) constitute a strongly coupled, highly nonlinear boundary value problem. Analytical solutions are extremely difficult. To obtain direct numerical solutions of these equations is also complicated and computationally expensive. Similarity solutions have proven to be an efficient tool to solve various transport problems. In view of this, we implement a linear group of transformations which combines the two independent variablesinto a single independent variable(similarity variable) and reduce Eqs.(7)-(10) into a system of coupled ordinary differential equations with the corresponding boundary conditions. Group theory methods proved to be efficient and very useful in recent years and have been successfully used to a wide range of complex flows in chemical engineering. In accordance with the group theory methodology, we scale all independent and dependent variables as follows[21]:
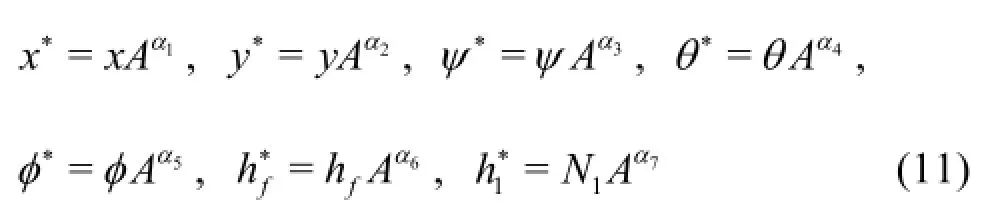
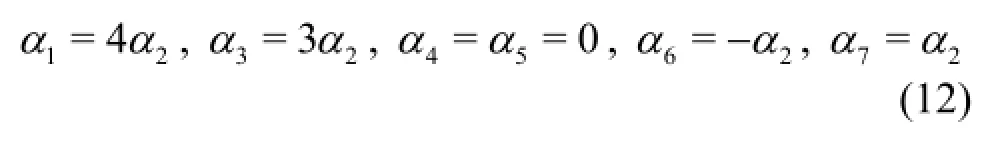
Now, we seek “absolute invariants” (functions having the same form before and after the transformation under this group of transformations[21]. An inspection of Eqs.(11) and (12) reveals that

This combination of variables is therefore invariant under this group of transformations and hence, is an absolute invariant. We denote this functional form as

Using the same argument, the other absolute invariants are:
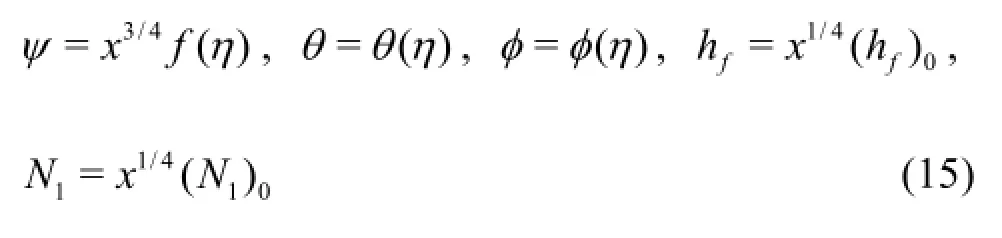
3. Governing similarity equations
Substituting Eqs.(14) and (15) into Eqs.(7)-(9),generates the following ordinary differential equations:
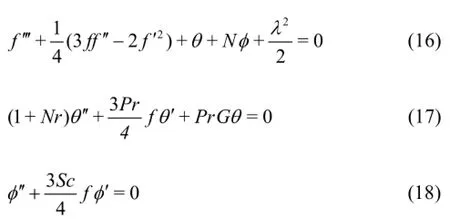
subject to the boundary conditions:
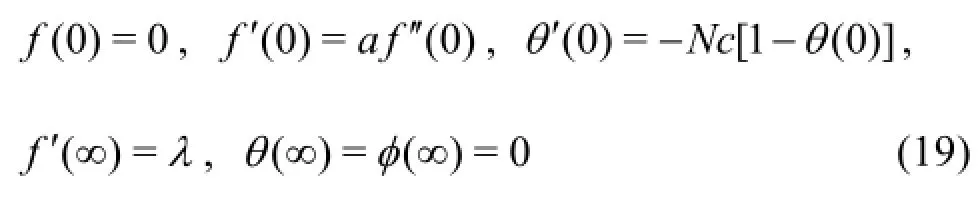
where primes denote differentiation with respect toHereis the convection-conduction parameter,is hydrodynamic slip parameter.
Examination of Eqs.(16)-(19) reveals some interesting special cases. In the absence of species diffusion i.e., neglecting the concentration equation and also negating heat source/sink effectand momentum slip, taking the isothermal, non-radiatingplate scenario, in the absence of free streamand under the following minor modification:
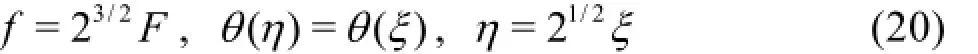
Equations (16)-(17) reduce to:
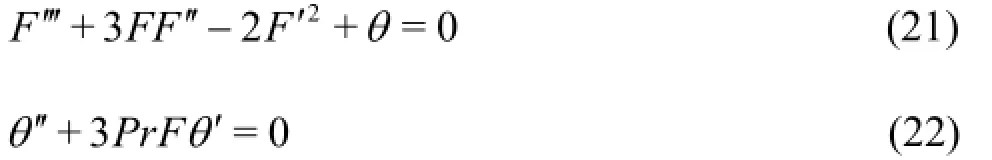
The simplified boundary conditions (19) contract to
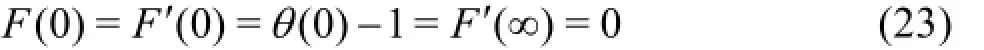
Equations (21)-(22) with the boundary conditions Eq.(23) correspond to the classical model of Ostrach[22]and provide an excellent benchmark for validation of the numerical solutions.
4. Quantities of physical interest
The physical parameters of interest in the present problem are the skin friction factor (surface shear stress),the local Nusselt number (surface heat transfer rate)and the local Sherwood number(surface species diffusion rate)all of which are derived from spatial gradient functions of velocity,temperature and concentration, respectively. The appropriate expressions are:
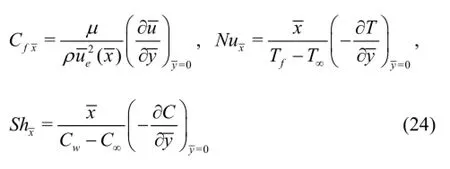
Using Eqs.(6), (14), (15), we have from Eq.(24):
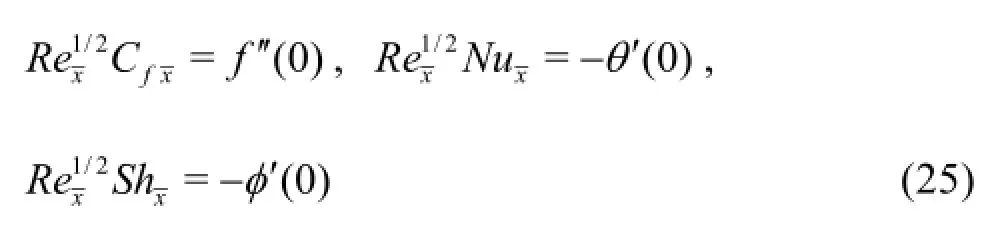
5. Results and discussion
Equations (16)-(18) with the boundary conditions(19) were solved numerically using the Runge-Kutta-Fehlberg fourth-fifth order numerical method provided in Maple 17 software. The step size was assumed to be 0.001 and the convergence criteria was taken as 10-6. The asymptotic boundary conditions, given by Eq.(19), were replaced by using a value of 12 for the similarity variableas follows

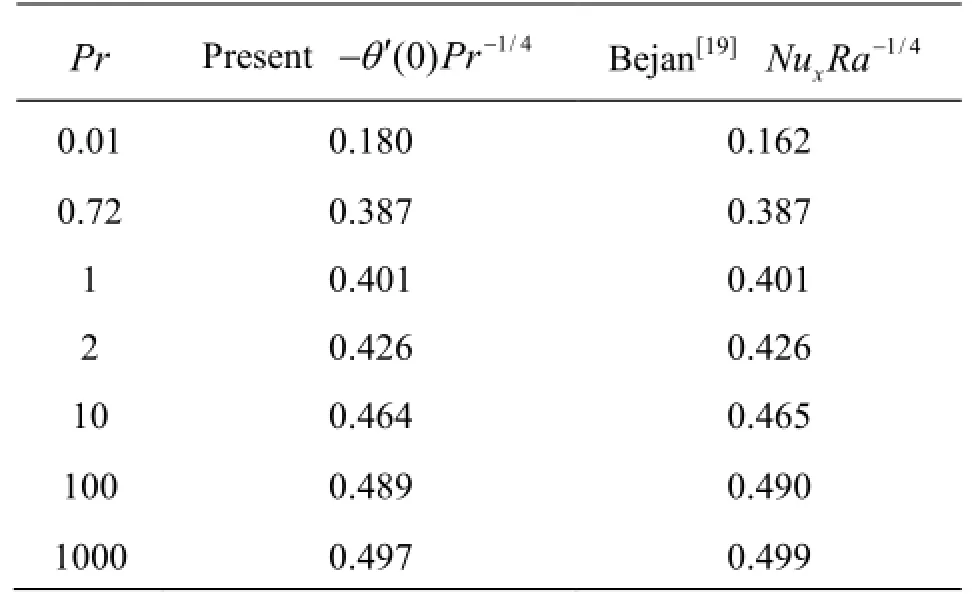
Table 1 Comparison of heat transfer rates for various Prandtl numbers withNc→∞
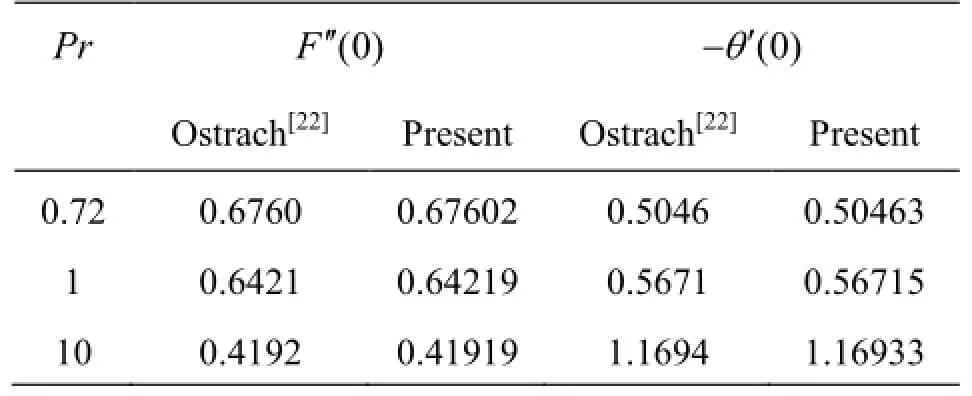
Table 2 Comparison of surface shear stress and heat transfer rate for different Prandtl numbers
Graphical results for the variation of the dimensionless velocity, temperature and concentration (species diffusion) fields with distance transverse to the plate are provided in Figs.2-16. Generally we prescribed the following parameter values:(hydrogen), unless otherwise stated. These correspond to buoyancy-assisted flow with thermal buoyancy force being twice the magnitude of species (concentration) buoyancy force, weak slip, weak heat generation, weak convective boundary condition, weak thermal radiative flux compared with thermal conductionheat transfer, carrier fluid of air and hydrogen gas as the diffusing species. Since bothandare less than unity, both species diffusivity and thermal diffusivity will exceed momentum diffusivity. Furthermore throughout the computations we consider the case of mixed convection i.e.,and there is moving free stream (velocity at the boundary layer edge is non-zero), as reflected in the free stream boundary condition in Eq.(19).
Table 3 Values ofandwhen
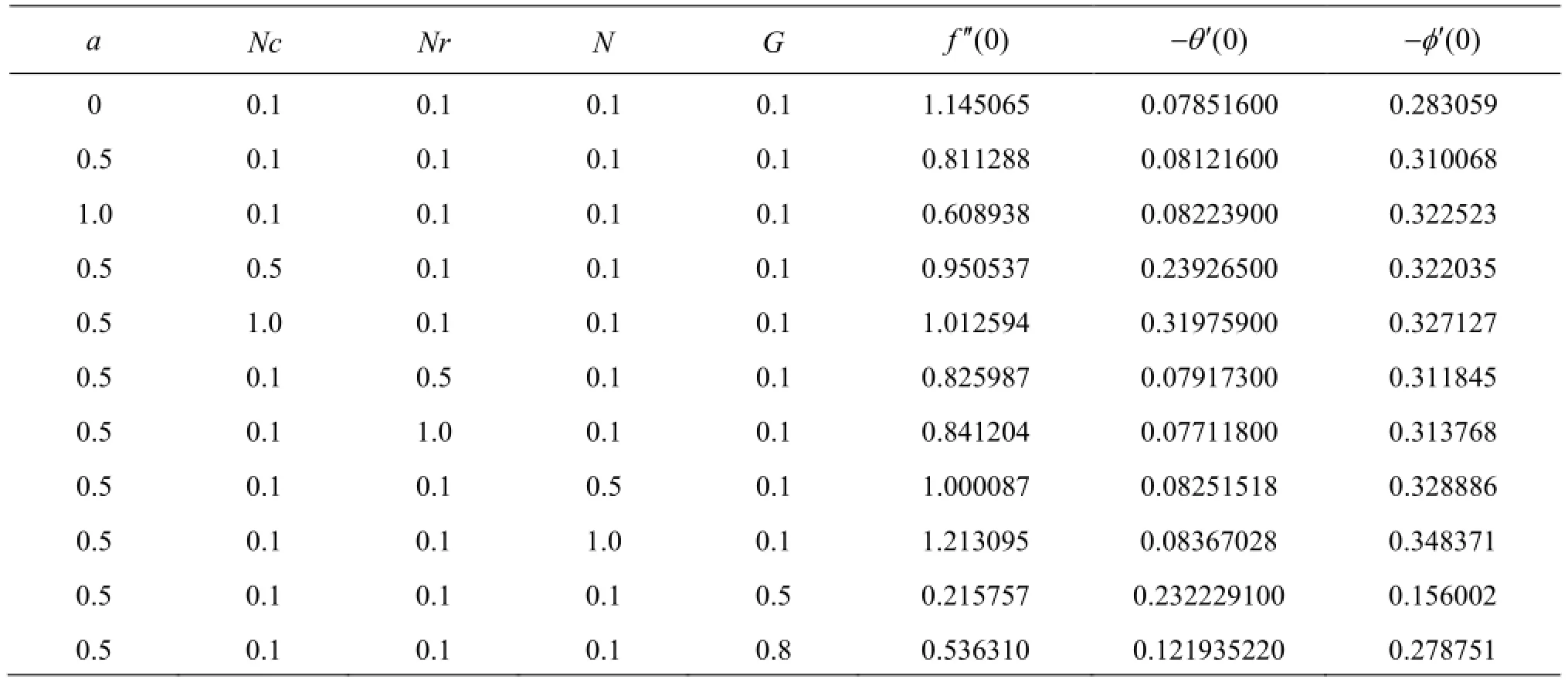
Table 3 Values ofandwhen
a Nc Nr N G (0)f′′ (0)θ′-(0)φ′-0 0.1 0.1 0.1 0.1 1.145065 0.07851600 0.283059 0.5 0.1 0.1 0.1 0.1 0.811288 0.08121600 0.310068 1.0 0.1 0.1 0.1 0.1 0.608938 0.08223900 0.322523 0.5 0.5 0.1 0.1 0.1 0.950537 0.23926500 0.322035 0.5 1.0 0.1 0.1 0.1 1.012594 0.31975900 0.327127 0.5 0.1 0.5 0.1 0.1 0.825987 0.07917300 0.311845 0.5 0.1 1.0 0.1 0.1 0.841204 0.07711800 0.313768 0.5 0.1 0.1 0.5 0.1 1.000087 0.08251518 0.328886 0.5 0.1 0.1 1.0 0.1 1.213095 0.08367028 0.348371 0.5 0.1 0.1 0.1 0.5 0.215757 0.232229100 0.156002 0.5 0.1 0.1 0.1 0.8 0.536310 0.121935220 0.278751

Fig.2 Effect of convection-conduction parameter on the dimensionless velocity (
Figures 2-6 illustrate the influence of the governing thermophysical parameters on velocity evolution in the boundary layer. With an increase in convectionconduction parameterthere is a significant acceleration in the boundary layer flow (Fig.2) in close proximity to the plate. A prominent peak arises near the plate and this is progressively displaced closer to the plate asis increased.anticipated further from the plate the influence ofvanishes.embodies the relative influence of thermal convection heat transfer to thermal conduction heat transfer.
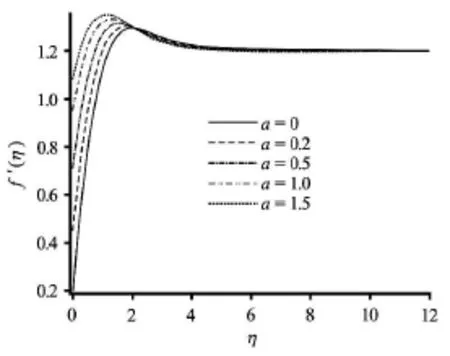
Fig.3 Effect of momentum slip parameter on the dimensionless velocity
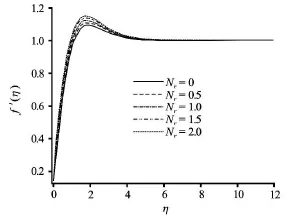
Fig.4 Effect of radiation-conduction parameter on the dimensionless velocity (
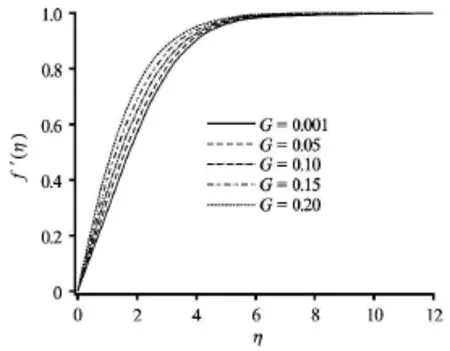
Fig.5 Effect of heat generation (source) parameter on the dimensionless velocity
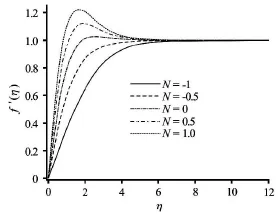
Fig.6 Effect of buoyancy ratio parameter on the dimensionless velocity

Fig.7 Effect of convection-conduction parameter on the dimensionless temperature
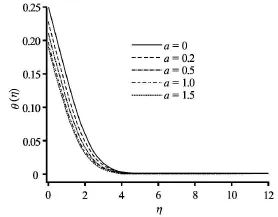
Fig.8 Effect of momentum slip parameter on the dimensionless temperature?
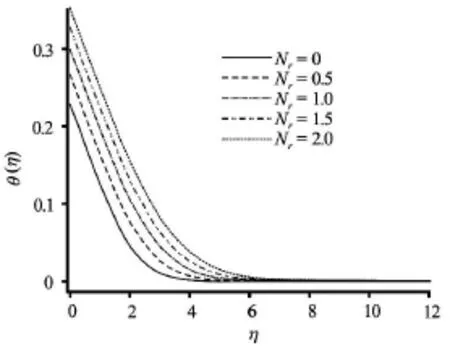
Fig.9 Effect of radiation-conduction parameter on the dimensionless temperature
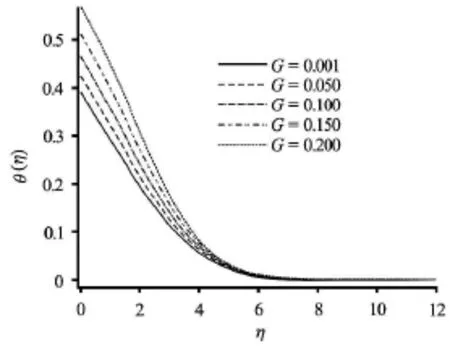
Fig.10 Effect of heat generation (source) parameter on the dimensionless temperature
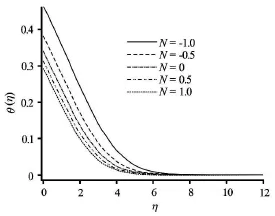
Fig.11 Effect of buoyancy ratio parameter on the dimensionless temperature
Figures 7-11 depict the distributions of temperature in the boundary layer with various parameters. A marked increase in temperature is generated with a rise in convection-conduction parameteras observed in Fig.7. The maximum enhancement is evidently at the plate. Thermal boundary layer thickness will therefore be increased. Conversely a noticeable reduction in temperature is seen with an increase in momentum slip parameter (Fig.8). Slip velocity has been shown to increase heat transfer rates from the bounding surface to the fluid as elucidated in Das. This is due to an increase in advection in a region where diffusion is dominant. This has also been observed by Turkyilmazoglu[8]. Figure 9 reveals that increasing presence of thermal radiation (i.e., larger values ofinduces a substantial heating of the fluid regime and elevates thermal boundary layer thickness considerably. Thermal diffusivity of the fluid medium is augmented by thermal radiation, which aids in transport of heat into the boundary layer leading to temperature enhancement. Due to the convective surface boundary condition at the plate (0.1) temperatures vary at the plate for each profile, but are clearly maximized for, for which thermal radiation contribution is double that of thermal conduction. An increase in heat source parameterin Fig.10 also aids thermal diffusion in the boundarylayer and strongly increases temperatures both at the plate and for some distance transverse to it. Fig.11 demonstrates that for buoyancy-opposed flowtemperatures are increased whereas for buoyancy-assisted flowthey are depressed. Thermal boundary layer thickness is therefore enhanced with increasingly vigorous buoyancy opposition.

Fig.12 Effect of convection-conduction parameter on the dimensionless concentration
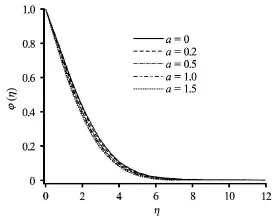
Fig.13 Effect of momentum slip parameter on the dimensionless concentration
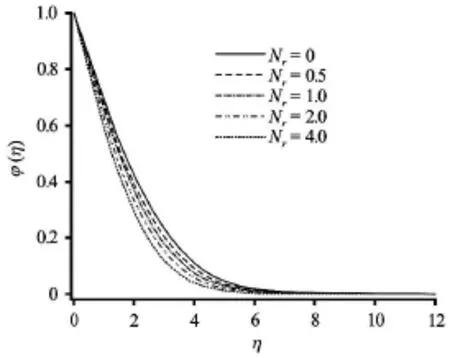
Fig.14 Effect of radiation-conduction parameter on the dimensionless concentration
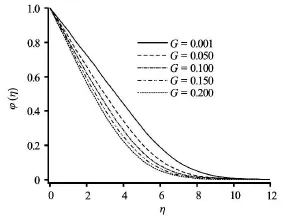
Fig.15 Effect of heat generation (source) parameter on the dimensionless concentration
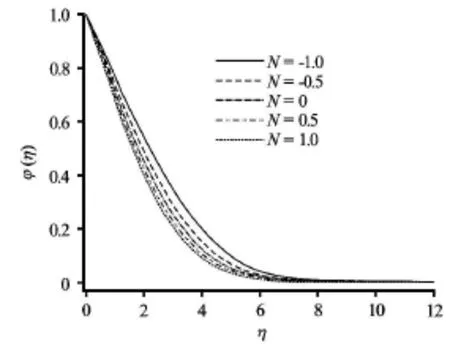
Fig.16 Effect of buoyancy ratio parameter on the dimensionless concentration
Figures 12-16 depict the distributions of the dimensionless concentration with various parameters. Concentration values are slightly depressed with increasing convection-conduction parameteras shown in Fig.12. Species diffusion is therefore opposed somewhat with increasing convection at the plate. Similarly a weak reduction in concentration is associated with a significant rise in momentum slip parameter(Fig.13). Species diffusion is therefore most efficient in the regime for the no-slip case. Concentration boundary layer thickness is therefore reduced with increasing velocity slip at the plate. Inspection of Figs.14, 15 shows that with increasing thermal radiationand heat generation, there is a fall in species concentrations. With buoyancy-opposed flowthe concentration boundary layer thickness is however enhanced (Fig.16) whereas the opposite is apparent with buoyancy-aided flows. In all the computations presented very smooth profiles have been achieved testifying to the satisfaction of convergence and the adequate specification of a far-fieldvalue of transverse coordinate,η.
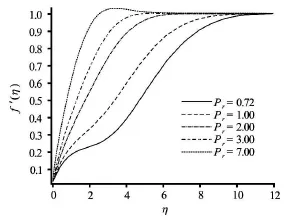
Fig.17 Effect of Prandtl number on the dimensionless velocity
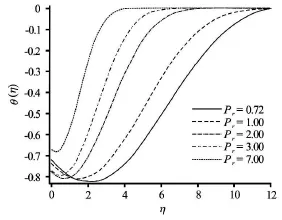
Fig.18 Effect of Prandtl number on the dimensionless temperature
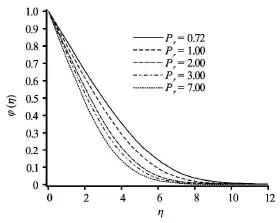
Fig.19 Effect of Prandtl number on the dimensionless concentration
Figurtes 17-19 depict the distributions of the dimensionless velocity, temperature and concentration with Prandtl number. Velocity (Fig.17) and temperature (Fig.18) are found to be increased whereas concentration (Fig.19) values are slightly depressed with increasing Prandtl number.
6. Conclusions
Numerical solutions have been presented for the nonlinear buoyancy-driven mixed convection heat and mass transfer in slip flow from a vertical surface with thermal radiation and heat source. Lie group theory has been employed to derive similarity equations. Very good correlation between the present numerical solutions and earlier classical computations of Ostrach[22]and Bejan[19]has been obtained. It has been observed that:
(1) A rise in momentum slip parameterelevates flow velocity but reduces temperature and concentration values.
(2) Increasing radiative-conductiveparameter increases velocity and temperature but lowers concentration.
(3) With higher values of convection-conduction parameterthe velocity is enhanced as is fluid temperature whereas concentration of the diffusing species is decreased.
(4) An increase in heat generation parameterleads to an acceleration of the flow and increasing temperature whereas it decreases concentration.
(5) Increasing positive values of buoyancy-ratio parameter(corresponding to buoyancy-aided flow) accelerates the flow but reduces temperature and concentration, the converse response is computed for increasingly negative values of(buoyancy-opposed flow).
The present study has considered Newtonian fluids. Future effort will be made to examine doublediffusive slip flows of viscoelastic fluids[23]and will be communicated immediately.
Acknowledgement
The authors acknowledge financial support from Universiti Sains Malaysia, (RU Grant No. 1001/PMATHS/811252).
References
[1] WANG C. Y. Flow due to a stretching boundary with partial slip-an exact solution of the Navier-Stokes equations[J]. Chemical Engineering Science, 2002, 57(17): 3745-3747.
[2] MUKHOPADHYAY S., Effects of slip on unsteady mixed convective flow and heat transfer past a porous stretching surface[J]. Nuclear Engineering and Design, 2011,241(8): 2660-2665.
[3] IRELAND P. M., JAMESON G. J. Foam slip on surfaces of intermediate or low wettability[J]. Chemical Engineering Science, 2009, 64(17): 3859-3867.
[4] KHALED A. R. A., VAFAI K. Analysis of oscillatory flow disturbances and thermal characteristics inside fluidic cells due to fluid leakage and wall slip conditions[J]. Journal of Biomechanics, 2004, 37(5): 721-729.
[5] ULMANELLA U., HO C. M. Molecular effects on boundary condition in micro/nanoliquid flows[J]. Physics of Fluids, 2008, 20(10): 101512.
[6] BOCQUET L., BARRAT J. L. Flow boundary conditions from nano- to micro-scales[J]. Soft Matter, 2007, 3(6): 685-693.
[7] WANG C. Y. The effect of slip on the flow in a rotating channel[J]. Chemical Engineering Communications,2013,200(4): 587-594.
[8] NANDY S. K. Unsteady flow of Maxwell fluid in the presence of nanoparticles toward a permeable shrinking surface with Navier slip[J]. Journal of the Taiwan Institute of Chemical Engineers, 2015, 52: 22-30.
[9] IBÁÑEZ G. Entropy generation in MHD porous channel with hydrodynamic slip and convective boundary conditions[J]. International Journal of Heat and Mass Transfer, 2015, 80: 274-280.
[10] BÉG O. A., UDDIN M. J. and RASHIDI M. M. et al. Double-diffusive radiative magnetic mixed convective slip flow with Biot and Richardson number effects[J]. Journal of Engineering Thermophysics, 2014, 23(2): 79-97.
[11] UNAL C., BOHL W. R. and PASAMEHMETOGLU K. O. Modeling of heat and mass transfer in accelerator targets during postulated accidents[J]. Nuclear Enginee- ring and Design, 2000, 196(2): 185-200.
[12]RANA P., BHARGAVA R. and BÉG O. A. Finite element simulation of unsteady magneto-hydrodynamic transport phenomena on a stretching sheet in a rotating nanofluid[J]. Proceedings of the Institution of Mechanical Engineers, Part N: Journal of Nanoengineering and Nanosystems, 2013, 227(2): 77-99.
[13] ZUECO J., BÉG O. A. and TAKHAR H. S. et al. Thermophoretic hydromagnetic dissipative heat and mass transfer with lateral mass flux, heat source, Ohmic heating and thermal conductivity effects: Network simulation numerical study[J]. Applied Thermal Engineering, 2009, 29(14): 2808-2815.
[14]WU Z., CHEN G. Q. Approach to transverse uniformity of concentration distribution of a solute in a solvent flowing along a straight pipe[J]. Journal of Fluid Mechanics,2014, 740: 196-213.
[15] WU Z., FU X. and WANG G. Concentration distribution of contaminant transport in wetland flows[J]. Journal of Hydrology,2015, 525: 335-344.
[16] MAHMOUD M. A. Variable fluid properties and thermal radiation effects on mixed convection flow over a horizontal surface[J]. International Journal for Computational Methods in Engineering Science and Mechanics,2010, 11(5): 299-303.
[17] GUPTA D., KUMAR L. and BÉG O. A. et al. Finite element simulation of mixed convection flow of micropolar fluid over a shrinking sheet with thermal radiation[J]. Proceedings of the Institution of Mechanical Engineers,Part E: Journal of Process Mechanical Engineering, 2014, 228(1): 61-72.
[18]KHAN W. A., UDDIN M. J. and ISMAIL A. I. M. Effects of radiation on Blasius slip flow of oxide nanofluids with Merkin boundary condition[J]. Proceedings of the Institution of Mechanical Engineers, Part N: Journal of Nanomaterials Nanoengineering and Nanosystems,2013, 227(1): 3-9.
[19] BEJAN A. Convection heat transfer (Chapter 4)[M]. 4th Edition, New York, USA: Wiley, 2013.
[20] KARNIADAKIS G., BESKOK A. and ALURU N. Microflows and nanoflows fundamentals and simulation[M]. New York, USA: Springer Science, 2005.
[21] UDDIN M. J., BÉG O. A. and AZIZ A. et al. Group analysis of free convection flow of a magnetic nanofluid with chemical reaction[J]. Mathematical Problems in Engineering, 2015, 2015: ID621503.
[22] OSTRACH S. An analysis of laminar free-convection flow and heat transfer about a flat plate parallel to the direction of the generating body force[R]. National Advisory Committee for Aeronautics, Report No. NACA-TR-1111, 1953,63-79.
[23] TRIPATHI D., BÉG O. A. A numerical study of oscillating peristaltic flow of generalized Maxwell viscoelastic fluids through a porous medium[J]. Transport in Porous Media, 2012, 95(2): 337-348.
May 6, 2015, Revised September 20, 2015)
* Biography: M. J. UDDIN (1974-), Male, Ph. D.,
Associate Professor
- 水动力学研究与进展 B辑的其它文章
- Theoretical analysis and numerical simulation of mechanical energy loss and wall resistance of steady open channel flow*
- Investigation of cavitation bubble collapse near rigid boundary by lattice Boltzmann method*
- A joint computational-experimental study of intracranial aneurysms: Importance of the aspect ratio*
- Oscillating-grid turbulence at large strokes: Revisiting the equation of Hopfinger and Toly*
- A robust WENO scheme for nonlinear waves in a moving reference frame*
- Numerical simulations of viscous flow around the obliquely towed KVLCC2M model in deep and shallow water*

