基于学前诊断的认知分析及教学设计实践研究——以“二元一次方程组及其解法”为例

☉上海市嘉定区南翔中学　王　欣

基于学前诊断的认知分析及教学设计实践研究——以“二元一次方程组及其解法”为例

☉上海市嘉定区南翔中学王欣

一、问题提出

《上海市中小学数学课程标准》指出：“课程要为学生提供多种学习经历，丰富学习经验.确立学生在学习中的主体地位，关注学生的已有经验和兴趣爱好、个性特长等发展特点.”好的数学课堂教学设计应关注到学生的已有经验和知识结构，这需要教师在课前设计学前诊断，了解学生对已有知识的掌握及对新知的认知程度，从而有针对性地设计教学，达到以学生为主体的有效课堂教学.本文以上海教育出版社六年级数学下册的“6.9二元一次方程组及其解法”的第一课时“代入消元法”为例，研究基于学前诊断的认知分析，设计教学.

二元一次方程组及其解法是在学生学习了一元一次方程及一元一次不等式组的基础上来进行学习的，并为后续的三元一次方程组的解法做铺垫.

本课时的教学目标是：理解二元一次方程组的有关概念，以及二元一次方程组的解的概念；能利用代入消元法熟练地解二元一次方程组；经历解二元一次方程组的过程，体验数学的化归思想.知道化归的基本方法——“消元”.在学会解一元一次方程的基础上，初步掌握运用“化归”思想解二元一次方程组，掌握“消元法”.

本节课的教学重点是“代入消元法”解二元一次方程组，难点是对“消元法”这一化归思想的理解.

二、学前诊断

（一）任务设计

学前诊断共设计5个问题（表1），且按如下梯度展开：

问题1是解一元一次方程的问题，其中任务Ⅰ是一道简单的解一元一次方程的问题，解答过程简单，其诊断目的是考查学生在学习二元一次方程组之前的知识基础；任务Ⅱ是一道含有常数a的一元一次方程问题，学生解答过程中需要将a与其他常数进行合并同类项的处理，并且体会用含有字母a的式子表示未知数x.其考查目的是学生能否掌握用含有字母的式子表示未知数（实际上，“代入思想”的第一步是将一个未知数（字母形式）用另一个未知数表示，本任务旨在考查学生“用字母表示未知数”的能力，也作为问题4中任务Ⅱ的铺垫）.

问题2～问题4是三道二元一次方程（组）的问题，每个问题均包含两个任务.任务Ⅰ是探索二元一次方程所有正整数解的问题，让学生体会二元一次方程解的不确定性；在任务Ⅱ中，附加了一个“关于x（或x与y）满足何种条件”的问题，让学生尝试探索同时满足两个一次方程的公共解.需要指出的是，首先，考虑到学生尚未正式接触二元一次方程组，附加的一元（或二元）一次方程在提问方式上尽量适应学生水平.其次，三道题目的设计是有一定层次性的：在任务Ⅰ中，x与y的系数逐渐增大（为避免复杂计算，基本保持在5以下且计算结果为整数）；在任务Ⅱ中，附加的“关于x（或x与y）满足何种条件”难度逐渐加大.其中，问题2中任务Ⅱ的任务设计在“代入思想”上有较强的提示性；问题3中任务Ⅱ的任务设计需要学生首先对x进行求解，但解答过程简单；问题4中任务Ⅱ的任务设计需要学生体会“用含有一个未知数（字母形式）的式子表达另一个未知数”，实际上，问题1中的任务Ⅱ为该任务做了一定的铺垫.

前测诊断试卷共下发33份，收回33份，有效试卷33份.

表1　前测任务设计

（二）认知分析

1.学生在问题1上的表现及其认知分析

学生在任务Ⅰ上的表现良好，全班33人均正确求出方程的解，正确率达100%.需要说明的是，由于该任务计算量不大，学生在该任务上的表现不能反映其“解决（较复杂）一元一次方程问题的能力”.但该任务的设计目的是考查学生能否计算简单的一元一次方程，排除“学生不会解一元一次方程”对问题2及问题3中任务Ⅱ的干扰.由于学生在该任务上的正确率为100%，我们可以基本认为，学生在“解简单一元一次方程”问题上有较好的知识基础，在后续问题2及问题3中任务Ⅱ的计算时，可以排除“学生不会求解简单一元一次方程”这一因素.

学生在任务Ⅱ上的作答表现如表2.我们发现，当方程中加入用字母表示的常数a，学生的正确率下降明显，只有48.5%的学生能够用含有字母a的式子表达未知数x（其中只有21.2%的学生对结果作了约分）.在解决二元一次方程组问题时（两个方程均含有2个未知数），作为“代入思想”的第一步，学生应明晰如何用一个未知数（字母）表示另一个未知数.结合学生在该任务上的表现，学生在“代入思想”第一步上已经面临了不小的问题，其中24.2%的学生令a为具体某一数值进行计算，说明学生对字母型常数a的理解存在一定的难度.此外，12.1%的学生计算错误，15.2%的学生不理解题意，表明在接下来的教学中需加强带有字母型常数方程的计算.

表2　学生在问题1任务Ⅱ上的典型表现

2.学生在问题2～问题4上的表现及其认知分析

（1）在任务Ⅰ上的表现.

学生在任务Ⅰ上的作答表现如表3.问题2～问题4中任务Ⅰ的正确率逐渐降低，这可能是由于方程系数逐渐增大造成的.平均23.3%的学生能正确地用含x的式子表示y（或用含y的式子表示x），求出所有的正整数解.平均仅37.3%的学生只能正确地用含x的式子表示y.而在此之后，学生的计算面临了新的困难：平均有16.2%的学生无法求出所有的正整数解（仅选择若干为正整数的x代入式子，求出的答案不完备），平均有11.1%的学生不会找到满足条件的x的值，进而代入求出相应的y.为此，笔者访谈了出现这种情况的几位学生.其中一位无法确定相应的x的值的学生A说：“我能对方程变形，但有两个未知数，又没有已知的x或y，我不知道怎么求.”只能找到部分整数解的学生B说：“我把方程变形后，知道x是正整数，所以我选择从x=1，2，3，…开始代入，但发现求得的y的值有整数、小数或分数时，就认为我的计算出现了错误，但又不知道怎么解决，就放弃不做了.”同样求解不完全的学生C说：“我认为二元一次方程的正整数解有无数个，所以写出一部分就可以了.”说明学生对二元一次方程的整数解的求解仍存在很大的困难，在本节课的教学设计中，仍需有重点的讲解.需要指出的是，一些学生尽管不能用x表示y（或用y表示x）进而用代入法进行计算，但其基本理解了“二元一次方程组的解是同时满足两个二元一次方程的公共解”，只是在求解方法上尚未掌握更加高效的“代入法”.比如，平均有26.2%的学生尝试用“凑”的办法凑齐满足条件的解（尽管这其中仅有一半的学生得出完备答案）.实际上，对于复杂问题，“凑出所有解”显然是低效甚至无效的策略，但持这些策略的学生在“方程组的解是公共的”上有了一定理解，有待加强的是其对“代入思想”的理解.

表3　学生在问题2～问题4任务Ⅰ上的典型表现

（2）在任务Ⅱ上的表现.

学生在问题2～问题4任务Ⅱ中的表现如表4.

在问题2中，只有9.1%的学生在计算中出现错误.此外，笔者在问题2中额外设计了一个任务（见表1）“y的值还有其他可能的结果吗？”有27.3%的学生认为“有其他可能”或“不确定”，这说明他们在“二元一次方程中，确定其中一个未知数时，另一个未知数有相应的唯一的值与它对应”的理解不到位，在后续的教学中应强调并巩固.

在问题3中，有87.9%的学生能求出x并代入第一个方程求解（尽管有3.1%的学生出现了计算错误），有12.1%的学生没有代入求解.

在问题4的任务Ⅱ中则出现了两个二元一次方程，学生本就对求一个二元一次方程的解存在困难，所以本题中有45.4%的学生不能理解题意，无法计算.12.1%的学生通过求两个二元一次方程的公共整数解求得答案，39.4%的学生选择通过凑出各个方程的整数解求出公共整数解.这说明学生对于接下来要学习的二元一次方程组的解的定义理解的很好，所以在教学设计中可简单带过.而对于用其中一个未知数表示另一个未知数并“代入”的方法，学生存在很大的困难，这也是本节课的重点，所以让学生顺其自然地想到用其中一个未知数表示另一个未知数并“代入”求方程组的解是本节教学设计重点要解决的问题，接下来的教学设计将会详细解释. 3.1%的学生也即有1位学生通过分别把两个方程用含x的式子表示y，令y相等，求出答案.这是对两个方程的公共解的另一种解读，不失为一种好方法，根本也是消元，在以后的教学中可以学习.

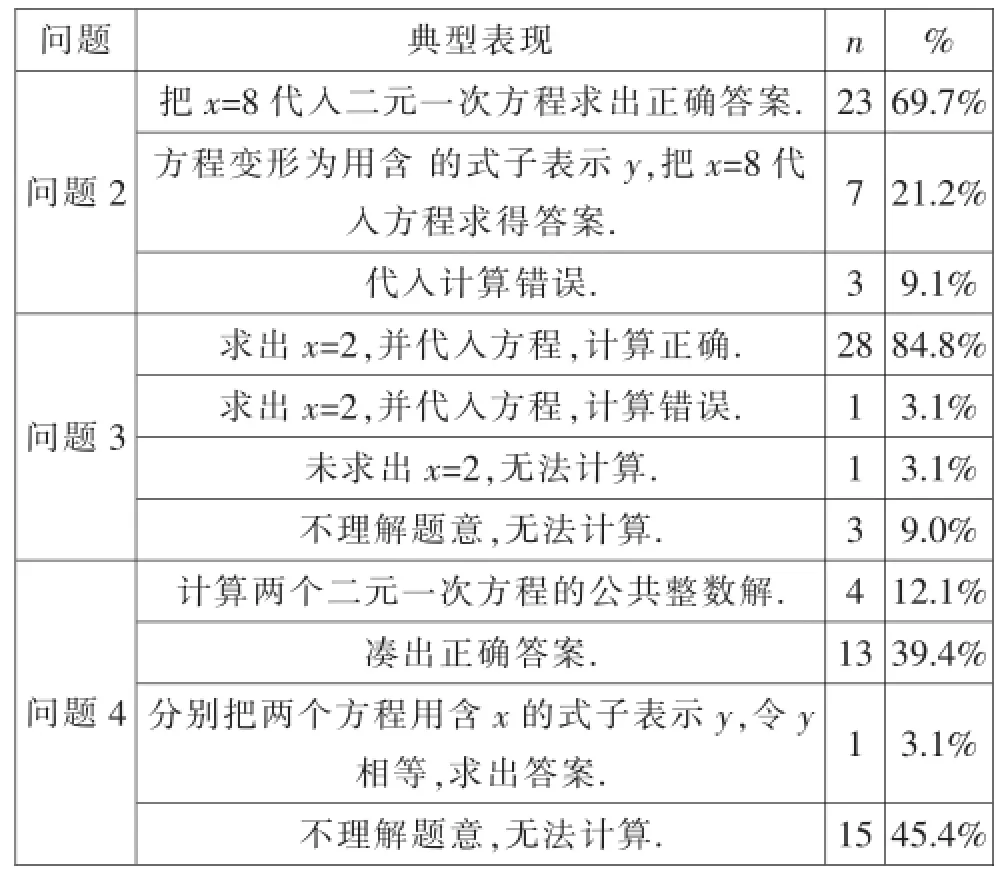
表4　学生在问题2～问题4任务Ⅱ上的典型表现

3.学生在问题5上的表现及其认知分析

表5　学生在问题5上的典型表现

从问题5上的学生表现可以看出，在遇到一次方程的应用时，45.4%的学生选择用一元一次方程的方法解决问题.18.1%的学生延续用小学时期用的假设法解决问题，而不选择方程，说明这部分学生的方程思想意识还不够强烈，在后续的教学及训练中应加强.有33.3%的学生能够列出两个二元一次方程解决问题，表明这些学生有强烈的方程意识，其中18.1%的学生根据题目的实际意义求出两个方程的公共整数解，得到正确答案.表明这部分学生在接受新知识及运用新知识的能力上是很高的.

三、教学路径设计

笔者从前测的诊断中，找出学生学习代入法解二元一次方程组遇到的难点，并依次设计突破相关难点的教学过程.

（一）二元一次方程的整数解

从前测中的问题2～问题4的任务Ⅰ的学生表现可知，仅平均23.3%的同学能依据方程变形求出二元一次方程的整数解.37.3%的学生能对方程正确变形，却无法确定相应全部的正整数解.所以本节课在学习“代入法”解二元一次方程组之前，选择鸡兔同笼问题作为情境引入，即教学诊断中的第5题解决二元一次方程的整数解的问题.

具体过程如下：

（2）解决问题情境中的问题，即求出二元一次方程组的解.易知二元一次方程x+y=35的正整数解有34个.对于二元一次方程2x+4y=94，假设笼子里全是鸡，也即y= 0，易知x=47，所以根据实际意义可知，1≤x≤47，且x只取正整数，有47种可能，但这47种可能里只有部分x，满足y也是正整数.同理假设笼子里全是兔子，也即x=0，则1≤y≤23，且y只能取正整数，y有23种可能，所以我们选择把原方程变形为用含y的式子表示x，即x=47-2y，令y= 1，2，3，…，求出相应的x的值.从而求出公共解.该情境既引入了二元一次方程组、二元一次方程组的解的定义，又解决了求二元一次方程正整数解时如何确定其中一个未知数的值的问题.

（二）“代入法”求二元一次方程组

（1）解下列方程组：

学生在教学诊断中问题2～问题4的任务Ⅱ中的表现为：问题2中任务Ⅱ的计算正确率为90.1%，问题3中任务Ⅱ的计算正确率为84.8%，表明大多数学生对于二元一次方程组，若其中一个为一元一次方程，都能理解并解决.所以在引入二元一次方程组后，设计①、②题做为引入，第③题进一步给出其中一个方程用含x的式子表示y的形式，引导学生采取代入法替换y，达到消元的目的.第④题给出依据第③题中的式子y=x-1回归到一般的二元一次方程的形式，让学生比较两题异同，逆推到变形代入，从而引出对一般二元一次方程组代入消元的方法.第⑤题引导学生针对一般的二元一次方程组如何选择方程变形代入消元.从而较为顺利自然地解决本节课的重点及难点.

四、教学效果检测及教学设计反思

（一）任务设计

教学效果检测是基于学前诊断作出的比较研究.依据学前诊断的任务设计，为方便数据对比，设计教学效果检测.其中，效果检测中题目的程度变的复杂，即问题1中出现较为复杂的括号，问题2～问题4中未知数系数为大于5的整数，加大了计算难度.本试卷中的问题5类似于学前诊断中的问题5，在列方程时，系数中出现小数，加大了计算难度，综合考查学生列方程解应用题的能力，方便比较学生前后差异.

（二）认知分析

表6　后测任务设计

试卷下发32份，收回32份，有效试卷32份.

1.学生在问题1上的表现及其认知分析

学生在题目1的第（1）小题有30人回答正确，即有90.9%的正确率，而9.1%的人出现了错误，说明仍有小部分学生在解决较复杂的一元一次方程的问题时，还存在一定的问题.需要在后续的学习中加强练习.

学生在任务Ⅱ上的表现如表7所示，从表7与前侧（表2）相比较可知，学生在计算带有字母a的常数时，正确率有了一定的提高；令a为某一数值的学生有所减少；但出现了4例用未知数x表示a，说明这部分学生并未理解题意；同时计算错误的人数增加了，说明学生在解决较复杂的一元一次方程时，出现了一定的困难，在后续练习中需加强巩固.

表7　学生在任务Ⅱ上的表现（后测）

2.学生在问题2～问题4上的表现及其认知分析

由表8可知，平均62.5%的学生能正确地用含x的式子表示y（或用含y的式子表示x），求出所有的正整数解，3.1%的学生不能正确地将方程变形，7.3%的学生凑出整数解，仍有14.6%的学生无法确定x的取值，不能求出所有的解.表明教学相对成功，但后续工作中仍需要加强练习.

表8　学生在问题2～问题4任务Ⅰ上的典型表现

学生在问题2～问题4中任务Ⅱ的表现见表9.

由表9知，学生在问题2中的正确率有很大的提高，但仍有12.5%的学生对y否有其他值不能理解.问题4中有87.5%的学生能够正确地列出二元一次方程组，说明大部分学生对二元一次方程组的理解还算到位，只有59.4%的学生计算正确，说明学生对于新知识中的计算仍需加强.

表9　学生在问题2～问题4任务Ⅱ上的典型表现

3.学生在问题5上的表现及其认知分析

表10　学生在问题5上的典型表现

表10中学生的正确率为78.1%，所以，学生对于二元一次方程组的“代入法”已基本掌握.表明课堂效果较好，教学设计相对成功.

（三）教学设计反思

基于学前诊断与学后检测的比较分析可知，基于学前诊断的认知分析有针对性地设计教学过程，在教学上能够真正做到以学生为主体，并有效抓住教学重点，突破教学难点，教学效果也显示教学相对成功.但也有值得反思的地方：（1）在做学前诊断中的问题2～问题4时，学生大部分时间都在解决求整数解的问题，而没有考虑两个二元一次方程间的关系，说明诊断问题中的重点失之偏颇.（2）此种方法不适合针对每一节课，在如何快速收集资料等方面仍需不断改进.H