从解题思考走向解题教学的研讨——以2016年江苏苏州中考第27题为例

☉江苏常熟市周行学校　黄欲涵

从解题思考走向解题教学的研讨——以2016年江苏苏州中考第27题为例

☉江苏常熟市周行学校黄欲涵

一、写在前面

每年各地新中考题出来之后，各大专业期刊都有相当篇幅的解题研究文章，这些文章对于不同解法、考题变式、结构洞察都有充分的探讨，然而，对于这类文章，如果能从解题思考走向解题教学的研讨，则可以丰富解题研究的视角，也有助于使解题研究的成果更好地服务于解题教学.本文以苏州中考一道考题为例，先给出思路突破，再展开解题教学的相关思考，与同行研讨.

二、考题及思路突破

（1）如图1，连接DQ，当DQ平分∠BDC时，t的值为______.

（2）如图2，连接CM，若△CMQ是以CQ为底的等腰三角形，求t的值.

图1

图2

图3

（3）请你继续进行探究，并解答下列问题.

①证明：在运动过程中，点O始终在QM所在直线的左侧；

②如图3，在运动过程中，当QM与⊙O相切时，求t的值，并判断此时PM与⊙O是否也相切，说明理由.

1.思路突破

（1）当DQ平分∠BDC时，QP=QC，如果能用含t的式子表示它们，就可以贯通思路了.先根据点P的运动速度，用含t的式子表示BP，得BP=4t，于是在Rt△BPQ中思考，这是一个“3，4，5”式的直角三角形，于是，PQ=3t，BQ=5t，于是CQ=3t，根据CQ+BQ=BC可得方程3t+5t=8，则t=1.

图4

（2）解读条件“△CMQ是以CQ为底的等腰三角形”，即“CM=MQ”.把目光聚焦在△CMQ中思考，重新构造图4.

（3）可以发现，前两问与动点O、⊙O是无关的，从（3）开始，有了关系，而且①需要证明点O始终在QM所在直线的左侧.先做“目标解析”，设直线MQ交CD于K点（如图5），问题的目标就是证明点O在点K的左侧，也即证明OC大于KC！

图5

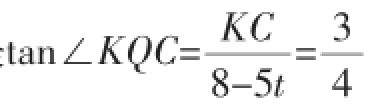
②如图6，在运动过程中，设QM与⊙O相切于G点，交CD于J点，把目光聚焦在Rt△OGJ和Rt△QCJ中，分离出局部图形（如图7）.

图6

图7

在图7中，Rt△OGJ和Rt△QCJ仍然是“3，4，5”式的三角形，用含t的式子分别表示CJ、OJ.CJ=，OC=6-3t，（事实上，这里的求解与上一问的求解思路是一致的）.把目光聚焦到Rt△OGJ中，

继续思考最后一个有挑战的问题“此时PM与⊙O是否也相切”，我们先做目标解析，如果相切，则一定有点O在∠PMQ的平分线上，接下来的演算向这个目标进发.

图8

2.解后反思

第一，熟悉“3，4，5”式直角三角形的性质，有助于思路突破.本题各个小问中都会涉及大小不同的特殊直角三角形，如果不对这些直角三角形三边之比保持敏感，则会影响思路获取或解题速度.比如所给的两个动点的运动速度4cm/s和3cm/s，都是命题者精心编拟的，目的是让解题者与“3，4，5”式直角三角形发生关联，且便于运算.

第二，注意图形动态变化后的位置，便于构造精准图形，有利于获取思路.比如正方形PQMN的大小在不断变大，相应的点M、Q的位置需要认真构思.此外，动点P、O是同时运动的，但运动速度不同，这也是解题时要注意的.

三、教学思考

1.解题教学要拓展概念的内涵与外延

从当前的教学研究和案例写作来看，概念教学被很多教师所重视，特别是对新授课期间的概念教学研究的热情高涨，有些专业期刊甚至针对概念教学开展专题征文、案例评析，这些都对概念教学的研究有很好的促进作用.但是，作为概念教学的必要跟进，解题教学中对概念的深入与拓展还是值得关注的，比如在解题教学中，重视引导学生回到概念去解题就是十分有必要的，像上文中的考题解析一样，重视回到勾股定理构造方程固然十分重要，但是作为特殊直角三角形，善于发现“3，4，5”，灵活运用锐角三角形函数构造方程或比例式显示可以看成是勾股定理这一核心概念的必要深化与发展，值得重视.

2.解题教学要重视“目标解析”意识

解题教学除了训练学生学会解具体的一道题，还需要有更多教学目标的追求，比如通过学习解题走向学会解题，并领会一类题的解法、策略，感悟思想方法.就上面的考题解答来说，由于考题的设问指向都需要“目标解析”，比如（2）“若△CMQ是以CQ为底的等腰三角形，求t的值”，目标解析就是“当CM=MQ时，求t的值”；再如（3）①的“证明”，本质是判断点O在点K的左侧（如图5）.根据我们多年的教学经验，不少解题有困难的学生，往往就是不能顺利进行目标解析造成解题思路受阻，这就需要教师在解题教学环节，要有意识地安排“目标解析”的提问或展示环节，让“目标解析”的能力和意识都得到训练.

3.解题教学适当安排跟进变式的检测

为了追求较好的解题教学效果，在学生听懂的基础上，还可以安排跟进变式的检测，反馈学生是否对这类问题真正掌握，以下就给出上述考题的一种跟进变式检测，供研讨.

变式题：如图9，在矩形ABCD中，AB=6cm，AD=8cm.点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上.

（1）如图9，当MQ=QC时，t的值为______.

（2）连接CM，MQ=MC，求t的值.

①若直线QM交边CD于K，比较OC、KC的大小.

②在运动过程中，当QM与⊙O相切时，小舟同学发现：此时PM与⊙O也是相切的关系.请判断“小舟发现”的真假，并说明理由.

图9

四、结束语

得益于网络的普及，最新的中考试题在网上传播得很快，不少师生、解题爱好者都对解题保持较高的热情，正如本文的探讨一样，作为抛砖引玉，期待广大同行不满足于解题层面的探讨，还要深入到解题教学的研讨，特别是针对考题展开变式教学的思考.当然，我们的努力还是初步的，期待批评指正.

1.周礼芳.重视教材“活动”材料，追求变式教学效率——以一道中考模考卷压轴题为例［J］.中学数学（下），2015（6）.

2.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

3.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

4.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.Z