潺潺流水在溯源——对一个几何模型及其应用的探索

☉河北晋州市实验中学　苑建广

潺潺流水在溯源——对一个几何模型及其应用的探索

☉河北晋州市实验中学苑建广

一、模型展示

在图1中，有△DMB∽△BNE.延长BM到A，使MA= MB；延长BN到C，使NC=NB；取AC的中点P.连接PM、PN、PD、PE、DE.则有△DPE∽△DMB∽△BNE.

证明：由已知条件，易知：

图1

所以△DMP∽△DBE.

类似地，可得△PNE∽△DBE.

则∠MDP=∠BDE，

∠PEN=∠DEB.

则∠PDE=∠MDB，

∠PED=∠NEB=∠MBD.

则△DPE∽△DMB∽△BNE.

当图形变化为其他情形时，只需对推证∠DBE=∠DMP的过程稍作调整即可.此处不再赘述.

以该模型为基础，构建的中考（模拟）题已经枚不胜举.为了体会模型与具体题目之间的内在联系，可以借助几何画板等数学软件制作动态图形，使其中的点D可以控制△DMB的形状，点A可以控制△DMB的大小与位置，点E可以控制△BNE的大小与位置.

二、模型应用

例1（2015年黑龙江·齐齐哈尔卷）如图1-1所示，在正方形ABCD和正方形CGEF中，点B、C、G在同一条直线上，M是线段AE的中点，DM的延长线交EF于点N，连接FM，易证：DM=FM，DM⊥FM（无需写证明过程）.

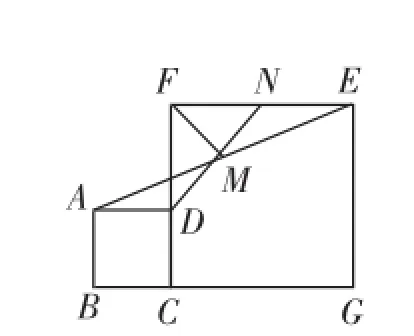
图1-1

图1-2

（1）如图1-2，当点B、C、F在同一条直线上，DM的延长线交EG于点N，其余条件不变时，试探究线段DM与FM有怎样的关系.请写出猜想，并给予证明.

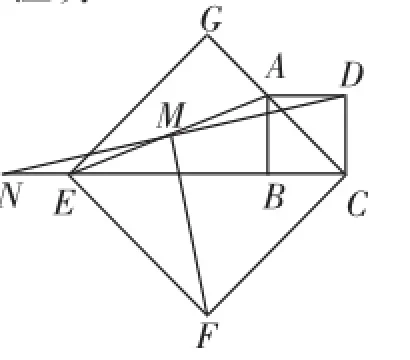
图1-3

（2）如图1-3，当点E、B、C在同一条直线上，DM的延长线交CE的延长线于点N，其余条件不变时，探究线段DM与FM有怎样的关系.请直接写出猜想.

分析：调整模型中点D的位置，使∠DMB=90°，DM=MB；调整点E的位置，使A、B、C共线，再补充完善图形，使四边形BXAD和四边形BYCE成为正方形，如图1-4所示，此时的模型与图1-2整体构造无异，只是字母不同罢了.借助模型之处理思路：易知△DPE∽△DMB∽△BNE，而△DMB、△BNE均为等腰直角三角形.对于图1-2，自然有△FMD是等腰直角三角形，即DM⊥FM且DM=FM.

调整模型中点D的位置，使∠DMB=90°，DM=MB；调整点E的位置，使∠ABC=45°，再补充完善图形，使四边形BXAD和四边形BYCE成为正方形，如图1-5所示，此时的模型与图1-3整体构造无异，只是字母不同罢了.借助模型之处理思路：易知△DPE∽△DMB∽△BNE，而△DMB、△BNE均为等腰直角三角形.对于图1-3，自然有△FMD是等腰直角三角形，即DM⊥FM且DM=FM.

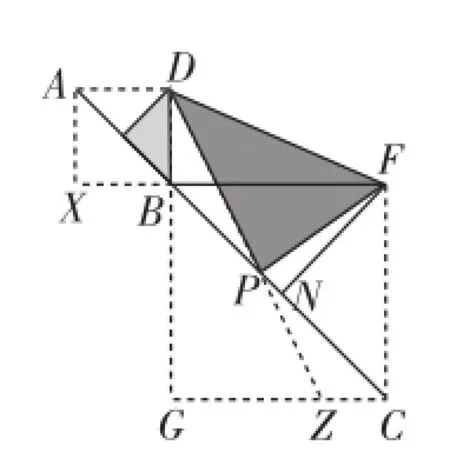
图1-4

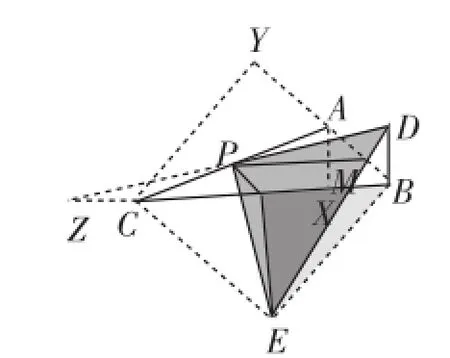
图1-5

运用此法解题，原题中的点N及与之相关的线段MN、EN是冗余条件.而对于其他思路，则可能并非多余.

例2（2015年江苏·扬州模拟卷）操作与证明：如图2-1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF.取AF的中点M、EF的中点N，连接MD、MN.

（1）连接AE，求证：△AEF是等腰三角形.

猜想与发现：

（2）在（1）的条件下，请判断MD、MN的数量关系和位置关系，得出结论.

结论1：DM、MN的数量关系是_______；

结论2：DM、MN的位置关系是_______.

拓展与探究：

（3）如图2-2，将图2-1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由.

图2-1

图2-2

分析：（1）容易证明.我们直接面对（2）、（3），感受其与模型的内在联系.

调整模型中点D的位置，使∠DMB=90°，DM=MB；再调整点E到线段AB上，并补充完善图形，使四边形BXAD成为正方形，△CBY成为等腰直角三角形，如图2-3所示，此时的模型与图2-1整体构造无异，只是字母不同罢了.借助模型之处理思路：易知△DPE∽△DMB∽△BNE，而△DMB、△BNE均为等腰直角三角形.对于图2-1，自然有△DMN是等腰直角三角形，即DM⊥MN且DM=MN.

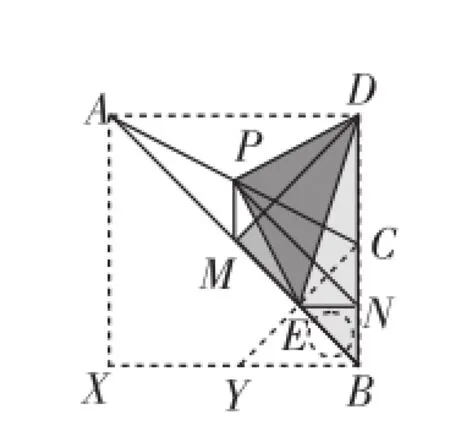
图2-3

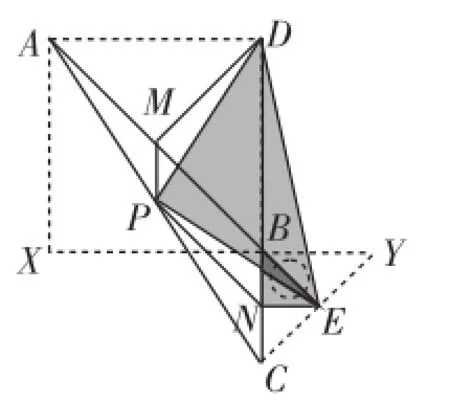
图2-4

调整模型中点D的位置，使∠DMB=90°，DM=MB；再调整点E到线段AB的延长线上，并补充完善图形，使四边形BXAD成为正方形，△CBY成为等腰直角三角形，如图2-4所示，此时的模型与图2-2整体构造无异，只是字母不同罢了.借助模型之处理思路：易知△DPE∽△DMB∽△BNE，而△DMB、△BNE均为等腰直角三角形.对于图2-2，自然有△DMN是等腰直角三角形，即DM⊥MN且DM=MN.

例3（2015年福建·晋江模拟卷）问题：如图3-1，将菱形ABCD和菱形BEFG拼接在一起，使得点A、B、E在同一条直线上，点G在BC边上，P是线段DF的中点，连接PG、PC.已知∠ABC=120°.

（1）直接写出图3-1中线段PG与PC的位置关系及∠PCG的大小.

（2）将图3-1中的菱形BEFG绕点B顺时针旋转，使点E恰好落在CB的延长线上，原问题中的其他条件不变（如图3-2）.你在（1）中得到的两个结论是否仍成立？写出你的猜想并加以证明.

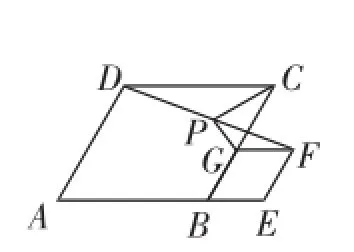
图3-1

图3-2

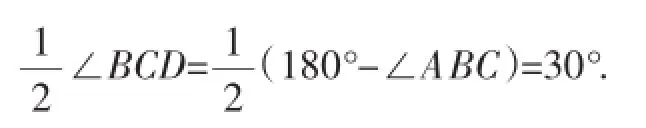
图3-3

图3-4

例4（2015年辽宁·葫芦岛卷）在△ABC中，AB= AC，点F是BC的延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG.

（1）如图4-1，当∠BAC=∠DCF=90°时，直接写出AG与DG的位置和数量关系；

（2）如图4-2，当∠BAC=∠DCF=60°时，试探究AG与DG的位置和数量关系；

（3）当∠BAC=∠DCF=α时，直接写出AG与DG的数量关系.

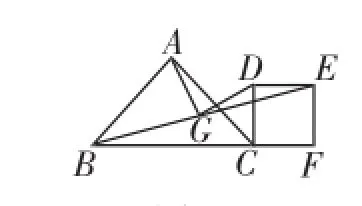
图4-1

图4-2

分析：（1）和（2）是（3）的特殊情形.我们直接面对（3），感受其与模型的内在联系.

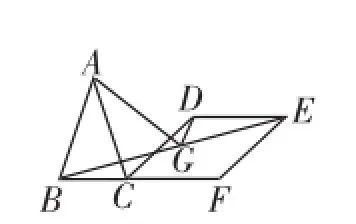
图4-3

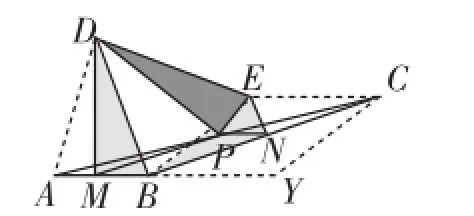
图4-4

【点评】数学教师要想提高教学实效，需手握两把利剑——“善变”和“深挖”.

“善变”对应变式教学，是中国数学教育传统而有效的做法.从一个模型开始，展开万千变化，构造出众多似曾相识却又面孔陌生的新题目，显然是一种命题的艺术.但“万变不离其宗”，由于我们在日常解题中，通过对比已经做过的题目之间的联系，“深挖”其本质，实现了对数学研究对象的深层解构，发现了存在于其中的数学模型，所以在面对形形色色的与之相关的问题时，才有了思维的洞察力，能够“透过表面现象看出本质”，通过化归和完善图形，找到问题的通用解法.

那么，该模型的本质究竟是什么呢？如何在未来的解题中顺利提取出该模型，从而化生为熟，运用通解，顺利解决此类问题呢？

一方面，模型中的两个已知相似三角形△DMB和△BNE的对应关系为点D对应点B，点M对应点N，点B对应点E，有一个非对应的顶点（B）是共用的，且在△DMB中沿周界D→M→B→D转动的方向与在△BNE中沿周界B→N→E→B转动的方向是一致的，均为逆（或顺）时针方向.

另一方面，点P是把对应边BM和BN各延长一倍分别至点A和C后所取的AC的中点.

这时，点P与顶点D和E组成的三角形（△DPE）是与原来的两个相似三角形（△DMB和△BNE）相似的，且在△DPE中沿周界D→P→E→D转动的方向仍与前述方向具有一致性.

要在形形色色、纷繁复杂的图形中发现并抽取出该模型就要抓住几个关键信息，一是中点P，二是两个相似三角形△DMB和△BNE，且其中M和N分别是BA和BC的中点.

在上述各个例题中，模型多是不明显的存在着，需要通过连接已知正方形（或菱形）的对角线，或取已知等腰三角形底边上的高来构造出点M和点N，这时模型才能浮出水面.抽取模型是最为关键的步骤.此步骤完成后，就是把对模型的证明过程向具体问题的迁移了，只要熟练掌握了模型的证明，在迁移中对角的等量关系和线段之间的等量或比例关系作适当调整，是很容易完成证明的.如果我们对这种利用模型解决此类问题的思路与标准答案对比，往往会发现利用模型解题的方法非常奇巧，简洁清新.

数学题海深阔无边.以有限的生命，数学题是解不完的.倘若在做过一部分题目后，深入反思，发现问题间的联系和本质，就能牵一发而动全身，手握“源”，从而从容应对“流”.这不恰恰相当于掌握了更多的定理，有了更多的解题武器了吗？教师之教和学生之学都应在这方面下大功夫，溯本求源，去感受和研究题目的本质与内涵，实现化归，而不是沉入题海，难以自拔.归曰：“潺潺流水在浚源”.

文末，提供两例相关问题.请读者予以探究.

练习1：（2008年北京卷）请阅读下列材料：

问题：如图5-1，在菱形ABCD和菱形BEFG中，点A、B、E在同一条直线上，P是线段DF的中点，连接PG、PC.若∠ABC=∠BEF=60°，探究PG与PC的位置关系及的值.

小聪同学的思路是：延长GP交DC于点H，构造全等三角形，经过推理使问题得到解决.

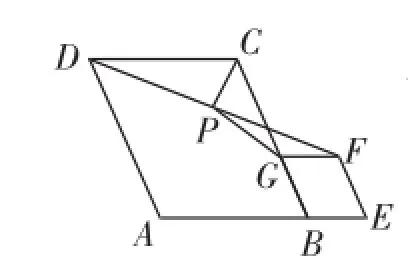
图5-1

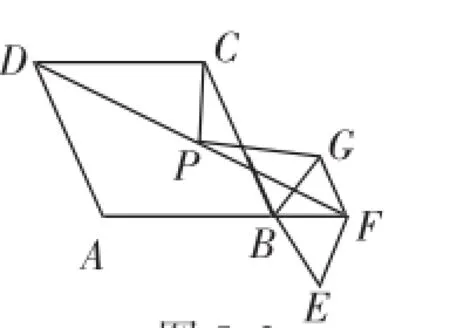
图5-2

请你参考小聪同学的思路，探究并解决下列问题：

（2）将图5-1中的菱形BEFG绕点B顺时针旋转，使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上，原问题中的其他条件不变（如图5-2）.你在（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明.

练习2：（2011年湖北·武汉模拟卷）如图6-1～图6-2，四边形ABCD为正方形，△BEF为等腰直角三角形（∠BFE=90°，点B、E、F按逆时针排列），点P为DE的中点，连接PC、PF.

（1）如图6-1，点E在BC上，则线段PC、PF的数量关系为______，位置关系为_____（不用证明）.

图6-1

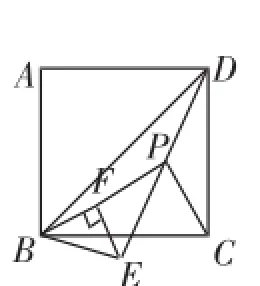
图6-2

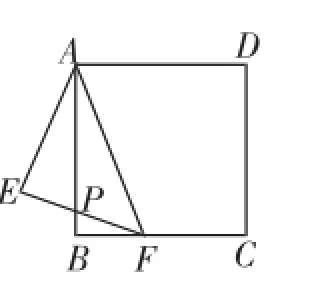
图6-3

（2）如图6-2，将△BEF绕点B顺时针旋转a（0°＜a＜45°），则线段PC、PF有何数量关系和位置关系？请写出你的结论，并证明.

（3）如图6-3，△AEF为等腰直角三角形，且∠AEF= 90°，△AEF绕点A逆时针旋转过程中，能使点F落在BC上，且AB平分EF，直接写出AE的值是________.

1.钱德春.初中数学“模型”教学之我见［J］.中学数学（下），2016（5）.

2.闵彦利.一题多变，拓展思维——培养学生创新思维能力的有效途径［J］.中学数学（下），2016（4）.

3.苑建广.精心雕琢命题方式切实考查数学能力——2011年中考数学特色题归类赏析［J］.教育实践与研究（B版），2011（11）.

4.苑建广.信息转化——问题解决的核心策略［J］.中国数学教育（初中版），2012（3）.Z