多重时滞富营养化生态模型的稳定性与分支分析

杨纪华,刘媚

(1.宁夏师范学院数学与计算机科学学院,宁夏固原756000)

(2.北京师范大学数学科学学院,北京100875)

多重时滞富营养化生态模型的稳定性与分支分析

杨纪华1,2,刘媚1

(1.宁夏师范学院数学与计算机科学学院,宁夏固原756000)

(2.北京师范大学数学科学学院,北京100875)

本文研究了多重时滞富营养化生态模型的稳定性与分支问题.利用特征值方法,分别研究了具有单时滞和双时滞模型的线性稳定性.发现当模型中的时滞经过一系列临界值时,模型在平衡点附近经历了Hopf分支和Hopf-zero分支,并给出Hopf分支和Hopf-zero分支存在的充分条件.最后数值模拟验证了理论结果.

双时滞;稳定性;Hopf分支;Hopf-zero分支

1　引言

水体的富营养化可以导致一系列严重问题,比如生态完整性遭到破坏.它的特点是藻类大量繁殖,其它水生物大量减少.浙江省温州市泽雅水库处于副热带地区,由于藻类大量繁殖造成过滤系统堵塞,导致数以百万计的人的饮用水危机.水体富营养化的去除主要有物理化学和生物处理两种方法[1].为了更好的控制水体富营养化等污染状态出现,有必要对水体中生态系统进行研究[2-4].泽雅水库富营养化过程与水体中的藻类数量密切相关,同时也与水体中的滤食性鱼类(如鲢鱼和鳙鱼)相关.为了能更好的应用生物学原理控制泽雅水库的富营养化,基于文献[5],于恒国,赵敏等在文献[6]中考虑了两种滤食性鱼类鲢鱼和鳙鱼,提出了一个新的模型如下

其中x(t)表示t时刻藻类的数量,y(t)和z(t)分别表示t时刻滤食性鱼类鲢鱼和鳙鱼的数量,r表示藻类的内禀增长率,αi(i=1,2)分别表示鲢鱼和鳙鱼的投放率,ei(i=1,2)分别表示鲢鱼和鳙鱼转化为消费者的比率,k表示x(t)的承受力,δi(i=1,2)分别表示鲢鱼和鳙鱼的饱和常数,ρi(i=1,2)分别表示鲢鱼和鳙鱼的相互影响因子,mi(i=1,2)分别表示鲢鱼和鳙鱼的死亡率,γ表示鲢鱼的相对优势,τ、τ1和τ2是正时滞.

在文献[6]中,作者给出了方程(1.1)的平衡点稳定的充分条件,并用数值模拟的方法对方程(1.1)进行了详细的研究.本文中取τ1=τ2=σ,从稳定性与分支的角度研究系统(1.1),对该系统的平衡点稳定性、Hopf分支和Hopf-zero分支的存在性进行分析．

2　平衡点的稳定性和分支的存在性

显然,S0=(0,0,0)和S1=(k,0,0)始终是系统(1.1)的平衡点.平衡点S0表示水体中藻类、鲢鱼和鳙鱼都不存在.平衡点S1表示水体中藻类存在,而鲢鱼和鳙鱼不存在.在一定条件下,系统(1.1)还有其它平衡点.

(1)当γe1α1＞0,kγe1α1＞m1(k+δ1)时,系统(1.1)存在平衡点S2=(x2,y2,0),其中

此时水体中只有藻类和鲢鱼存在,鳙鱼不存在.

(2)当e2α2＞m2,ke2α2＞m2(k+δ2)时,系统(1.1)存在平衡点S3=(x3,0,z3),其中

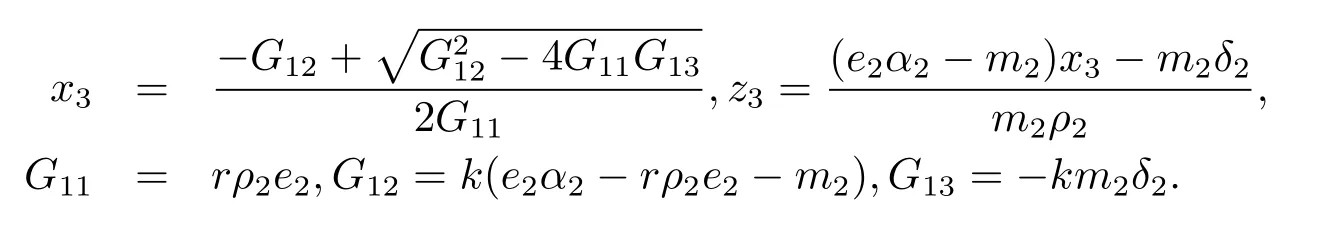
此时水体中只有藻类和鳙鱼存在,鲢鱼不存在.

(3)当

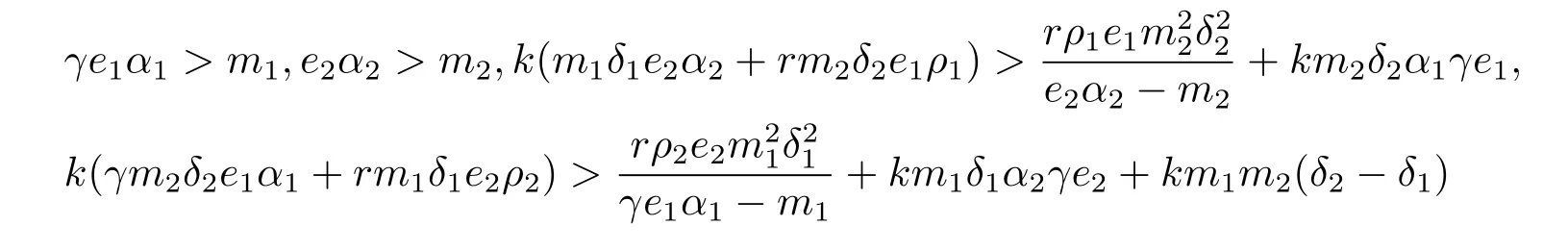
时,系统(1.1)存在平衡点S4=(x4,y4,z4),其中

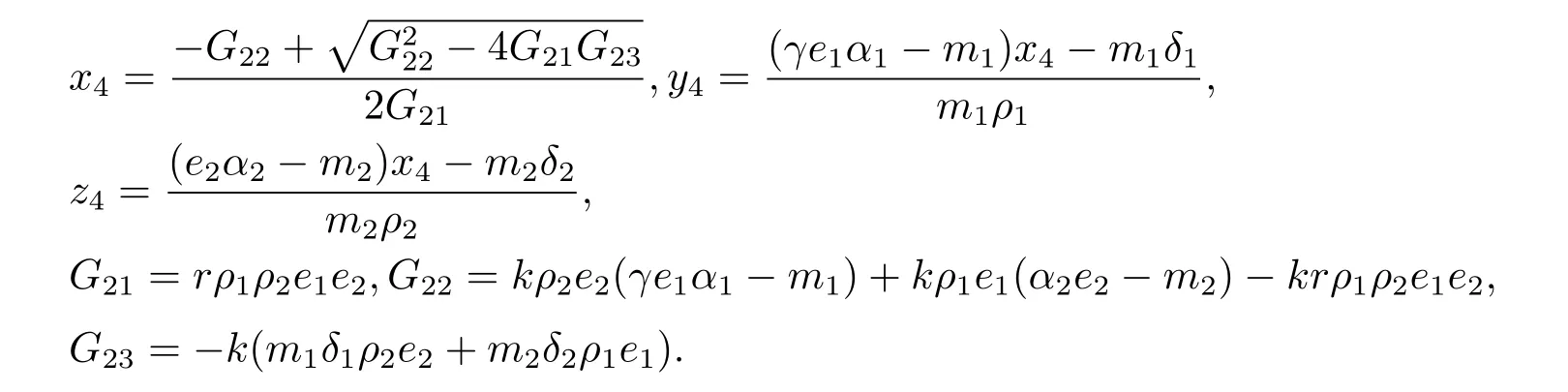
此时水体中藻类同滤食性鱼类鲢鱼和鳙鱼共存.

不失一般性,本文只讨论平衡点S4.系统(1.1)在平衡点S4处的特征方程为

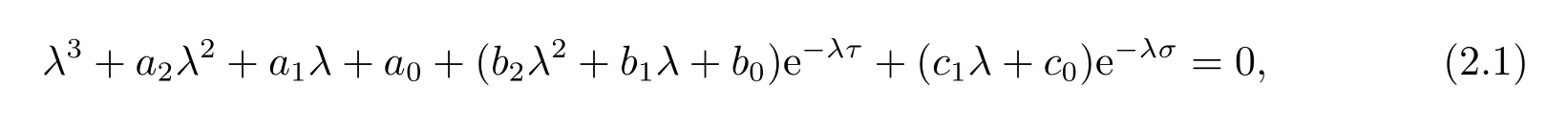
其中

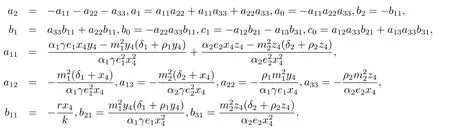
注特征方程(2.1)是一个超越方程,研究起来比较复杂.据作者了解,目前还没有研究类似于方程(2.1)的文献.

2.1τ=0,σ=0的情形

此时方程(2.1)变为

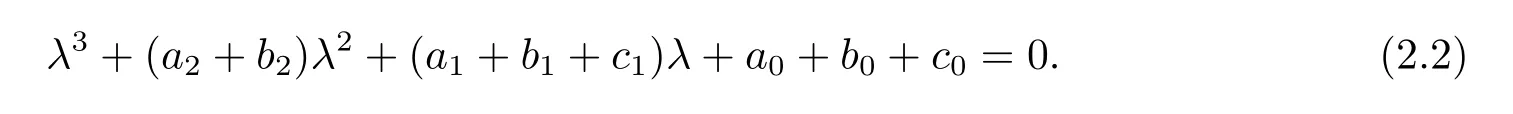
根据微分方程的定性理论以及Hurwitz判据[7],可得如下引理.

引理2.1(i)当a0+b0+c0=0时,λ=0是方程(2.2)的根;当a0+b0+c0=0, a1+b1+c1＞0,且a2+b2＞0时,方程(2.2)有一个零根和两个具有负实部的根.此时,系统(1.1)经历了不动点分支;

(ii)当a2+b2＞0,a0+b0+c0＞0,(a2+b2)(a1+b1+c1)＞a0+b0+c0时,方程(2.2)的所有根具有负实部.

作如下假设

(H1)a2+b2＞0,a0+b0+c0＞0,(a2+b2)(a1+b1+c1)＞a0+b0+c0.

此时方程(2.1)变为

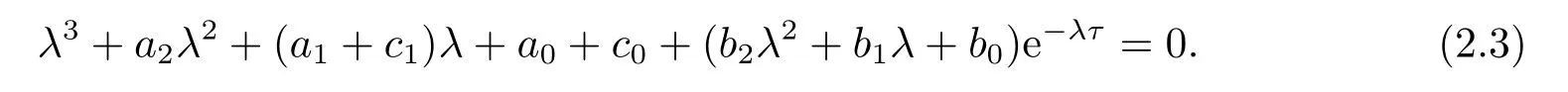
显然,iβ(β＞0)是方程(2.3)的根当且仅当β满足

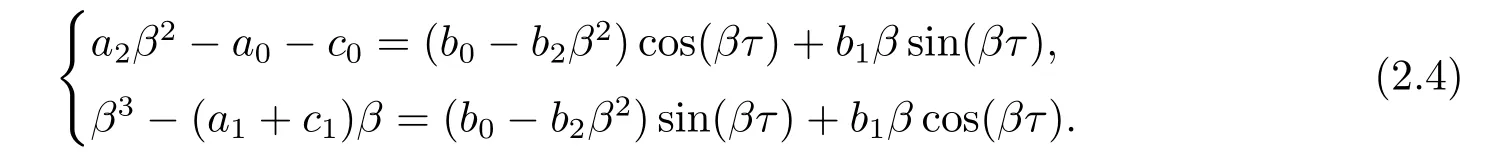
平方相加,并令ξ=β2可得

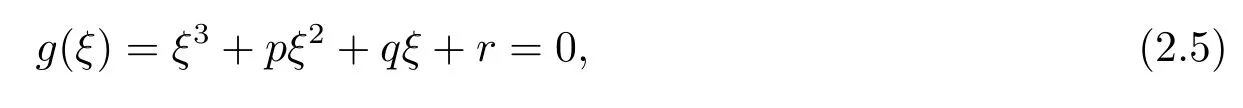
其中

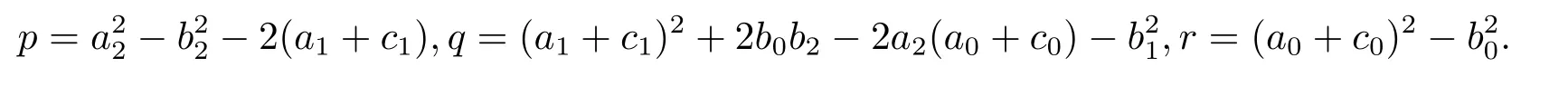
引理2.2(i)当r＜0时,方程(2.5)至少有一个正实根;

(ii)当r≥0且p2≤3q时,方程(2.5)没有正实根;

(iii)当r≥0且p2＞3q时,方程(2.5)有正实根的充要条件是z∗=＞0且 g(z∗)≤0,其中∆=p2-3q.

(iii)如果r≥0且∆＞0,3ξ2+2pξ+q=0有两个实根z∗=和ξ∗=

充分性因为g＇＇(z∗)=＜0,即z∗是g(ξ)的极小值点,ξ∗是g(ξ)的极大值点.又g(ξ)=∞,所以当z∗＞0且g(z∗)≤0时,方程(2.5)有正实根.

必要性否则,假设z∗≤0或者z∗＞0且g(z∗)＞0.因为函数g(ξ)在[z∗,∞)上单调增加,且g(0)=r＞0,所以当z∗≤0时方程(2.5)无正实根.矛盾.因为ξ∗是g(ξ)的极大值点,所以g(z∗)＜g(ξ∗),且g(0)=r＞0,所以当z∗＞0且g(z∗)＞0时方程(2.5)无正实根.矛盾.引理2.2得证.

作如下假设

(H2)r≥0,p2≤3q;

(H3)r＜0;

(H4)r≥0,p2＞3q,z∗=＞0且g(z∗)≤0.

不失一般性,假设方程(2.5)有三个正实根ξ1,ξ2和ξ3.所以方程(2.3)有三个正实根(k=1,2,3).记

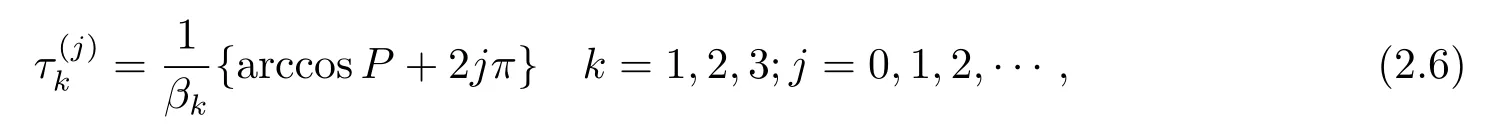
其中

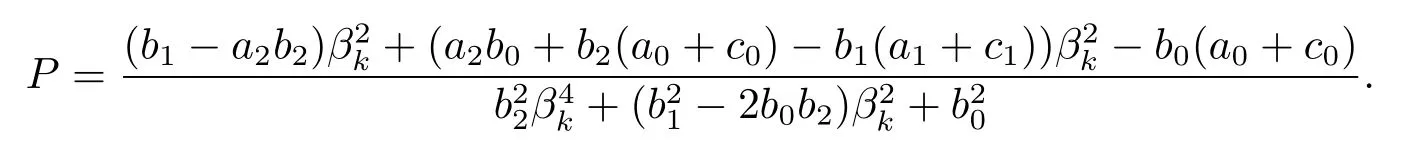
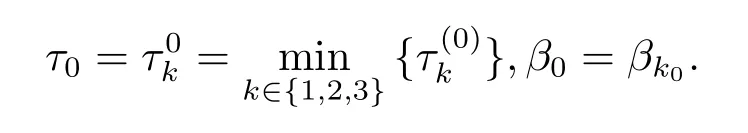
引理2.3[8]设

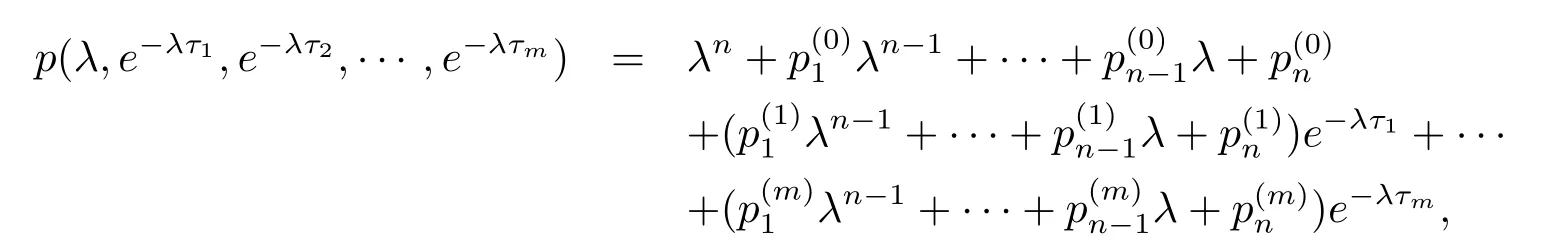
其中τi≥0(i=1,2,···,m),(i=0,1,···,m;j=1,2,···,n)是常数,则当τ1,τ2,···,τm变化时,p(λ,e-λτ1,e-λτ2,···,e-λτm)位于右半平面的零点重数之和只有当虚轴上出现零点或有零点穿过虚轴时才发生变化.

由引理2.2和引理2.3可得下面引理.

引理2.4假设(H1)成立.

(i)如果(H2)成立,则当τ≥0时,方程(2.3)的根都具有负实部;

由隐函数定理,存在ε0＞0,使得当|τ-|＜ε0时,方程(2.3)有一对虚根λ(τ)= α(τ)±iβ(τ),且满足α()=0,β()=βk(k=1,2,3).

证把λ(τ)代入方程(2.3)并对τ求导可得

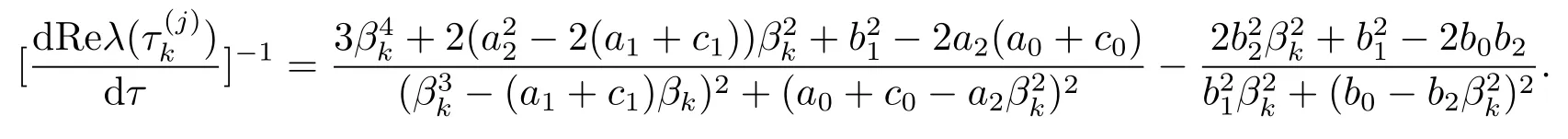
由(2.4)式可得

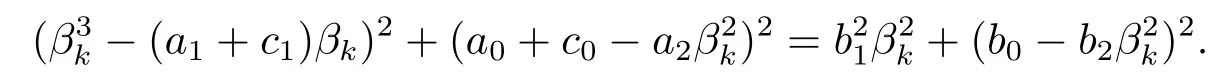
因此

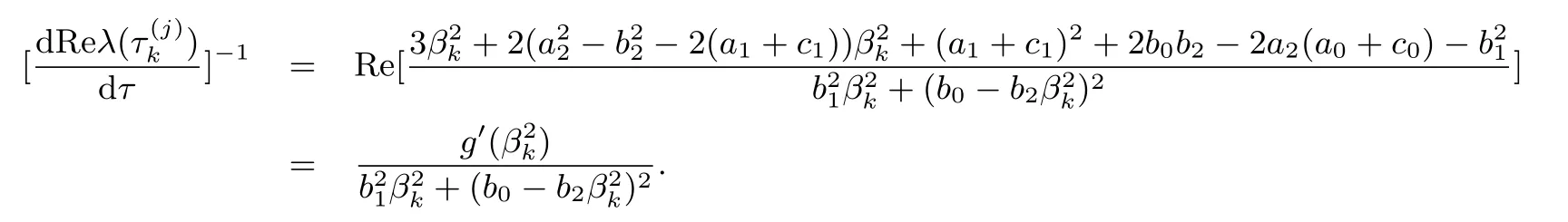
定理2.1假设(H1)成立.

(i)如果(H2)成立,则当τ≥0时,系统(1.1)的平衡点S4是局部渐近稳定的;

(ii)如果(H3)或者(H4)成立,则当τ∈[0,τ0)时,系统(1.1)的平衡点S4是局部渐近稳定的.而且如果0,则当τ=时,系统(1.1)在平衡点S4处经历了Hopf分支.

证由引理2.3可得(i)和(ii)的前半部分正确.由文献[9]中关于泛函微分方程的Hopf分支定理可得(ii)的后半部分正确.定理2.1得证.

引理2.6如果a0+b0+c0=0,a1+b1+c1＞0,a2+b2＞0,并且(H4)成立,则当τ∈[0,τ0)时,方程(2.3)除了有一个零根外,其余根都具有负实部.

证因为a0+b0+c0=0,所以0是方程(2.3)的根.由引理2.4可知,方程(2.3)没有纯虚根.

用反证法.令a0+b0+c0=a,假设存在τ∗∈(0,τ0)使得方程(2.3)有实部为正的根,记为λ0=υ0+iζ0,设λ(a,τ)=υ(a,τ)+iζ(a,τ)是方程(2.3)的根,且满足υ(a=0,τ∗)= υ0＞0,ζ(a=0,τ∗)=ζ0.因为υ(a,τ)关于a连续,则存在κ1＞0,当a∈(0,κ1)时, υ(a,τ∗)＞0.又τ0(a)=τ0,所以对0＜γ0≤τ0-τ∗,存在κ2＞0,当a∈(0,κ2)时,使得|τ0(a)-τ0|＜γ0,进而可得τ∗∈(0,τ0(a)).取κ=minκ1,κ2,则当a∈(0,κ)时,υ(a,τ∗)＞0且τ∗∈(0,τ0(a)).又由引理2.4,当a∈(0,κ)方程(2.3)的根都具有负实部.这是一个矛盾.引理2.6得证.

定理2.2如果a0+b0+c0=0,a1+b1+c1＞0,a2+b2＞0,并且(H4)成立,则当τ=τ0时,方程(2.3)除了有一个零根和一对纯虚根±iβ0外,其余根都具有负实部.此时系统(1.1)在平衡点S4处经历了Hopf-zero分支.

证因为a0+b0+c0=0,所以0是方程(2.3)的根.由引理2.4可知±iβ0也是方程(2.3)根.假设当τ=τ0时,方程(2.3)有一个根具有正实部,记为λ0=υ0+iζ0.λ(τ)=υ(τ)+iζ(τ)是方程(2.3)的根,且满足υ(τ0)=υ0＞0,ζ(τ0)=ζ0.因此当τ→时,方程(2.3)有具有正实部的根,这与引理2.6矛盾.定理2.2得证.

本小节中,固定τ,以σ为参数,且τ取值于使方程(2.3)的根都具有负实部的区间.设iω(ω＞0)是方程(2.1)的根,则可得

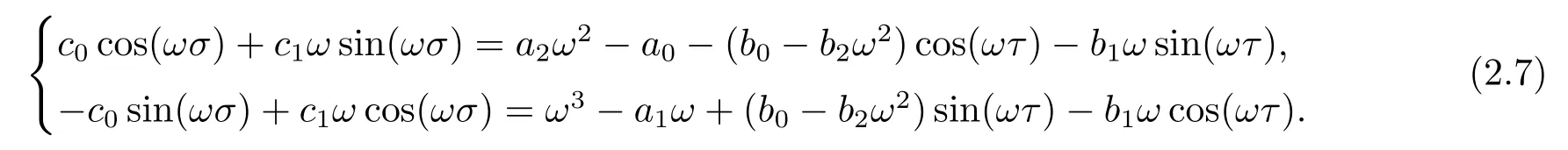
把(2.7)式中两个方程平方相加可得

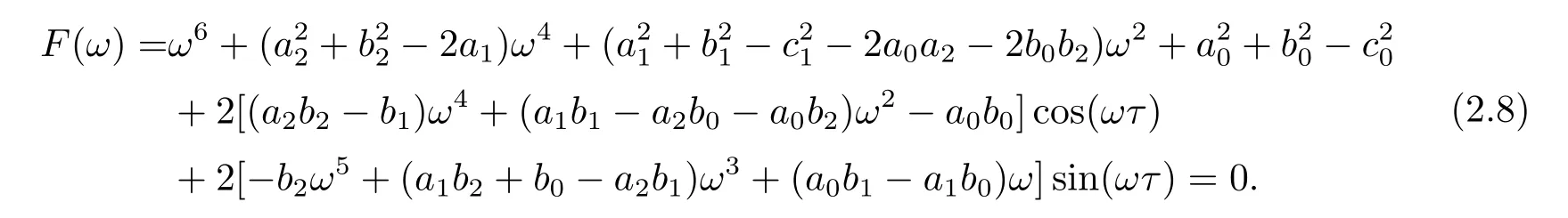
假设方程(2.8)有有限个正根ω1,ω2,···,ωs.则与每个ωk(k=1,2,···,s)相对应的为

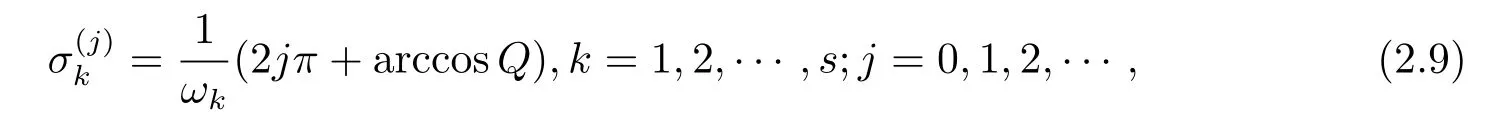
其中

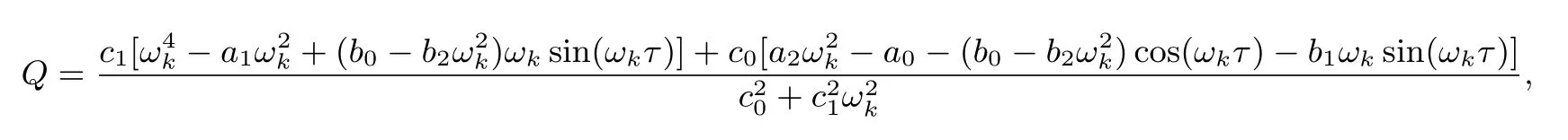
则(ωk,)是方程(2.7)的根.由此可得如下引理2.7.

定义

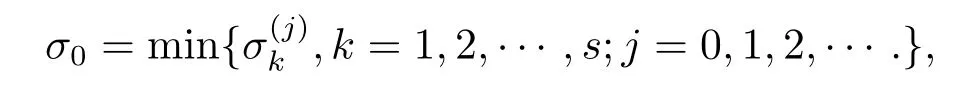
并记与之相对应的ωj为ω0.假设λ(σ)=α(σ)+iω(σ)是特征方程(2.1)在σ=附近的根,且满足α(σ0)=0,ω(σ0)=ω0.

其中

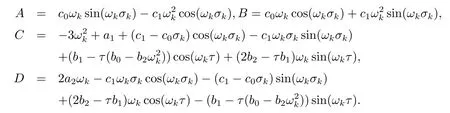
证方程(2.1)两端同时关于σ求导可得

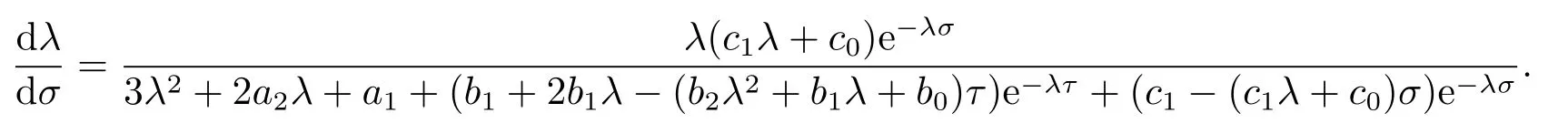
通过直接而繁琐的计算可得

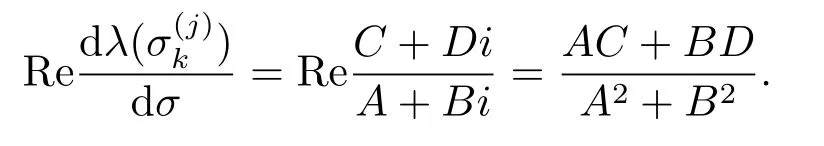
由本文引理2.1至引理2.8和文献[9]中第11章的定理1.1,可以得到下面关于系统(1.1)的平衡点的稳定性与Hopf分支的存在性定理.

定理2.3假设(H1)成立,

(i)如果(H2)成立且F(ω)没有正根,则当σ≥0时,系统(1.1)的平衡点S4是局部渐近稳定的;如果(H2)成立且F(ω)有正根,则当σ∈[0,σ0)时,系统(1.1)的平衡点S4是局部渐近稳定的;在后一种情况,如果AC+BD0,则当σ=(k=1,2,···,s;j=0,1,2,···)时,系统(1.1)在平衡点S4处经历了Hopf分支.

(ii)如果(H3)或(H4)成立,τ∈[0,τ0),且F(ω)没有正根,则当σ≥0时,系统(1.1)的平衡点S4是局部渐近稳定的;如果(H3)或(H4)成立,τ∈[0,τ0),且F(ω)有正根,则当σ∈[0,σ0)时,系统(1.1)的平衡点S4是局部渐近稳定的;在后一种情况,如果AC+BD0,则当σ=(k=1,2,···,s;j=0,1,2,···)时,系统(1.1)在平衡点S4处经历了Hopf分支.

综合上面的讨论可得关于系统(1.1)的Hopf-zero分支的存在定理.

定理2.4假设a0+b0+c0=0,a1+b1+c1＞0,a2+b2＞0,且方程(2.8)至少有一个正实根ωk(k=1,2,···,s),

(i)如果(H2)成立,则当σ=σ0时,系统(1.1)在平衡点S4附近经历了Hopf-zero分支;

(ii)如果(H4)成立,τ∈[0,τ0),则当σ=σ0时,系统(1.1)在平衡点S4附近经历了Hopf-zero分支.

证因为a0+b0+c0=0,所以0是方程(2.1)的根.由引理2.7可得,±iσ0是方程(2.1)的一对纯虚根.类似于定理2.2的证明可得,当σ=σ0时,方程(2.1)除了一个零根和一对纯虚根±iσ0外,其余根均具有负实部,即系统(1.1)在平衡点S4附近经历了Hopf-zero分支.定理2.4得证.

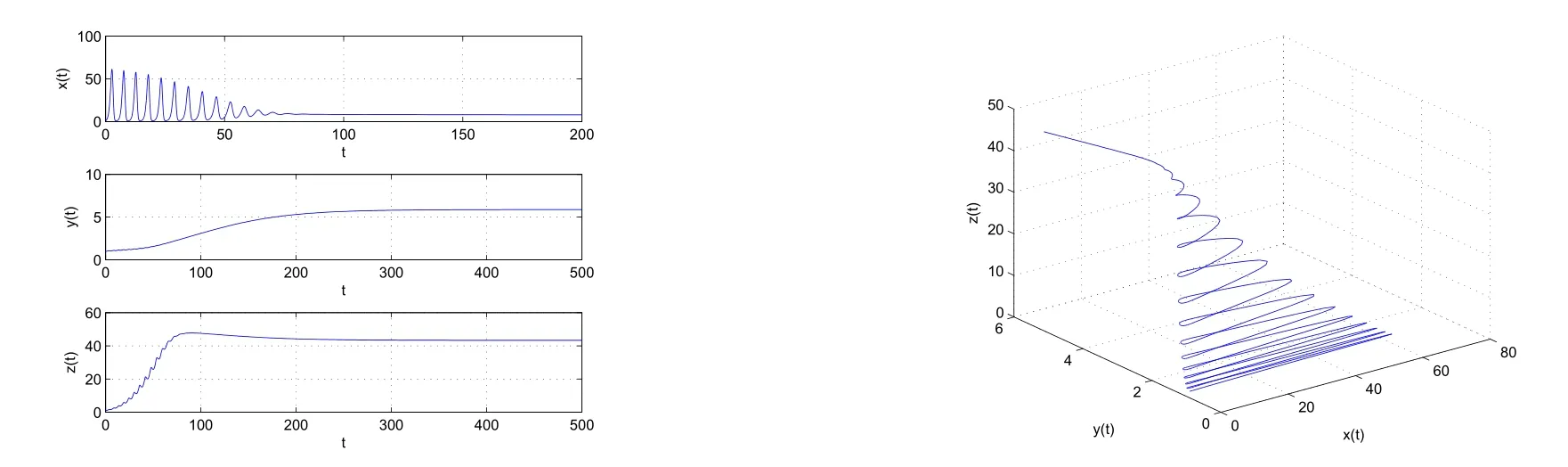
图1:当τ=1.01时,系统(1.1)的平衡点S4局部渐近稳定.

图2:当τ=1.4时,系统(1.1)在平衡点S4附近经历了Hopf分支.

3　数值模拟

为了研究具多重时滞水体富营养化生态模型的复杂动力学行为,本文应用微分方程的稳定性和分支理论得到了平衡点的稳定性区域和周期解存在的充分条件.为了说明理论结果的正确性,下面进行数值模拟.

参照文献[6]中的数据,取r1=2.1,k=20,e1=0.45,e2=0.5,a1=0.8,a2= 0.6,β=0.35,b1=0.25,b2=2.5,c1=0.25,c2=0.55,m1=m2=1.通过计算知(H1)和(H3)满足,g(ξ)有一个正根ξ1≈1.18,所以β1≈1.0861,g＇()＞0.由(2.6)式和引理2.5可得

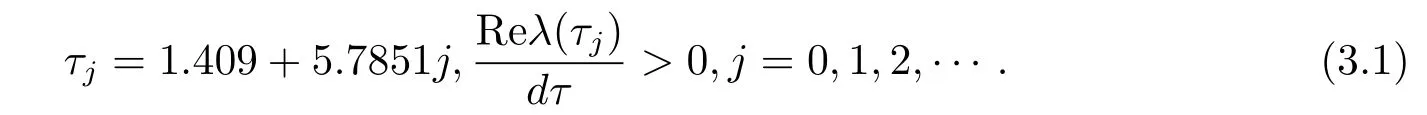
所以计算可得τ0=1.409.因此由定理2.1和(3.1)式可得如下结论.

结论3.1假设τj(j=0,1,2,···)如(3.1)式定义,

(i)当τ∈[0,τ0)时,系统(1.1)的平衡点S4是局部渐近稳定的(如图1所示);

(ii)当τ=τj(j=0,1,2,···)时,系统(1.1)在平衡点S4处经历了Hopf分支(如图2所示).

4　结论

本文研究了基于浙江省温州市泽雅水库的双时滞富营养化生态模型.通过对系统线性化方程的特征方程根的分布分析入手,得出了系统的线性稳定性区域,当时滞经历一系列临界值时,系统经历了Hopf分支和Hopf-zero分支.本文研究表明,时滞在系统(1.1)的复杂动力学行为中起了重要作用,时滞可以使得藻类和滤食性鱼类(鲢鱼和鳙鱼)在稳定状态下共存.即时滞对生态种群的稳定性有积极影响.

[1]Lee C G,Fletcher T D,Sun G Z.Nitrogen removel in constructed wetland systems[J].Eng.Life Sci.,2009,9:11-22.

[2]Shukla J B,Misra A K,Chandra P.Mathematical modeling and analysis of the depletion of dissolved oxygen in eutrophied water bodies affected by organic pollutants[J].Nonl.Anal.:Real World Appl., 2008,9:1851-1865.

[3]Alvarez L J,Fernandez F J,Munoz R.Mathematical analysis of a three-dimensional eutrophication model[J].J.Math.Anal.Appl.,2009,349:135-155.

[4]张艳红.三种群的竞争系统全局解的一致有界性[J].数学杂志,2012,32(6):1129-1135.

[5]Xiu P,Liu J.Practical success of biomanipulation using filter-feedings fish to control syanobacteria blooms a synthesis of decades of research and application in a subtropuical hypertrophic lake[J]. Sci.World,2001,1:337-356.

[6]Yu H G,Zhao M,Agarwal R P.Stability and dynamics analysis of time delayed eutrophication ecological model based upon the Zeya reservoir[J].Math.Comput.Simul.,2014,97:53-67.

[7]马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.

[8]Ruan S,Wei J.On the zeros of transcendental functions to stability of delay differential equations with two delays[J].Dyn.Contin.Discrete Impuls.Syst.A Math.Anal.,2003,10:863-874.

[9]Hale J K,Lunel S V.Introduction to functional differential equation[M].New York:Springer-Verlag, 1993.

2010 MR Subject Classification:34C23

STABILITY AND BIFURCATION ANALYSIS OF MULTIPLE TIME DELAY EUTROPHICATION ECOLOGICAL MODEL

YANG Ji-hua1,2,LIU Mei1
(1.School of Mathematics and Computer Science,Ningxia Normal University,Guyuan 756000,China)
(2.School of Mathematical Science,Beijing Normal University,Beijing 100875,China)

In this paper,the stability and bifurcation problem of eutrophication ecological model with two time delays is studied.By using the eigenvalue method,we study the linear stabilities with one delay and two delays,respectively.It is found that Hopf bifurcations and Hopf-zero bifurcations exist at the equilibriums when the delays pass through a sequence of critical values.The sufficient conditions of the existence of Hopf bifurcation and Hopf-zero Bifurcation are obtained.In the end,some numerical simulations are carried out for supporting the analytic results.

two time delays;stability;Hopf bifurcation;Hopf-zero bifurcation

MR(2010)主题分类号:34C23O175

A

0255-7797(2016)06-1222-09

∗2015-02-10接收日期:2015-07-06

国家自然科学基金资助(11361046);宁夏自然科学基金(NZ13213);宁夏高等学校科研项目(宁教高[2014]222号(17);宁教高[2014]222号(16)).

杨纪华(1983-),男,河南周口,讲师,主要研究方向:微分方程的稳定性与分支理论.