用Cesàro方法计算等时摆及摆绳等分点的运动轨迹

刘钦记，彭建华

(1.深圳大学光电工程学院，广东深圳518060； 2.深圳大学物理科学与技术学院，广东深圳518060)



用Cesàro方法计算等时摆及摆绳等分点的运动轨迹

刘钦记1，彭建华2

(1.深圳大学光电工程学院，广东深圳518060； 2.深圳大学物理科学与技术学院，广东深圳518060)

基于等时性和利用微分几何中的Cesàro方法，解析地确定等时摆球的运动轨迹以及限制摆绳运动的曲线，同时还获得摆绳上不同等分点运动曲线的一般解析式. 所得结果将有助于全面认识此等时摆系统的运动学规律.

等时性； 旋轮线； 微分几何； Cesàro方法

1 引 言

1656年，惠更斯将单摆运动的等时性原理引入时钟设计发明了著名的摆钟.实际上，他在研究摆钟的过程中发现：伽利略发现的单摆等时性现象，即摆的运动周期与摆动的幅度无关，只有在摆角较小的范围内存在；而当摆角范围大了，摆动则不严格等时.惠更斯进一步研究得到结论：若能使摆的轨迹呈旋轮线，在可摆动的范围内，无论摆角多大，摆的运动都具有等时性.惠更斯的摆线理论不仅为当时设计和制作摆钟提供了重要的依据，也为后来在科学和技术发展和应用方面都产生了积极的作用[1，2].在已报道的有关等时性的研究中，许多作者利用不同的方法,主要集中研究了等时条件下摆球的运动学方程和摆绳被约束的曲线方程[3,4].实际上，除了这两条曲线方程外，摆绳上其他动点的运动学方程：如摆动过程中，受到限制的摆绳中点；或中点至摆球间的系列点，所有这些点的运动学方程的解析表达式为何？目前尚未见报道.若能确定出这些点的运动学方程，对于全面研究此系统的运动规律是有意义的.与其他作者研究方法不同的是，本文从物理上物体做简谐运动的物理条件出发，利用微分几何中的Cesàro方法[6]，解析研究在等时条件下，摆绳各等分动点对应的曲线方程，进而也可求出摆球运动曲线和约束摆绳的曲线.

2 等时性运动的重要条件

单摆在大幅度摆动的过程中周期不是常量而只能用椭圆积分表示[5]，但可采用某种补偿的方式，以实现等时的目标.具体的设计方案如图1所示，在摆绳的两侧对称加装具有某类曲线状的限制片，限制片的作用是：摆球在摆动过程中，摆绳贴到限制片上相当于绳的“悬挂点”迁移，原长为l0的绳摆动部分的长度逐渐变短，直至达最短；而绳脱离限制片后，摆动部分的绳又逐渐变长，在平衡点处恢复至原长l0.加装的简单限制器唯一限制的参量是摆绳的长度.一个自然的问题是，限制片应采用何种形状才能获得等时的效果.

我们将图1简化为图2，曲线C1为限制片的形状，曲线C为摆球的运动轨迹.通过可摆动部分的绳长即C上各点的曲率半径，一一建立曲线C1和C上点与点的对应关联.在自然坐标系下，根据牛顿第二定律建立摆球沿轨线切向的动力学方程，具体为

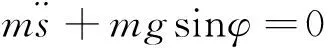
(1)

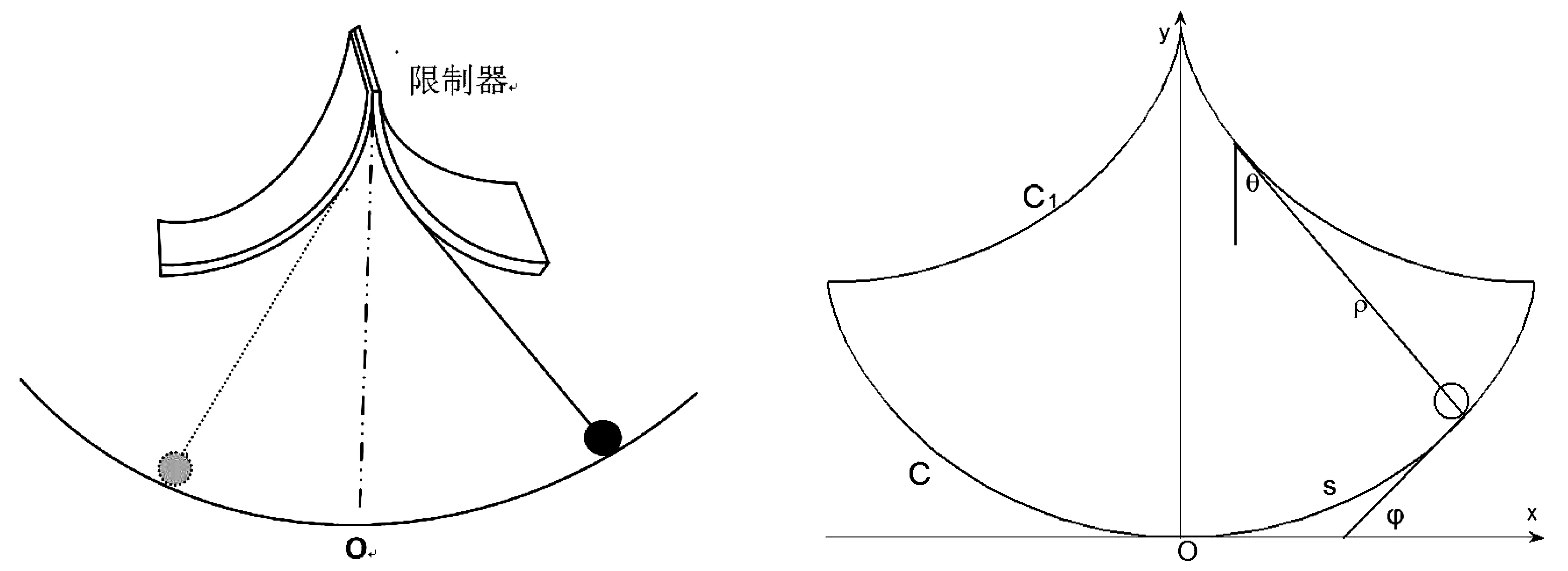
图1 图2

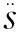
s=Ksinφ,

(2)

其中K为待定常数，(1)可转化为

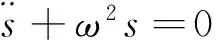
(3)

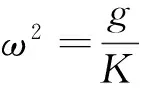
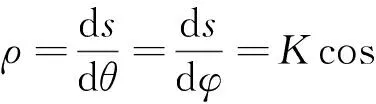
(4)

当φ=0时, 对应摆线处于竖直位置，恢复为原长的情况, 有

ρ(0)=K=l0，

也就是

运动为等时.不难看出(2)或(4)式是等时性成立的重要条件.进一步可利用常规方法导出摆球运动方程和限制器的曲线方程.在切点附近

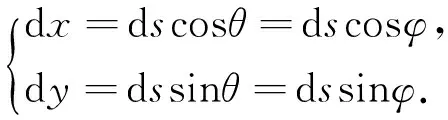
(5)

联立式(4)和式(5)，并积分得

(6)

若取r=K/4和Φ=2φ, 式(6)正是旋轮线的参数方程.注意到本模型中伴随曲线C1上的点(x1,y1)与原曲线C上的对应点(x,y)有如下关系

(7)

联立式(6)和式(7),可得C1的参数方程

(8)

这就是在等时条件下对限制片形状的要求.式(6)和式(8)的结果是我们熟知的旋轮线.但是仅利用上述常规方法是难以求出摆绳不同等分点的运动轨迹的，而利用微分几何中的Cesàro方法则是一个很好的方法，它仅需利用等时性的重要条件——(4)式，即可求出摆球运动的参数方程、约束摆绳的参数方程，摆绳不同等分点的运动轨迹.

2 用Cesàro方法计算摆绳不同等分点运动轨迹

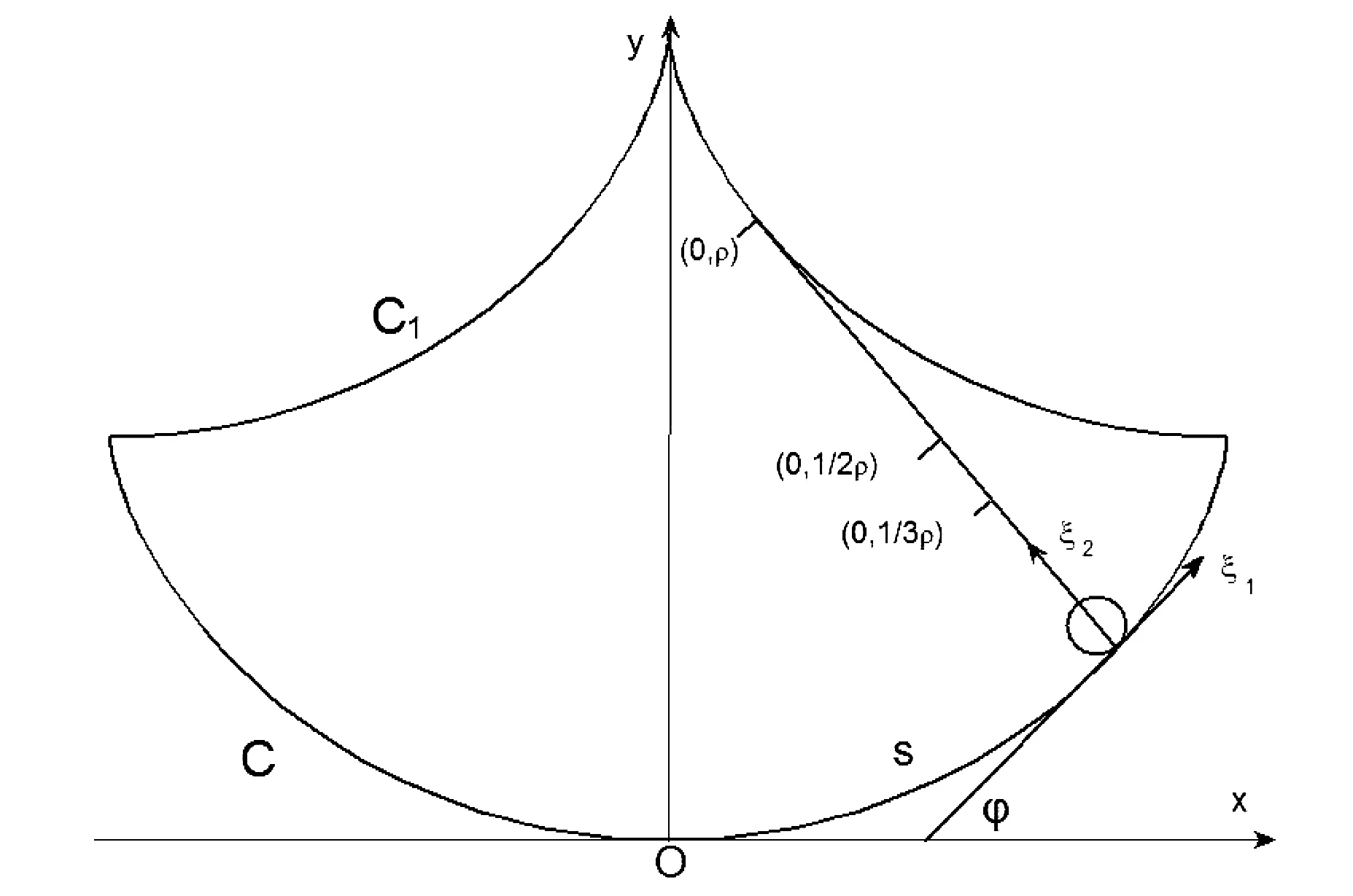
图3 等分曲率半径的图示

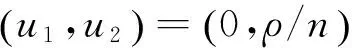
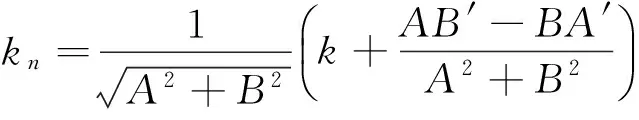
(9)

其中

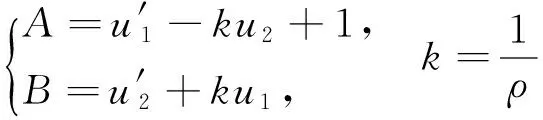
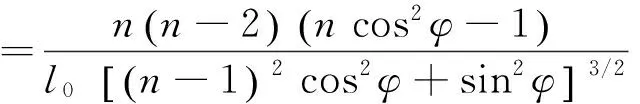
(10)

曲率半径为

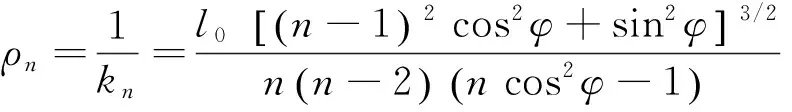
(11)

设伴随曲线相对于绝对坐标系的切角为β，其变化率为[6]

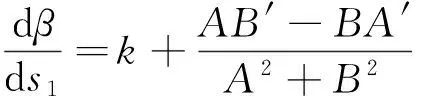
(12)

由此得β与φ的关系为

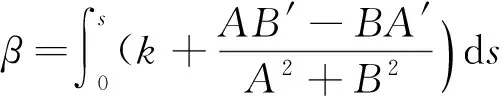
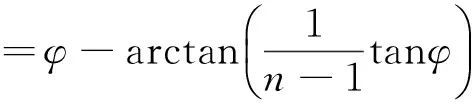
(13)

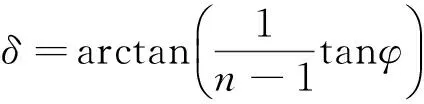
(14)

和

(15)

故

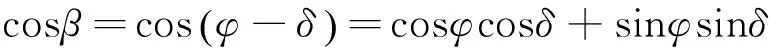
(16)

和

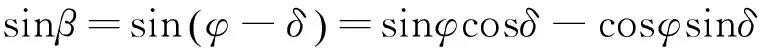
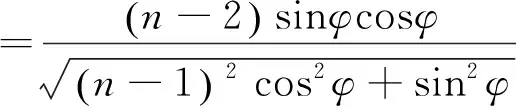
(17)

在与C曲线对应的伴随曲线的切点附近，有

(18)

联立式(11)，(13)，(16)，(17), 并分别积分得伴随曲线的参数方程为

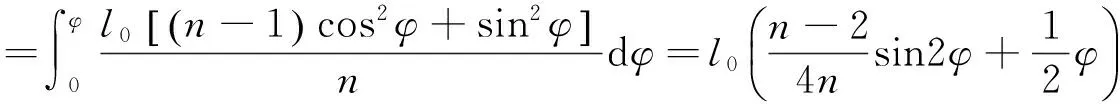
(19)

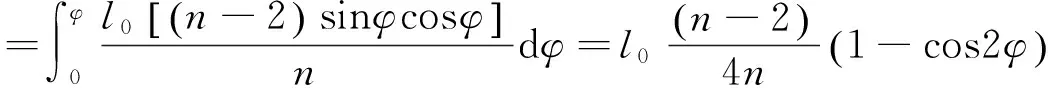
(20)

整理式(19)和(20)，得

(21)

当n=1时，由(21)得

(22)

这显然是限制器的曲线形状，与式(8)是吻合的.

当n→∞时，由(21)得

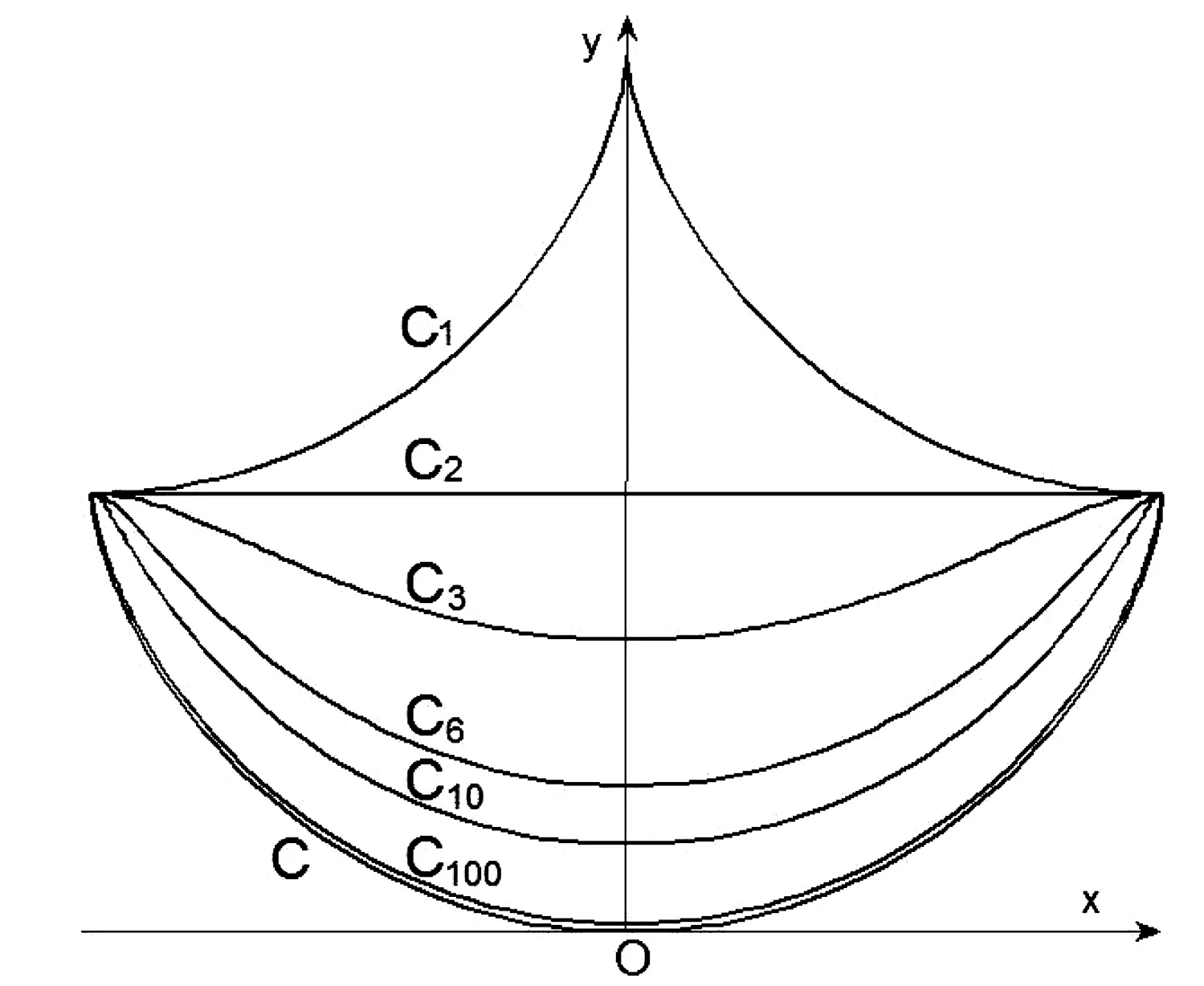
图4 对应曲线C的伴随曲线族部分成员

(23)

这是摆球的运动轨线，与式(6)也是吻合的.

另外在n∈[1,∞)内取不同的数时可以得到不同等分点的轨迹，如取n=2，可由式(21)得

(24)

摆绳l(t)中点的运动轨线；

取n=3，由(21)得

(25)

利用Matlab软件绘制n=1,2,3,6,10,100情况下的几条伴随曲线[7].如图4所示.

上述所讨论的结果也可做进一步推广,如可应用到小滑块沿对称的凹型滑道往复运动的问题中，欲使滑块的运动具有等时性，类似上述操作过程,可分别确定小滑块运动轨道等规律，本文不再做讨论.

3 结 论

利用等时性条件(2)或(4)，我们通过Cesàro方法不仅给出等时摆轨线和限制器曲线形状的又一种解法，同时还解析求出摆绳等分点的运动轨迹.我们的这一工作是将微分几何中Cesàro方法应用于物理学中的范例.所获得的结果也丰富了关于等时问题的研究.

[1] 刘延柱.趣味振动力学[M].北京：高等教育出版社, 2012.

[2] 武际可.力学引领下改变人类生活的三项发明[J]. 科技导报，2015，33：109.

[3] 舒幼生.趣味滚轮线[J]. 科学,2000,05:58-60.

[4] 陈钢. 惠更斯摆及严格等时性[J].大学物理,2003,22(11):15-17.

[5] 胡绍宗. 椭圆积分的计算及其应用[J].大学数学, 2013,29(1):111- 115.

[6] 佐佐木重夫, 微分几何学[M]. 苏步青译.上海：上海科学技术出版社, 1963.

[7] 段俊生,安建业,徐立. Matlab 曲面绘制中的挖补方法[J].大学数学, 2006,22(4):36-39.

Calculate the Trajectory of Moving Points in the Isochronal Pendulum Using Cesàro’s Method

LIUQin-ji1,PENGJian-hua2

(1.College of Optoelectronic Engineering , Shenzhen University , Shenzhen Guangdong 518060, China;2. College of Physics and Technology , Shenzhen University , Shenzhen Guangdong 518060, China)

Using Cesàro’s method in differential geometry, the trajectory of an isochronous pendulum ball and the shape of the limiter are determined analytically. General analytical expressions of the trajectories of the swinging rope at equal division points are further derived.

isochronous ; cycloid ; differential geometry ; Cesàro’s method

2016-03-10； [修改日期]2016-04-04

国家自然科学基金(11205104；70571053)

刘钦记(1994-),男, 2013级本科生,光电信息科学与工程专业.Email:2013800345@email.szu.edu.cn

O29

A

1672-1454(2016)05-0025-05