三角形区域上复合边值问题探讨

胡 洁，刘 华

（天津职业技术师范大学理学院，天津 300222）

三角形区域上复合边值问题探讨

胡 洁，刘 华

（天津职业技术师范大学理学院，天津 300222）

针对三角形区域上的复合边值问题，采用问题转化求解的办法，研究该问题的解析解。利用Schwarz-Christoffel公式给出圆域到三角形区域的共形映射，依据椭圆函数的相关理论推导出三角形区域到圆域的逆映射；将三角形区域上的复合边值问题转化为圆域上的复合边值问题，进一步通过消去法把复合边值问题化为带间断系数的Hilbert边值问题，通过解析延拓化为带间断系数的联结问题，得出三角区域上复合边值问题的解析解。

Schwarz-Christoffel公式；椭圆函数；Plemelj公式；复合边值问题

解析函数的边值问题是复变函数论中一个不可或缺的分支，与很多实际问题密切相关，并广泛应用于物理学和工程技术等众多领域。1962年路见可[1-2]首次将联结问题（简称R问题）和Hilbert问题（简称H问题）结合，进而提出复合边值问题（简称RH问题）同时给出解析解。之后，研究人员进一步讨论各类边值问题。2002年，张霞和李星[3]研究了非正则型解析函数的复合边值问题；Guo[4]在2012年对无穷边界上的边值问题进行了深入研究。当然，很多固体力学、断裂理论和平面弹性的实际问题，都可以转化为边值问题或奇异积分方程，而后者又与边值问题有密切联系，这类应用也引起学者们的重视。路见可和李星[5-6]陆续采用复分析来解决物理中的弹性力学问题。之后，李星[7]推广了单裂缝的情况，利用Hilbert奇异积分方程得到了数值解；2001年他又讨论了复分析在力学中的应用[8-9]。Begehr教授[10]也对复分析及其在力学中的应用进行了研究。近几年，针对平面弹性的稳定性及相关特性，杜金元[11-12]也进行了进一步的研究推导。

本文研究的复合边值问题与以往有所区别，并没有把区域边界只限定在Lyapunov曲线上，而是考虑在更为一般的多角形域上解决复合边值问题。通过共形映射理论[13-14]“消去法”将其化为经典区域上带间断系数的Hilbert问题之后再求解，巧妙地处理特殊点的奇异性，进而得到完善的解析解。

1 RH复合边值问题的提出与转化

1.1 复合边值问题的提出

设复平面上的正三角形边界曲线为L（取逆时针方向为正），内部区域记为G。在G中有一条光滑封闭曲线Γ（取顺时针方向为正），Γ内部围成的区域记为D-，Γ和L围成的部分记为D+，如图1所示。

三角形区域上的复合边值问题（记为RH问题）为：求G中一个分区全纯函数Φ（z），该函数连续到边界L上，且满足以下边值条件。

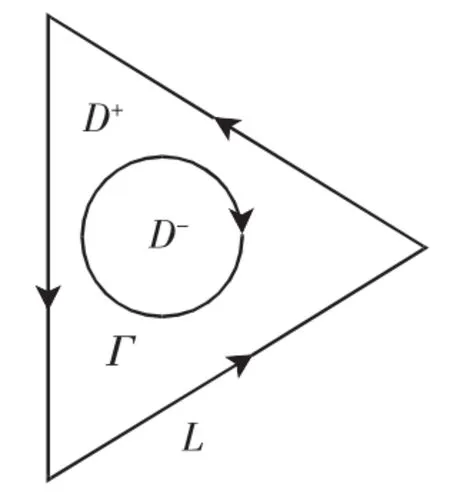
图1 三角形区域

（1）在跳跃曲线Γ上（Φ（z）在D+和D-内全纯、在L上及Γ的正负侧均有极限值）满足

式中：G（τ）、g（τ）在跳跃曲线上满足Hölder条件，且G（τ）≠0。

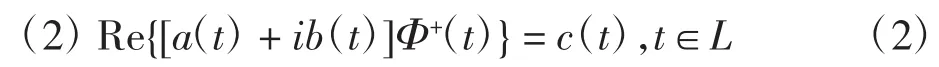
式中：a（t）、b（t）、c（t）为L上已给定的（实）函数，且都满足Hölder条件，a2+b2≠0。

三角形的各个顶点均为L上的第一类间断点，并要求Φ（z）在各间断点上至多有不到一阶奇异性。L上的间断点可分为特异节点和普通节点，求解时通常要求Φ（z）属于某个解类。这里规定在h（c0）解类中求解，即c0为某个普通节点，且Φ（z）只在c0上有界，在另外一个普通节点c1上至多有不到一阶的奇异性（节点c2为特异节点）。多角形也可进行类似定义，从而将全部类型节点都讨论在内（c0、c1、c2是三角形上3个顶点）。

规定指标为：

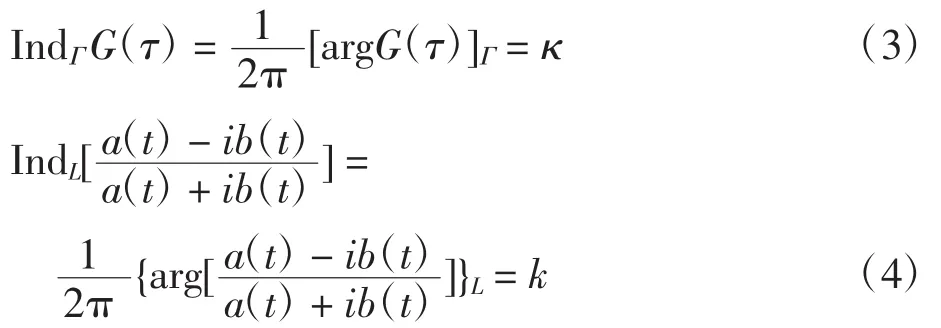
记K=2κ+k为复合边值问题的指标，注意指标不一定是偶数。

1.2 复合边值问题的转化

对于三角形域上复合边值问题，主要解决思路是通过“消去法”将其转化为相应的H问题。构造三角形内的分区全纯函数为：

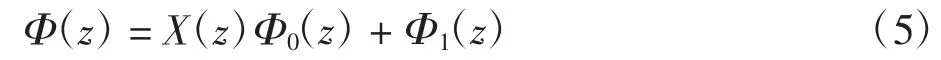
式中：Φ0（z）为G内任意连续到边界L的全纯函数；X（z）、Φ1（z）分别为满足跳跃问题式的典则函数及一般解，在这里要求连续到边界L。

z0为D-任意一点，得到通解为：

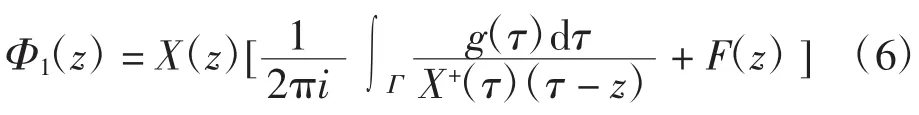
其中

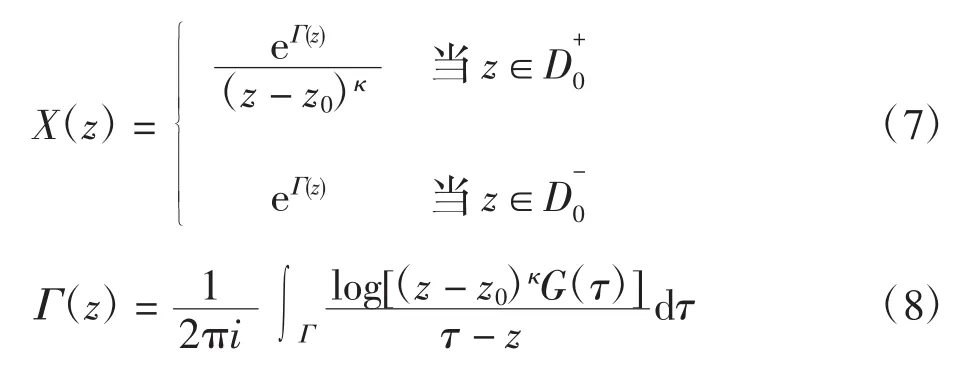
根据解析函数和典则函数的性质，容易证明：当Φ1（z）、Φ0（z）满足上述函数条件时，Φ（z）为连续到L且满足边值条件式（1）的分区全纯函数，反之同样成立。将式（5）代入式（2）得到新的H问题边值条件为：

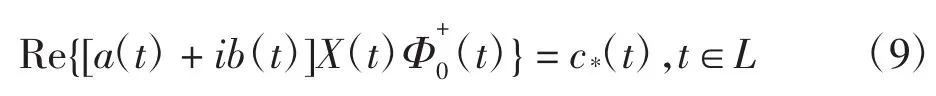
式中：c*（t）=c（t）-Re{[a（t）+ib（t）]X（t）Φ1（t）}。显然，X（t）、c*在L上满足Hölder条件。原RH问题转化为G中新H边值问题（称新H问题为H*问题），即在G中求全纯函数Φ0（z），使该函数满足新H问题边值条件式（9）。根据构造的式（5），消去繁琐函数便求得Φ（z）。

2 单位圆与三角形区域之间的共形映射

通过消去法，三角形区域上RH问题转化为H*问题，但在三角形区域上H*问题的解析解求解过程与单位圆或半平面上的情况有所不同，新的边值条件会发生改变。针对该问题，采用三角形区域到单位圆的共形映射原理，找出共形映射的函数φ（z）的具体表达式（逆变换实现了单位圆到三角形区域的共形映射），将圆域已有的结果移植到三角形区域上并求解函数表达式。根据逆变换公式，经过二次变换得出三角形区域上H*问题的解和可解性条件公式。

2.1 Schwarz-Christoffel公式

定理1 设w=f（z）为将区域I（z）＞0共形映射到多角形区域G的单叶解析函数，x轴上的点（a1＜a2＜…＜an）依次对应到G内各个顶点（w1，w2，…，wn）。以λ1π，λ2π，…，λnπ（0＜λk＜2；k=1，2，…，n）分别表示G中w1，w2，…，wn各顶点所对应的内角，则有Schwarz-Christoffel公式为：

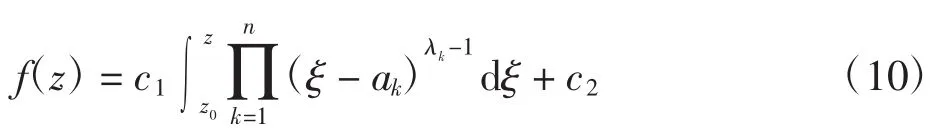
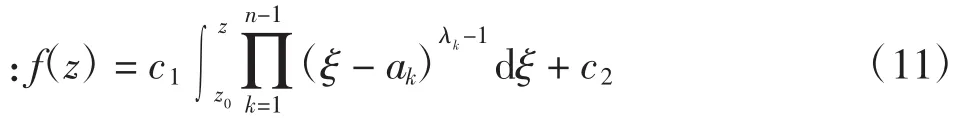
2.2 单位圆到三角形域的保形映射

由于已有半平面到多角形域为保形映射，单位圆到多角形区域的保形映射可以计算得到。这里以正三角形所围成的单连通区域为研究对象，即可给出单位圆共形映射到三角形域的单叶解析函数表达式。

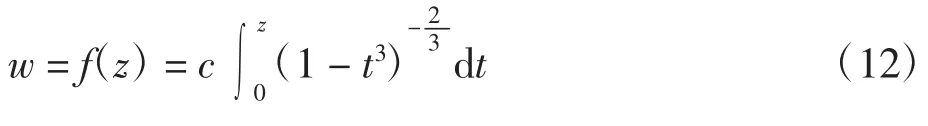
2.3 三角形区域到单位圆的保形映射

共形映射式属于Schwarz-Christoffel积分，即椭圆积分，因此用椭圆函数理论求其逆映射。

定义1

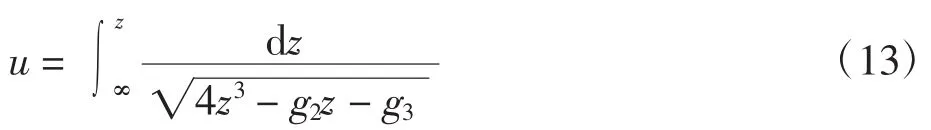
式（13）为维尔斯特拉斯式的第一类型椭圆积分，它的反函数记做z=σ（u），称维尔斯特拉斯椭圆函数，该椭圆函数有对应的级数表达。

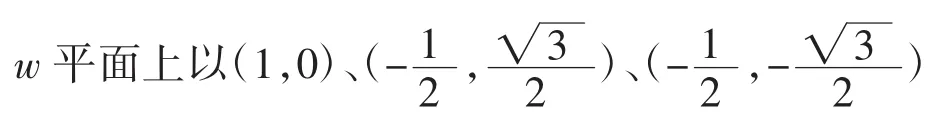
为顶点的等边三角形内部G映射到单位圆（|z|＜1）的共形映射如图2所示。表达式为：

图2 三角形到圆域的映射

魏尔斯特拉斯椭圆函数的级数展开式为：

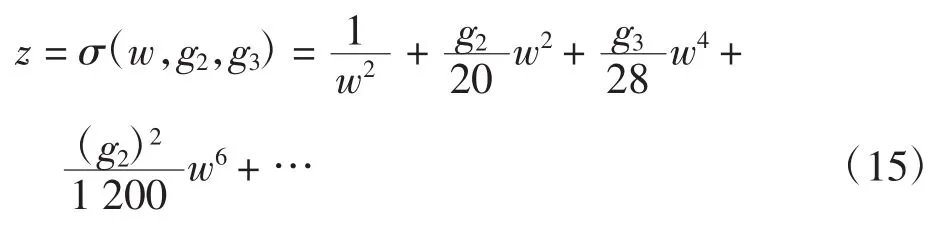
从而容易推断出这个变换公式的二阶级点为w=0、零点为w=∞。

3 单位圆域上的H*问题

在前文三角形区域与单位圆域之间共形映射的基础上，根据单位圆上H*问题的相关结果，可得出三角形区域上的解析解和可解条件公式。但H*问题与以往闭合曲线的情况不同，是带间断系数的H*问题。

为表达清晰，仍延用第一节中函数符号Φ0（z）和变量t、边值条件式（9）、单位圆边界记号L及对间断点的要求，但将3个顶点记号变为z0、z1、z2。式（9）中的实函数作用于共形映射t=f（v）（这里v为圆周上任意一点，t=f（v）为单位圆到三角形域的变换）之后，其形式也会变化。例如，a（t）变换为a（f（v））。为方便统一记为a（f（v））=a（t），其他实函数也如此定义，如图3所示。

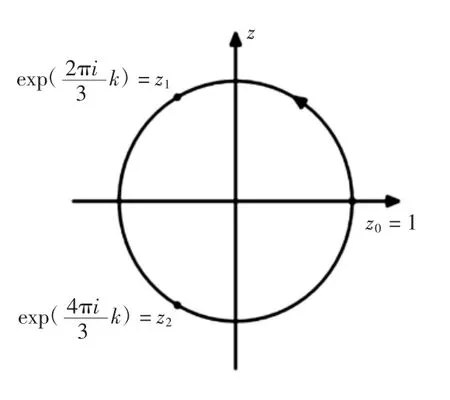
图3 单位圆上的H*问题

求解H*问题的基本思路为：将添加一些特定的附加边值条件的H*问题化为熟知的R问题。

3.1 指标和典则函数的说明

把Φ0（z）对称扩张为复平面上分区全纯函数，为方便仍记为Φ0（z），即在全平面内除了L上的点，处处都有

这个条件称为附加条件。

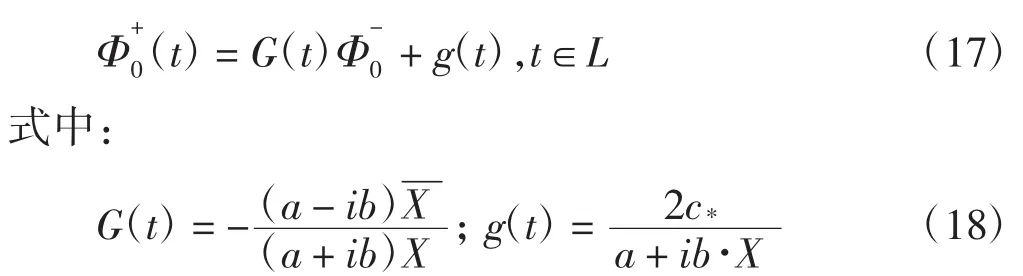
对节点进行讨论。与第一节对应，z0为普通节点，且在该点处Φ0（z）有界，其他节点只要求有不到一阶奇异性，3个点为G（t）、g（t）的第一类间断点，且它们在L上都属于H0类。

Γ（z）在L上为单值连续，IndLX（t）=-κ+IndLeΓ(z)= -κ，故R边值问题的指标为：

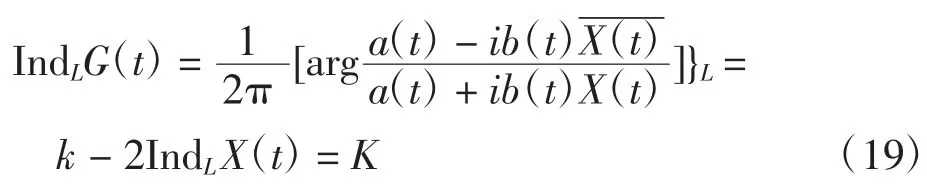
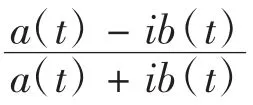
在h（z0）解类下的指标与典则函数，要根据普通节点和特异节点分布情况来定义。设由z0、z1确定的弧为L1，逆时针方向依次为L2、L3，每一个弧上任意取定l ogG（t）某一单值连续分支，，式中正负号的取值取决于在弧段中是起点还是终点。

设L1内非节点的点z*为一特异节点，易得h（z0）解类中的指标为：

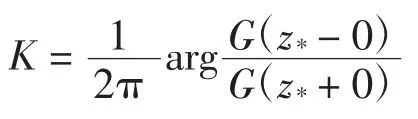
数值上与原复合边值问题的指标相等。

相应的典则函数改写为：

3.2 H*边值问题的求解

（1）齐次问题（c*≡0）

①当K≥0时，相应的R0问题一般解为：

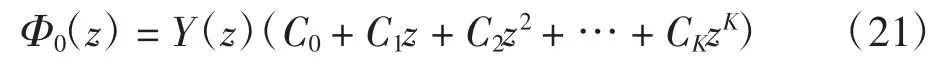
式中：C0、C1、…、CK为任意常数。

Φ0（z）要满足附加条件，根据，得到

②当K≤-1时，只有零解。

（2）非齐次问题（c*≠0）

①当K≥0时，特解为：通解为特解式（22）加上一般解式（21）。

②当K=-1时，有唯一解，即为特解。化解为：

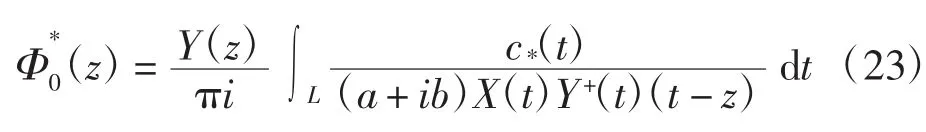
③当K≤-2时，当且仅当满足条件

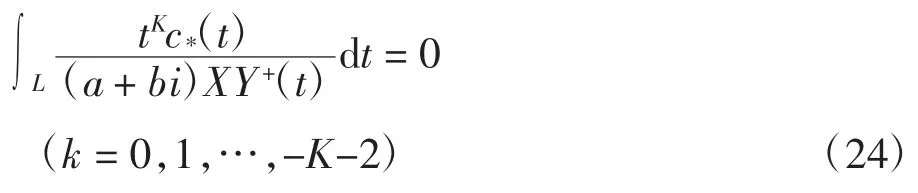
有唯一解式（23）。

3.3 原RH问题的解析解形式

单位圆上带间断系数H*的问题解决之后，通过单位圆到三角形区域的共形映射，易得三角形区域上对应的H*问题的解和可解条件公式。本文做了2次互逆的共形映射，最终实函数a（t）、b（t）、c（t）、c*（t）、X（t）、Γ（z）可沿用原记号。整理三角形域上带间断系数的RH问题的解析解形式。

（1）原RH问题中的g（τ）≡0、c（t）≠0，称这个情况为真齐次问题。

①当K≥0时，原RH问题的一般解为：

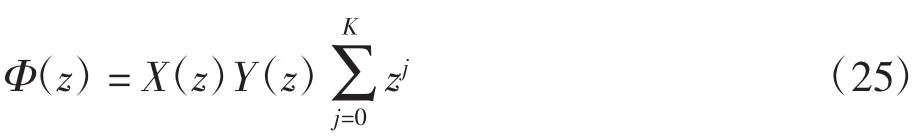
②当K＜0时，H*问题只有零解，故原RH问题也只有零解。

（2）原问题中的g（τ）≡0、c（t）=c*（t）≠0，即H*问题是非齐次的，称真非齐次问题。

①当K≥0时，

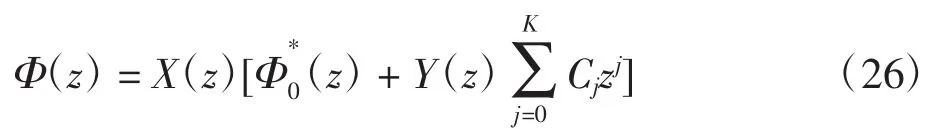
②当K＜0且条件式（24）成立时，相应R问题式（17）在R0中有唯一解，则原复合边值问题也有唯一解式（26）。

（3）原问题中的g（τ）≠0，则Φ1（z）≠0，此时分2种情况。

2K＞0时，原RH问题一般解式（26）右边还需加上Φ1（z）。

2K＜0时，仅当实函数满足-2K-1个实条件时，才有唯一解，即式（26）加上Φ1（z）。

K≥0时，原RH问题的一般解为式（25）右边加上Φ1（z）。

K＜0时，由于相应的H*问题只有零解，故原RH问题有非零唯一解Φ1（z）。

定理2（三角形区域上的RH问题）

当K≥0时，RH问题恒有解，且由K+1的实常数决定。

当K＜0时，对于真齐次问题，只有零解；对于准齐次RH问题，有非零唯一解Φ1（z）；对真非齐次RH问题，仅当已知的实函数都满足相应的-2K-1个实条件时，才有唯一解。

4 结束语

针对单位圆域到多角形区域上的共形变换，特别以正三角形为例，采用共形映射、椭圆函数理论方法和相关数学软件，完整求解变换的表达式。所求得的变换表达式是通用表达式，可直接应用在力学计算中。此外，还分析带间断点的RH问题在不同节点的求解情况，得到解决一般RH问题的常用思路，最终给出三角形区域上RH问题的解析解。整个求解思路可以移植到其他带间断点闭合曲线上，进而快速求解相应的RH问题。

［1］ 路见可.解析函数边值问题教程［M］.武汉：武汉大学出版社，2009.

［2］ LU J K.On compound boundary problem［J］.Science Sinica，1965，14（11）：1545-1555.

［3］ 张霞，李星.非正则型复合边值问题［J］.宁夏大学学报：自然科学版，2002，23（3）：193-197.

［4］ GUO D J.Multiple positive solutions for first order impulsive singular integro-differential equation on the half line［J］.Acta Mathematica Scientia：Series B，2012，32（6）：2176-2189.

［5］ 路见可.平面弹性周期问题概论［M］.武汉：武汉大学出版，2008.

［6］ 李星，路见可.双周期弹性断裂理论［M］.北京：科学出版社，2015.

［7］ 李星.一类周期裂纹问题的数值解［J］.宁夏大学学报：自然科学版，1998，19（1）：45-46.

［8］ LI X.Complex analytic methods in mechanics［J］.Joumal of Ningxia University：Natural Science Edition，2001，22（3）：272-273.

［9］ 李星，霍华颂，时朋朋.一维六方压电准晶对称条形体中共线双半无限快速传播裂纹的解析解［J］.固体力学学报，2014，35（2）：135-136.

［10］BEGEHR H，WEN G C.Nonlinear Elliptic Boundary Value Problems and Their Applications［M］.Harlow：Longman，1996.

［11］LIN J，DU J Y.Stability of displacement of the second fundamental problem in plane elasticity［J］.Acta Mathematica Scientia：Series B，2014，34（1）：125-140.

［12］DUAN P，DU J Y.Riemann-Hilbert characterization for main bessel polynomials with varying large negative parameters［J］. Acta Mathematica Scientia：Series B，2014，34（2）：557-567.

［13］闻国椿.共性映射与边值问题［M］.北京：高等教育出版社，1985.

［14］普利瓦洛夫．复变函数引论［M］．闵嗣鹤，等译.哈尔滨：哈尔滨工业大学出版社，2013.

On triangular compound boundary problem

HU Jie，LIU Hua
（School of Science，Tianjin University of Technology and Education，Tianjin 300222，China）

In view of the compound boundary value problem on the triangle region，the solution of the problem is solved by using the method of problem solving.Schwarz-Christoffel formula is used to give the conformal mapping from circular domain to triangle region，further by using elimination to change the composite boundary value problem into the Hilbert boundary value with discontinuous coefficients.By analytic continuation of the problem with discontinuous coefficients，the analytical solution of the composite boundary value problem is obtained.

schwarz-christoffel'formula；elliptical function；plemelj formula；compound boundary value problem

O175.8

A

2095－0926（2016）04－0040－05

2016-09-02

胡 洁（1991—），女，硕士研究生；刘 华（1971—），男，教授，博士，硕士生导师，研究方向为复分析及其应用.